[알고리즘][그래프] 그래프의 표현과 정의

chellchell·2020년 8월 23일
그래프
0

알고리즘 이론

목록 보기
7/11
post-thumbnail

그래프

그래프의 정의

  • 정의: 그래프 G(V,E)/G=(V,E)는 어떤 자료나 개념을 표현하는 정점(vertex)들의 집합 V(=v(G))와 이들을 연결하는 간선(edge)들의 집합 E(=E(G))로 구성된 자료구조
  • 정점(vertex/node): 여러 가지 특성을 가질 수 있는 객체
  • 간선(edge/link): 정점들 간의 관계

그래프의 종류

  • 표현하고자하는 대상에 따라 여러가지 변형된 형태가 있음

i) 정점이나 간선에 추가적 속성을 부여한 경우

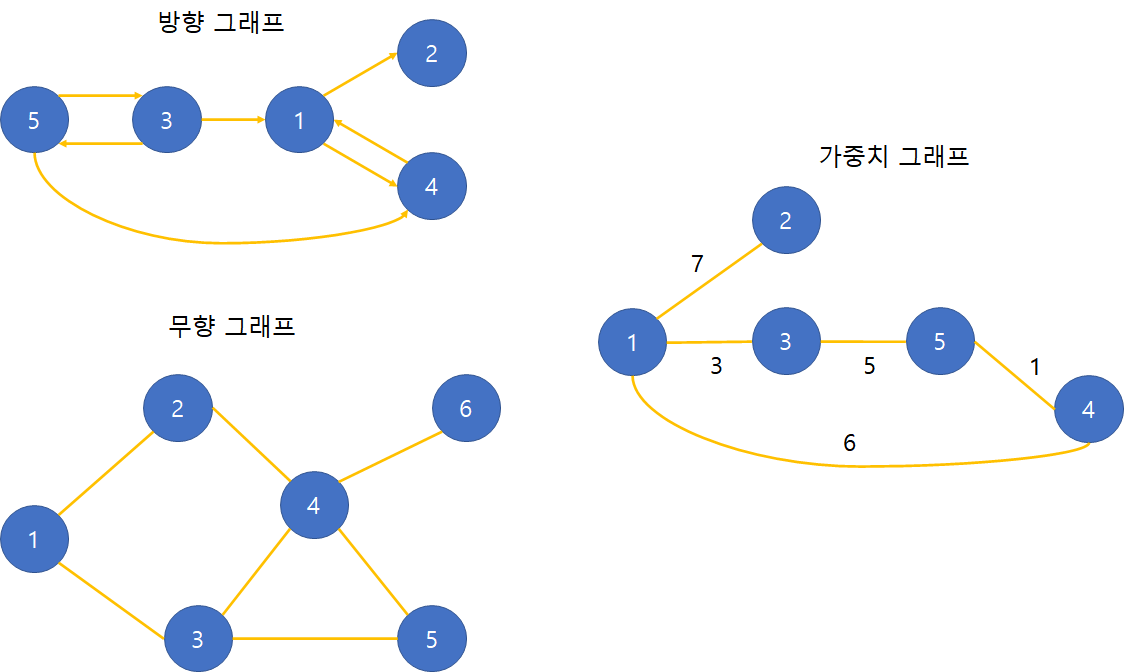
  1. 방향 그래프/유향 그래프(directed graph)

    • 각 간선이 방향이라는 속성을 갖음
    • 간선에 방향성이 존재함
    • 정점 A에서 정점 B로 가는 간선 표현법 - <A,B> ≠ <B,A>

  2. 무(방)향 그래프(undirected graph)

    • 간선에 방향이 없는 그래프
    • 양방향으로 갈 수 있음
    • 정점 A와 정점 B를 연결하는 간선 표현법 - (A,B) / (B,A)

+) 2-1. 연결 그래프(connected graph)

  • 모든 정점쌍에 대하여 항상 경로가 존재

    2-2. 완전 그래프(complete graph)

  • 그래프에 속해있는 모든 정점이 서로 연결되어 있는 그래프

  • (정점의 수) = n , (각 정점의 차수) = n-1 , (간선의 수) = nX(n-1)/2

  1. 가중치 그래프(weighted graph) / 네트워크(network)

    • 각 간선이 가중치(weight)라는 실수 속성을 갖음
    • 두 정점간의 연결 강도 나타냄

ii) 간선이나 정점의 형태에 제약을 둔 경우

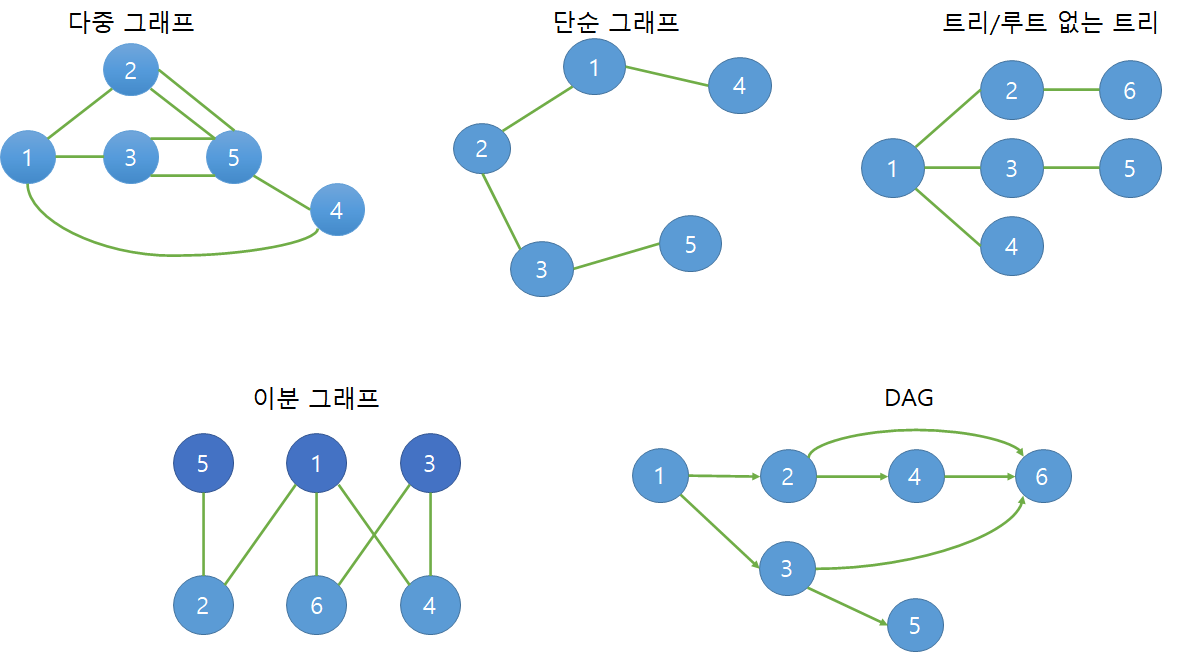
1. 다중 그래프(multigraph)

* 두 정점 사이에 두 개 이상의 간선이 있는 경우

  1. 단순 그래프(simple graph)

    • 최대 한 개의 간선만 있는 그래프

  2. 트리/루트 없는 트리(unrooted tree)

    • 부모 자식 관계가 없음
    • 무향 그래프
    • 간선을 통해 두 정점을 잇는 방법이 하나밖에 없음

  3. 이분 그래프(bipartite graph)

    • 그래프의 정점들을 겹치지 않는 두 개의 그룹으로 나눠서 서로 다른 그룹에 속한 정점들 간에만 간선이 존재

  4. 사이클 없는 방향 그래프(DAG - directed acyclic graph)

    • 두 가지 이상의 속성을 함께 가지는 경우
    • 방향 그래프
    • 한 점에서 출발해 자기자신으로 돌아오는 경로(사이클)가 존재하지 않는 경우

+) 6. 부분 그래프(subgraph)

  • 어떤 그래프의 정점의 일부와 간선의 일부로 이루어진 그래프
  • 그래프 G의 부분 그래프 S
    • v(S) ⊆ V(G)
    • E(S) ⊆ E(S)

정점의 차수

  • 인접 정점(adjacent vertex) : 간선에 의해 직접 연결된 정점

-무방향 그래프

  • 정점의 차수(degree) : 인접한 정점의 수
    • (모든 정점의 차수 합) = (간선 수) X 2

-방향 그래프

  • 진입 차수(in-degree) : 외부에서 오는 간선의 개수
  • 진출 차수(out-degree) : 외부로 향하는 간선의 개수

그래프의 경로

  • 정의: 끝과 끝이 서로 연결된 간선들을 순서대로 나열한 것
  • 단순 경로(simple path): 한 정점을 최대 한 번만 지나는 경로
  • 사이클(cycle)/회로: 시작한 점에서 끝나는 경로
  • 정점 s로부터 정점 e까지의 경로
    • 무방향 그래프 - (s,v1), (v1,v2),...,(vk,e)
    • 방향 그래프 - <s,v1>,<v1,v2>,...,<vk,e>

그래프의 사용 예

1. 철도망의 안정선 분석

  • 문제:
    어떤 철도망에서 한 역이 폐쇄되어 열차가 지나지 못할 경우 철도망 전체가 두 개 이상으로 쪼개질 가능성이 있는지, 있다면 어느 역이 그런 위험성을 갖고 있는지 분석

  • 정점:
    철도의 각 역

  • 간선:
    두 역 사이를 연결하는 철로

  • 관련 알고리즘:
    절단점 찾기 알고리즘

2. 소셜 네트워크 분석

  • 문제:
    소셜 네트워크를 통해 사람들 간의 지인/친밀도 관계를 파악할 수 있음. 이를 통해 한 다리 건너 알고 있는 사람은 몇 명이나 되는지, 몇 다리나 건너가야 누군가와 내가 아는 사이인지 알 수 있음

  • 정점:
    소셜 네트워크 사이트의 회원

  • 간선:
    두 회원이 서로 친구 사이인 경우 연결

  • 관련 알고리즘:
    그래프의 너비 우선 탐색

3. 인터넷 전송 속도 계산

  • 문제:
    어떤 경로의 시간당 전송 용량은 이 경로가 지나는 케이블 중 가장 작은 전송 용량을 갖는 케이블에 의해 좌우됨. 이때 두 컴퓨터 간의 전송 용량 계산

  • 정점:
    인터넷에 연결된 라우터와 컴퓨터

  • 간선:
    두 기계를 연결하는 케이블

  • 관련 알고리즘:
    최소 스패닝 트리 알고리즘

4. 한 붓 그리기

  • 문제:
    종이에서 연필을 떼지 않고 주어진 도형을 그리되, 모든 선을 한 번씩만 지날 수 있는지. 즉, 모든 간선을 한 번씩만 지나는 경로를 찾을 수 있는지.

  • 정점:
    선들이 만나는 점

  • 간선:
    점들을 연결하는 선

  • 관련 알고리즘:
    오일러 경로(Eulerian path), 깊이 우선 탐색

5. 외환 거래

  • 문제:
    외환 거래 시장은 달러, 유로, 엔, 스위스 프랑 등의 통화(currency)와 이들 간의 교환 비율로 구성됨. 1달러를 들고 유로로 바꾸고, 유로를 엔으로 바꿨다가, 다시 달러로 바꿨을 때 1달러보다 많은 돈을 가지게 되는 것을 아비트러지(arbitrage)라고 함. 환율 목록이 주어질 때 아비트러지가 존재하는지 여부
    +) 아비트러지가 있다 ⇔ 간선 가중치의 합이 음수인 사이클이 있다

  • 정점:
    통화

  • 간선:
    서로 교환 가능한 통화들 사이에 (방향이 있는) 간선

  • 관련 알고리즘:
    최단 거리 알고리즘

암시적 그래프 구조들

  • 그래프 같은 형태를 갖는 구조가 아니라도 그래프를 통해 표현하면 쉬운 문제
  • 암시적 그래프(implicit graph)

할 일 목록 정리

  • 문제:
    의존 관계에 있는 여러 할 일이 있을 때 이들을 한 번에 하나씩 해나갈 방법이 있는지, 있다면 어느 순서대로 하면 되는지 계산

  • 관련 알고리즘:
    위상 정렬(topological sorting), 깊이 우선 탐색

15-퍼즐

  • 문제:
    1~15 숫자 타일을 움직여 원래 있던 순서대로 정렬하는 15-퍼즐 문제

  • 정점:
    현재 타일의 배치

  • 간선:
    한 배치에서 타일을 한 번 움직여 다른 배치를 얻을 수 있을 때 두 정점 연결

  • 관련 알고리즘:
    최단 경론 문제

게임판 덮기

  • 문제:
    정사각현의 게임판(가로,세로 길이:N)을 1X2크기의 블록으로 모든 칸을 덮는 문제

  • 정점:
    막히지 않는 각 칸

  • 간선:
    상하좌우로 인접한 칸들 사이 연결

  • 관련 알고리즘:
    이분 그래프, 이분 매칭 그래프

회의실 배정

  • 문제:
    N개의 팀이 회의를 하려고 하는데, 회의실이 하나뿐인 관계로 한 번에 한 팀만 사용할 수 있음. 각 팀이 회의실을 사용하고 싶은 시간을 각각 두 개씩 적어 냈을 때 모든 팀이 회의하도록 배정하는 방법 찾기.

  • 관련 알고리즘:
    만족성 문제(satisfiability problem), 2-SAT(두 선택지 중 하나를 선택해야 하는 문제), 강 결합성 문제

그래프의 표현 방법

  • 새로운 정점이나 간선을 추가하고 삭제하는 일이 자주 발생하지 않음
  • 간단하고 메모리를 적게 차지하는 방법으로 구현
  • 정점:
    0부터 시작하는 번호 부여, 배열에 각 정점의 정보를 저장
  • 간선:
    반대쪽 끝 정점의 번호 저장
  • 간선의 정보를 어떤 식으로 저장하느냐에 따라 두가지로 나뉨
    • 메모리나 시간 사용 특성이 다름

1. 입접 리스트 표현

  • 인접 리스트(adjacency list): 그래프의 각 정점마다 해당 정점에서 나가는 간선의 목록을 저장
  • 각각의 정점에 인접한 정점들을 연결 리스트로 표현

각 정점마다 하나의 연결 리스트를 갖음

vector <list<int>> adjacent;

adjacent[i] : 정점 i와 간선을 통해 연결된 정점들의 번호 저장

#define MAX_VERTICES 50
typedef struct GraphNode{
int vertex;
struct GraphNode *link;
} GraphNode;
typedef struct GraphType{
int n;//정점의 개수
GraphNode * adj_list[MAX_VERTICES];
}GraphType;

간선이 추가적 속성을 갖고 있음

//1. 간선의 정보를 구조체로 표현
struct Edge{
int vertex;
int weight;
};
//2. 단순하게 pair 사용
pair<int,int>

2. 인접 행렬 표현

  • 인접 행렬(adjacency matrix): |V| X |V| 크기의 행렬, 즉 2차원 배열을 이용해 그래프의 간선 정보를 저장

2차원 불린 값 배열

vector<vector<bool>> adjacent;

adjacent[i,j] : 정점 i에서 정점 j로 가는 간선이 있는지를 나타내는 불린 값 변수

#define MAX_VERTICES 50
typedef struct GraphType{
int n;//정점의 개수
int adj_mat[MAX_VERTICES][MAX_VERTICES];
} GraphType

무방향 그래프 - 간선 삽입 시 adj[start][end]와 adj[end][start]에 1 삽입
방향 그래프 - 간선 삽입 시 adj[start][end]에만 1삽입

간선이 추가적 정보를 갖고 있음

vector<vector<int>> adjacent;
vector<vector<double>> adjacent;

두 정점 사이에 간선이 없을 경우 -1 또는 아주 큰 값 등 존재할 수 없는 값으로 지정

3. 인접 행렬과 인접 리스트 비교

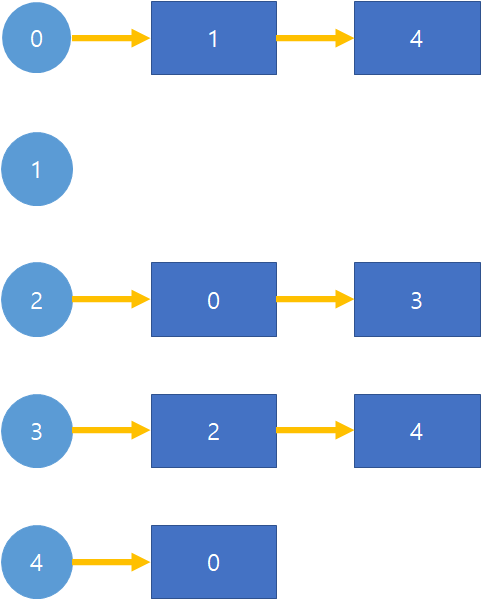
-인접 리스트

  • 장점: 실제 간선 수만큼의 원소 O(∣V∣+∣E∣|V| + |E|)의 공간만을 사용
  • 단점: 정점의 번호 u,v사이의 간선이 있는지 여부를 연결리스트 adjacent[u]를 처음부터 일일이 확인해야함
  • 희소 그래프(sparse graph): 간선의 수가 ∣V∣2|V|^2 에 비해 훨씬 적은 그래프 → 인접 리스트 사용

-인접 행렬

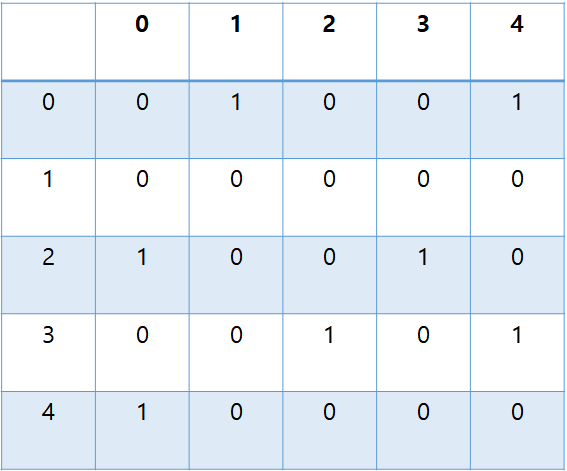
  • 장점: 한 번의 배열 접근만으로 정점의 번호 u,v사이의 간서이 있는지 여부 확인 가능
  • 단점: 항상 O(∣V∣2|V|^2)크기의 공간을 사용함
  • 밀집 그래프(dense graph): 간선의 수가 ∣V∣2|V|^2 에 비례하는 그래프 → 인접 행렬 사용
profile
chellchell
high hopes
이전 포스트

[알고리즘][정렬] 퀵 정렬

다음 포스트

[알고리즘][그래프] 그래프 추상 데이터 타입의 구현

0개의 댓글