AI Math

딥러닝 학습방법 이해하기

신경망의 이해 및 softmax 연산

• 신경망(Neural Network)는 비선형 모델이지만, 수식적으로는 선형 모델이 숨겨져있으며, 선형모델과 비선형 함수의 결합임.
• 출력벡터 $o$에 softmax 함수를 합성할 경우 확률벡터가 됨
  -> 특정 클래스 $k$에 속할 확률로 해석하여 분류문제(주어진 데이터가 특정 클래스에 속하는 지를 판단하는 문제)를 풀 때 사용할 수 있음
  $\mathrm{softmax(o)}=\Bigg(\frac{\mathrm{exp(o_1)}}{\sum_{k=1}^{p}\mathrm{exp(o_k)}}, ... , \frac{\mathrm{exp(o_p)}}{\sum_{k=1}^{p}\mathrm{exp(o_k)}} \Bigg) = \mathrm{softmax(Wx+b)}$

  def softmax(vec):
      denumerator = np.exp(vec - np.max(vec, axis=-1, keepdims=True))
      numerator = np.sum(denumerator, axis=-1, keepdims=True)
      val = denumerator / numerator
      return val
  '''
  array([[2.44728471e-01, 6.65240956e-01, 9.00305732e-02],
         [9.00305732e-02, 2.44728471e-01, 6.65240956e-01],
         [2.06106005e-09, 4.53978686e-05, 9.99954600e-01]])
  '''

• 추론(Inference)을 할 때에는 One-hot Vector(최대값을 가진 주소만 1로 출력하는 연산)를 사용해서 softmax를 사용하진 않음

  def one_hot(val, dim):
      return [np.eye(dim)[_] for _ in val]
  
  def one_hot_encoding(vec):
      vec_dim = vec.shape[1]
      vec_argmax = np.argmax(vec, axis=1)
      return one_hot(vec_argmax, vec_dim)
  
  def softmax(vec):
      denumerator = np.exp(vec - np.max(vec, axis=-1, keepdims=True))
      numerator = np.sum(denumerator, axis=-1, keepdims=True)
      val = denumerator / numerator
      return val
  
  vec = np.array([[1, 2, 0], [-1, 0, 1], [-10, 0, 10]])
  print(one_hot_encoding(vec))
  print(one_hot_encoding(softmax(vec)))
  '''
  [array([0., 1., 0.]), array([0., 0., 1.]), array([0., 0., 1.])]
  [array([0., 1., 0.]), array([0., 0., 1.]), array([0., 0., 1.])]
  '''

활성함수와 역전파(Back Propagation) 알고리즘

활성함수

• $\Reals$ 위에 정의된 비선형 함수로서, 선형모형과 딥러닝을 구분해주는 가장 중요한 개념
• 대표적인 12 종류의 활성함수 (출처: V7 Labs)
  
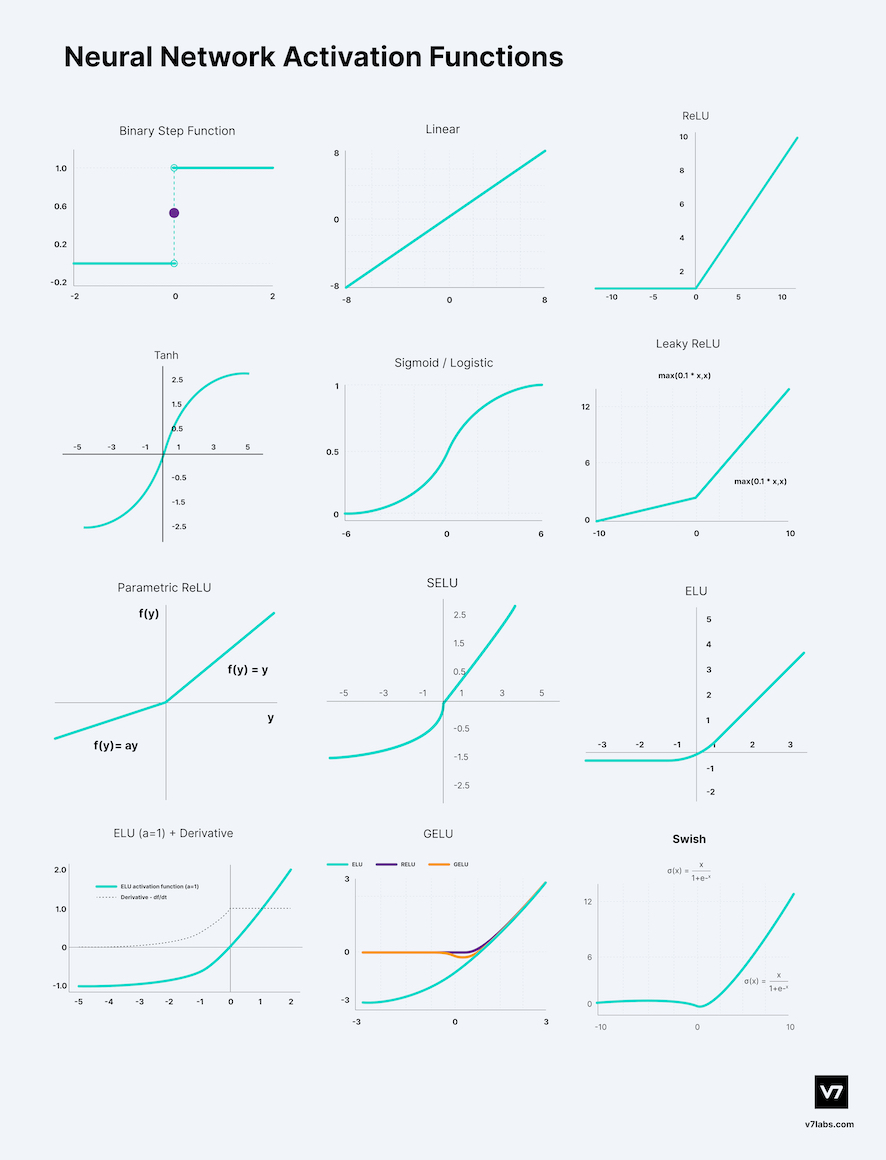
• 현재의 딥러닝에서는 ReLU 함수가 많이 쓰이지만, 과거에는 시그모이드(sigmoid; $\sigma$)나 하이퍼볼릭 탄젠트(Hyperbolic Tangent; $tanh$)가 많이 쓰였으며, sigmoid, tanh의 미분 그래프는 아래와 같음
  

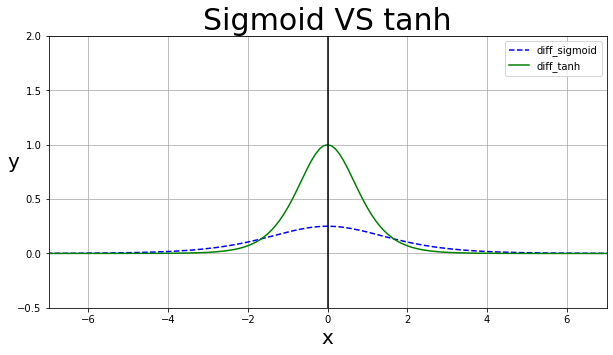
다층 퍼셉트론(Multi-Layer Perceptron; MLP)

• MLP는 신경망이 여러층 합성된 함수로, 층 수 만큼의 가중치(Weight) 행렬이 존재하고, 1부터 L까지의 순차적 신경망 계산을 순전파(Forward Propagation)이라고 함.
• 이론적으로는 2층 신경망으로 임의의 연속함수에 근사할 수 있으나, 층이 깊을수록 목적함수를 근사하는데 필요한 뉴런(노드)의 숫자가 빠르게 줄어들기 때문에 효율적으로 학습이 가능함.
  (하지만 최적화는 더 어려워지는 경향이 있음)

역전파(Back Propagation) 알고리즘

• 딥러닝은 역전파 알고리즘을 이용하여 각 층에 사용된 파라미터 $\{W^{(\mathscr{l})}, b^{(\mathscr{l})}\}_{\mathscr{l}=1}^L$를 학습함.

• 경사하강법을 적용해서 각각의 가중치 행렬을 학습시킬 때, 각각의 Gradiant Vector를 계산해야함.

• 딥러닝에서는 각 층에 존재하는 파라미터에 대한 미분을 계산하여 파라미터를 업데이트
  -> 모든 행렬들의 원소들에 대하여 경사하강법 적용
  => 훨씬 많은 파라미터들에 경사하강법이 적용됨

• 각 층 파라미터의 Gradient Vector는 윗층부터 역순으로 계산(미분)하게 되며, 연쇄법칙(Chain Rule)을 통해 해당 Gradient Vector를 전달함.

연쇄법칙(Chain Rule)

• 합성함수를 미분하는 방법으로, 역전파 알고리즘은 연쇄법칙 기반 자동미분(Auto Differentiation)을 사용함.
  $z=(x+y)^2$ 이고, $z=w^2$, $w=x+y$일 때, $\cfrac{\partial{z}}{\partial{x}}$를 구하기 위해 $\cfrac{\partial{z}}{\partial{w}}\cfrac{\partial{w}}{\partial{x}}$로 각 분자, 분모에 $\partial{w}$를 곱한 뒤 분리하여 미분
  -> $\cfrac{\partial{z}}{\partial{x}}=\cfrac{\partial{z}}{\partial{w}}\cfrac{\partial{w}}{\partial{x}}=2w*1=2(x+y)$

회고

• 앞서 배웠던 것들이 종합되며 딥러닝과 연관되는 부분이라 집중해서 들었다.
• 분명히 Gradient Vector 관련 설명을 이해했었다고 생각했는데, 이 부분에 들어와서 다시 떠올려보니 그 개념이 맞았나? 하는 생각이 문득 들었다.
• 결국 역전파 알고리즘은 상위 층에서부터 최하층까지 역순으로 타고 내려가며 기울기 벡터를 전달한다는 의미로 이해하게 되었는데, 과연 이게 정확한 표현일까 싶다..