B+Tree란 ?
기존의 B-Tree는 어느 한 데이터의 검색은 효율적이지만 모든 데이터를 한 번 순회하는 데에는 트리의 모든 노드를 방문해야하므로 비효율적이다. 이러한 B-Tree의 단점을 개선시킨 자료구조가 B+Tree이다.
B+Tree는 오직 leaf node에만 데이터를 저장하고 leaf node가 아닌 node에서는 자식 포인터만 저장한다. 그리고 leaf node끼리는 Linked list로 연결되어 있다. 또, B+Tree에서는 반드시 leaf node에만 데이터가 저장되기 때문에 중간 node에서 key를 올바르게 찾아가기 위해서 key가 중복될 수 있다.
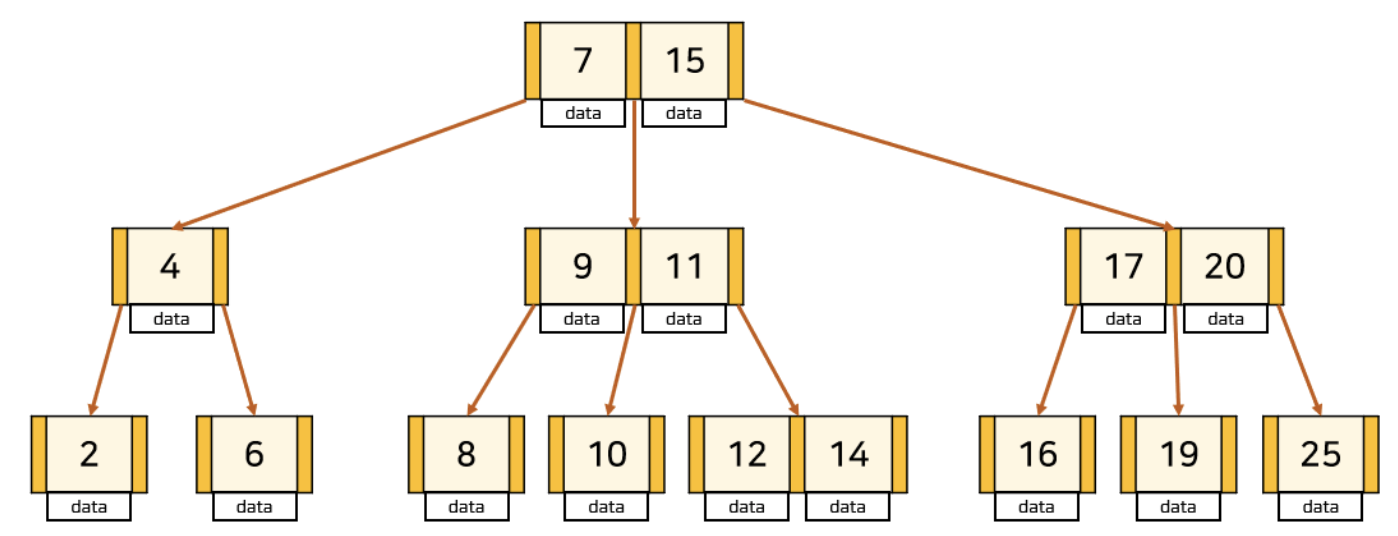
B-Tree 예시
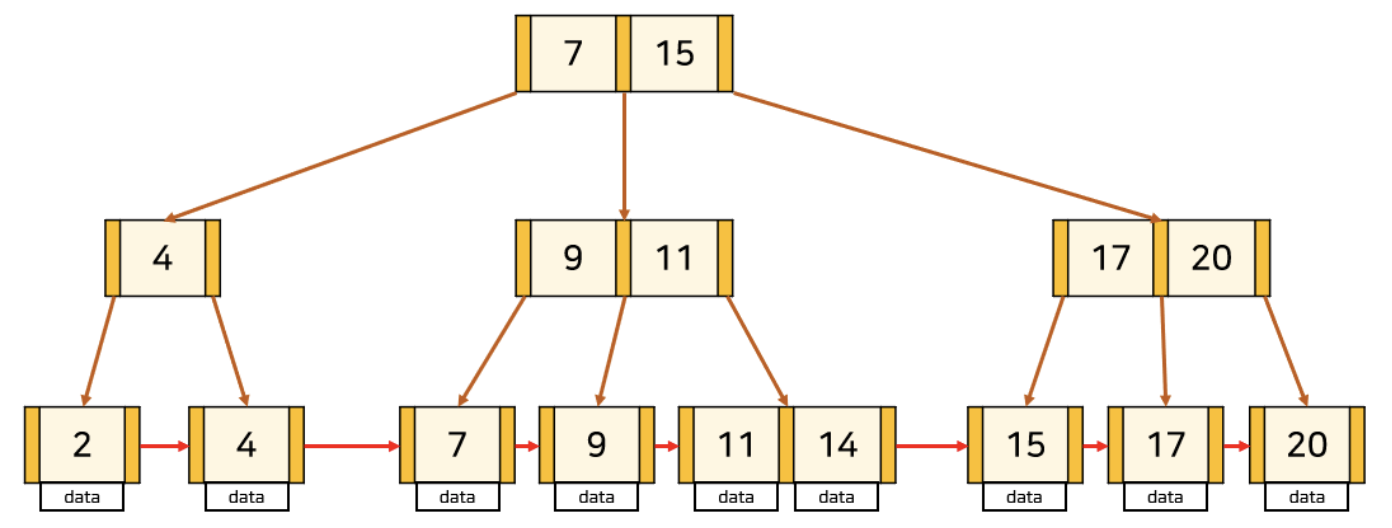
B+Tree 예시
이로 인한 장점이 뭐가 있을까 ?
1. leaf node를 제외하고 데이터를 저장하지 않기 때문에 메모리를 더 확보할 수 있다. 따라서 하나의 node에 더 많은 포인터를 가질 수 있기 때문에 트리의 높이가 더 낮아지므로 검색 속도를 더 높일 수 있다.
2. Full Scan을 하는 경우 B+Tree는 leaf node에만 데이터가 저장되어 있고 leaf node끼리 linked list로 연결되어 있기 때문에 선형 시간이 소모된다. 반면 B-Tree는 모든 node를 확인해야 한다.
반면 B-Tree의 경우 최상의 경우 특정 key를 root node에서 찾을 수 있지만 B+Tree의 경우 반드시 특정 key에 접근하기 위해서 leaf node까지 가야 하는 단점이 있다.
인덱스에서 B-Tree 대신 주로 B+Tree를 사용하는 이유는 뭘까 ?
해시 테이블에서 언급했듯이 인덱스 컬럼은 부등호를 이용한 순차 검색 연산이 자주 발생할 수 있다. 따라서 B+Tree의 Linked list를 이용하면 순차 검색을 효율적으로 할 수 있게 된다.
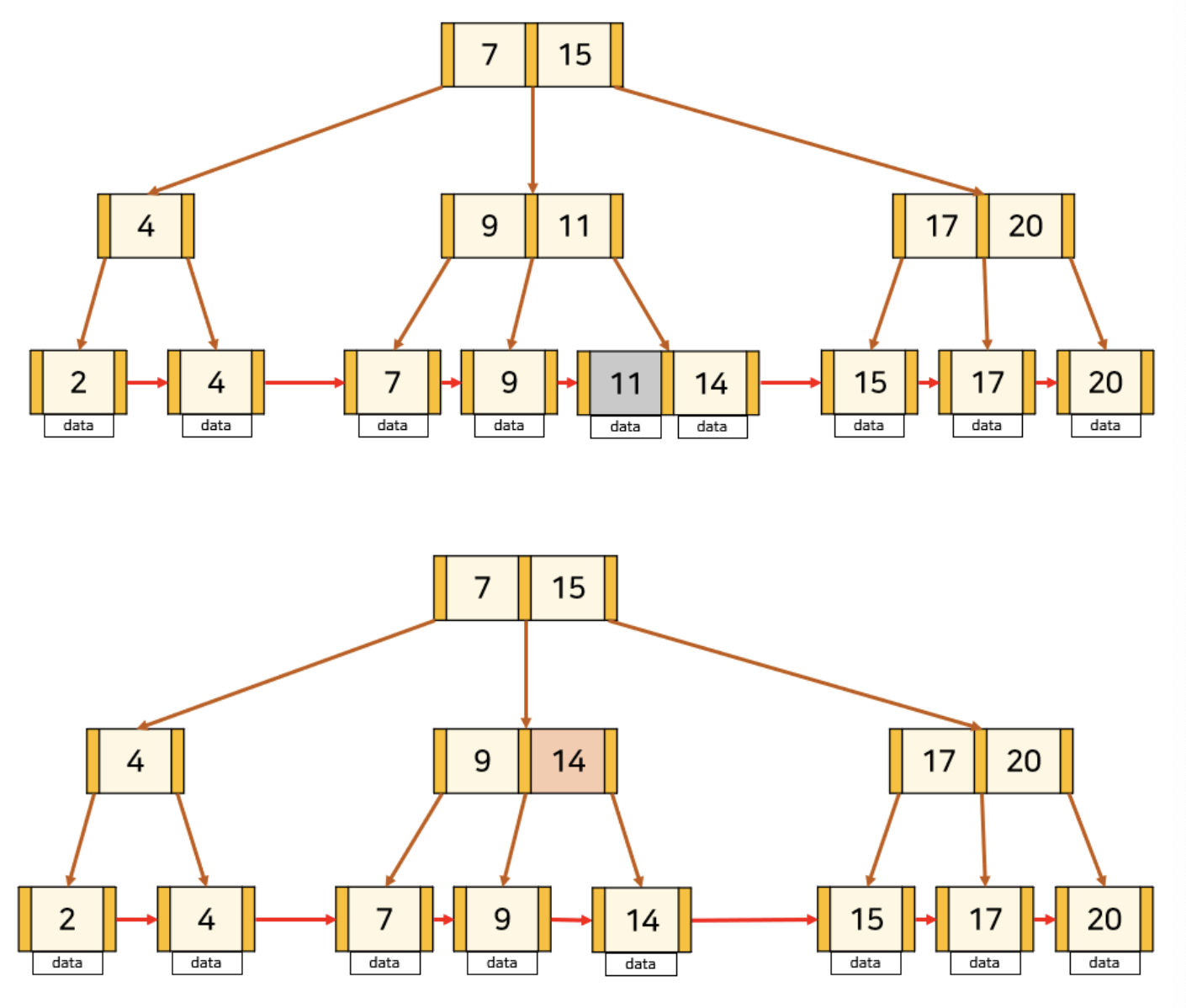
B+Tree의 검색 과정은 B-Tree와 동일하다. 반면 B+Tree의 삽입과 삭제 과정은 약간의 차이가 있다. 기본적으로 B+Tree의 삽입과 삭제는 항상 leaf node에서 일어난다.
B+Tree의 삽입
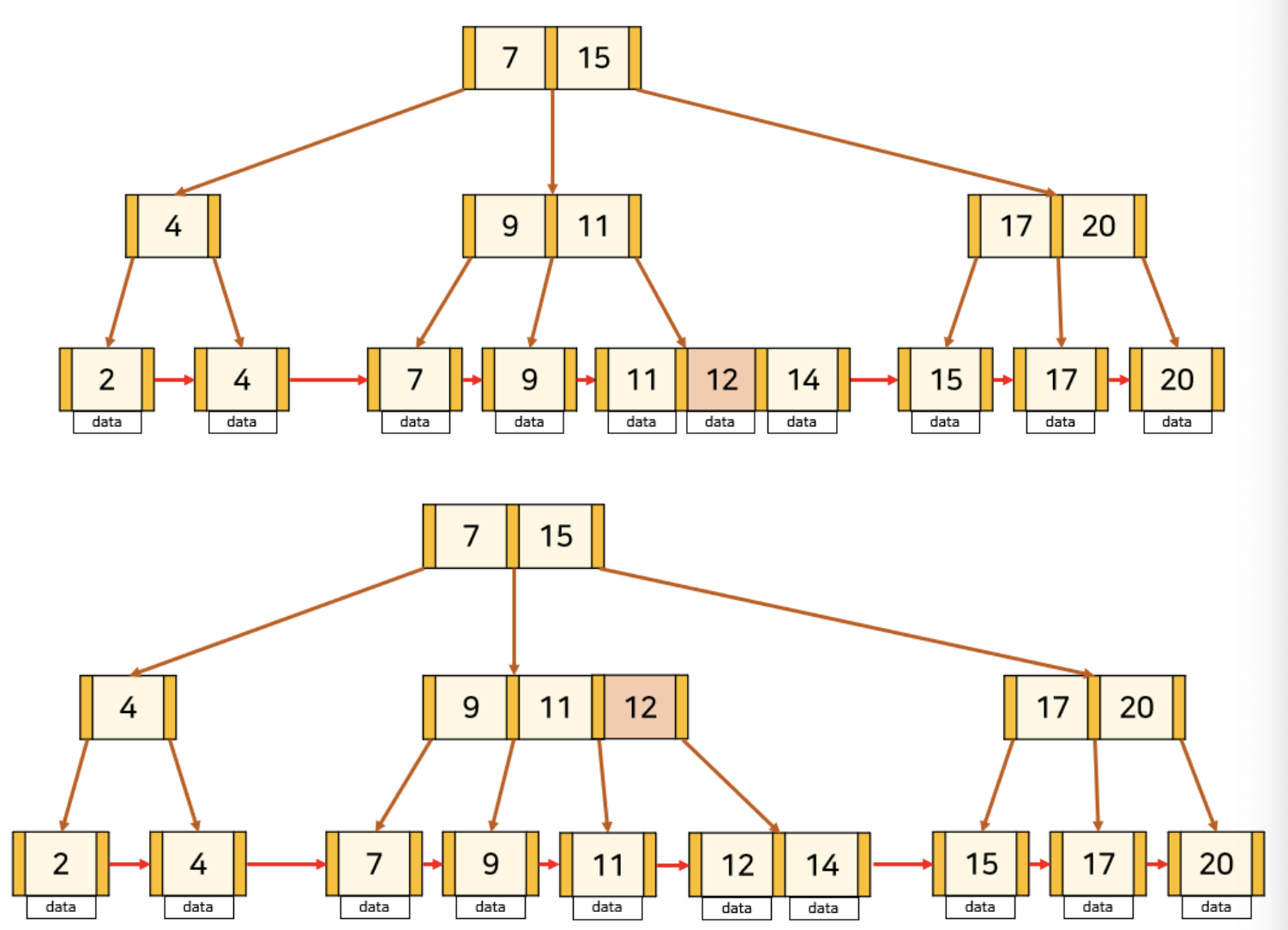
key의 수가 최대보다 적은 leaf node에 삽입하는 경우
해당 node의 가장 앞이 아닌 곳에 삽입되는 경우는 단순히 삽입해 주면 된다.
하지만, leaf node의 가장 앞에 삽입되는 경우는 해당 node를 가리키는 부모 node의 포인터의 오른쪽에 위치한 key를 K로 바꿔준다. 그리고 leaf node끼리 Linked list로 이어줘야 하므로 삽입된 key에 Linked list로 연결한다.
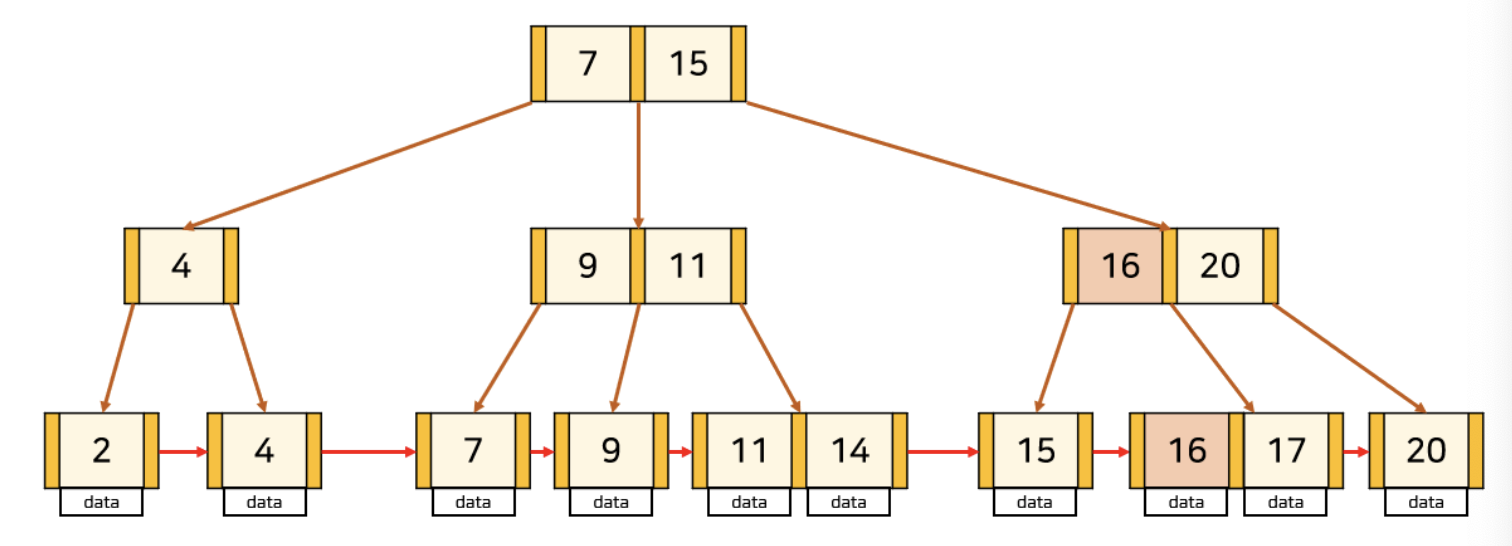
key의 수가 최대인 leaf node에 삽입하는 경우
key의 수가 최대이므로 삽입하는 경우 분할을 해주어야 한다. 만약 중간 node에서 분할이 일어나는 경우는 B-Tree와 동일하게 해주면 된다. leaf node에서 분할이 일어나는 경우는 중간 key를 부모 node로 올려주는데 이때, 오른쪽 node에 중간 key를 붙여 분할한다. 그리고 분할된 두 node를 Linked List로 연결해준다.
이후 과정은 B-Tree의 과정과 동일하다.
B+Tree의 삭제
삭제할 key가 leaf node의 가장 앞에 있지 않은 경우
B-Tree와 동일한 방법으로 삭제된다.
삭제할 key가 leaf node의 가장 앞에 위치한 경우
이 경우는 leaf node가 아닌 node에 key가 중복해서 존재한다. 따라서 해당 key를 노드보다 오른쪽에 있으면서 가장 작은 값으로 바꿔주어야 한다.