빅-오(Big-O) 표기법

빅오 표기법이란 ?

점근 표기법(asymptotic notation)은 어떤 함수의 증가 양상을 다른 함수와의 비교로 표현하는 수론과 해석학의 방법이다. 알고리즘의 복잡도를 단순화할 때나 무한급수의 뒷부분을 간소화할 때 쓰인다. 이 중 압도적으로 많이 쓰이는 것이 대문자 O 표기법, Big-O 표기법이다. 이 Big-O 표기법은 계수와 낮은 차수의 항을 제외시키는 방법이다.

알고리즘을 평가할 때 시간 복잡도와 공간 복잡도를 사용하는데 시간 복잡도는 알고리즘의 수행시간을 평가하고 공간 복잡도는 알고리즘 수행에 필요한 메모리 양을 평가합니다. 여기서 시간 복잡도와 공간 복잡도는 위와 같이 주로 점근적 표기법 중 하나인 빅오 표기법을 이용하여 나타냅니다. 빅오 표기법은 최악의 경우에도 해당 알고리즘이 어떤 성능을 낼지 가늠해볼 수 있도록 하기 때문입니다.

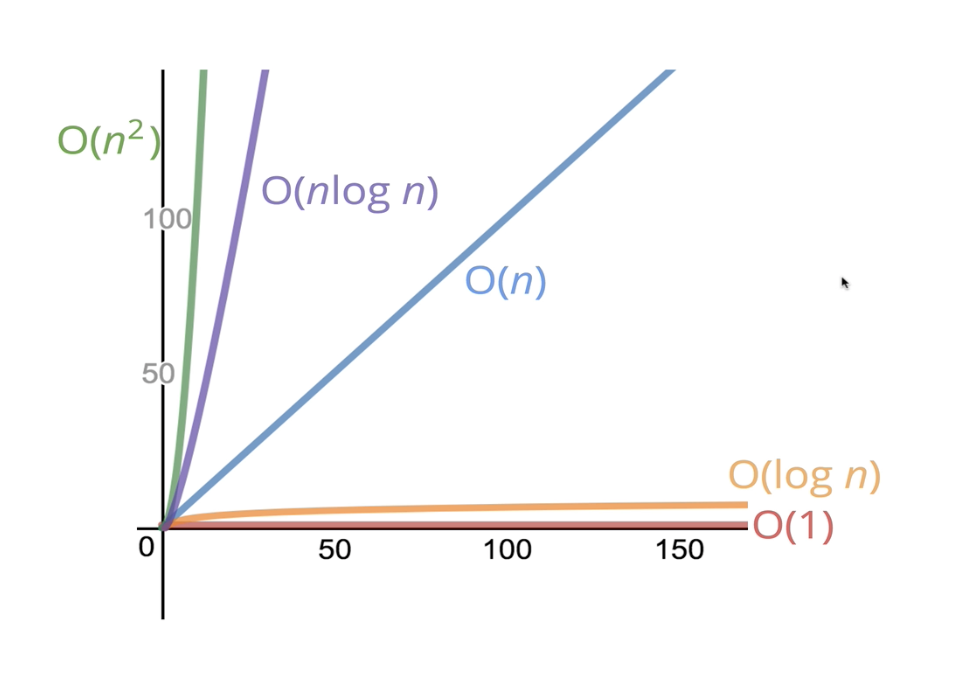
빅-오 표기법의 성능 (수행시간, 연산횟수)

O(1) < O(logn) < O(n) < O(Nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!)

수행시간이 가장 짧은 O(1)로 갈수록 성능이 좋습니다. 시간 복잡도를 낮출 수 있다면 프로그램에 큰 성능 향상을 기대할 수 있습니다.

시간복잡도

• O(1) 상수 시간: n에 상관없이 한 번에 연산만 수행한다.
• O(log n) 로그 시간: 문제를 해결하는 데 필요한 단계들이 연산마다 특정 요인에 의해 줄어든다.
• O(n) 직선적 시간: 문제를 해결하기 위한 입력 N만큼의 단계가 필요하다.
• O(Nlogn): 문제를 해결하기 위한 단계의 수가 N번에 그 하나의 N번당 필요한 단계들이 연산마다 특정 요인에 의해 줄어든다.
• O(n^2) 2차 시간: 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱
• O(2^n) 지수 시간: 문제를 해결하기 위한 단계의 수는 주어진 상수값 C의 n제곱

공간복잡도

공간 복잡도는 알고리즘에서 사용하는 메모리 양을 나타냅니다. 공간 복잡도는 보조공간(Auxiliary Space)과 입력 공간(input size)을 합친 포괄적인 개념입니다. 보조 공간(Auxiliary Space)은 알고리즘이 실행되는 동안 사용하는 임시 공간입니다. 그렇기 때문에 입력 공간(input size)을 고려하지 않습니다.

공간복잡도 예제 (javascript)

function logUpTo(n) {
  for (var i = 1; i <= n; i++) {
    console.log(i);
  }
}

공간복잡도: O(1)

function logAtMost10(n) {
  for (var i = 1; i <= Math.min(n, 10); i++) {
    console.log(i);
  }
}

공간복잡도: O(1)

function logAtMost10(n) {
  for (var i = 1; i <= Math.min(n, 10); i++) {
    console.log(i);
  }
}

공간복잡도: O(1)

function onlyElementAtEvenIndex(array) {
  var newArray = Array(Math.ceil(array.length / 2));
  for (var i = 0; i < array.length; i++) {
    if (i % 2 === 0) {
      newArray[i / 2] = array[i];
    }
  }
  return newArray;
}

공간복잡도: O(n)

function subtotals(array) {
  var subtotalArray = Array(array.length);
  for (var i = 0; i < array.length; i++) {
    var subtotal = 0;
    for (var j = 0; j <= i; j++) {
      subtotal += array[j];
    }
    subtotalArray[i] = subtotal;
  }
  return subtotalArray;
}

공간복잡도: O(n)