[LeetCode] Climbing Stairs

---

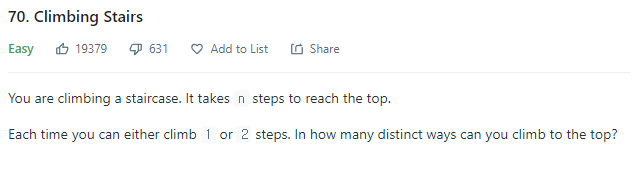
계단을 1칸 or 2칸씩 오를 수 있는데 정상까지 오르는데 n칸을 올라야 한다. 얼마나 다양한 방법으로 정상에 오를 수 있는가? 에 대한 문제이다

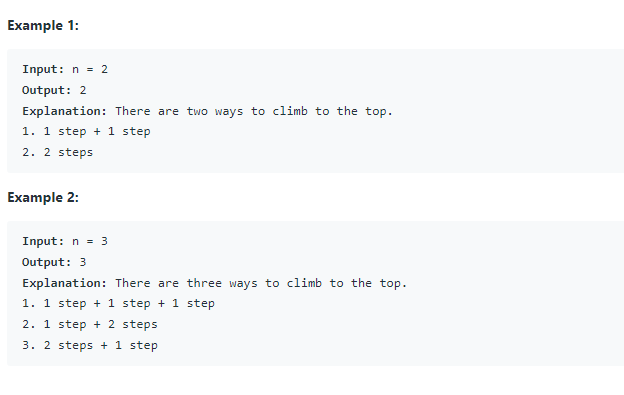
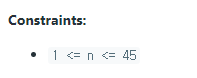
• n=2, 2ways
  (1+1,
  2)
• n=3, 3ways
  (1+1+1,
  1+2, 2+1)
• n=4, 5ways
  (1+1+1+1,
  1+1+2, 1+2+1, 2+1+1, 2+2)
• n=5, 8ways
  (1+1+1+1+1,
  1+1+1+2, 1+1+2+1, 1+2+1+1, 2+1+1+1, 1+2+2, 2+1+2, 2+2+1)
  .
  .
  .

어떻게하면 문제를 풀 수 있을까해서 일단은 n이 5일 때까지 직접 적어봤는데 어느정도 규칙은 알겠더라. 1step은 n만큼 더해진다는 것과 n이 1,2,3일 때는 'n'이 'n'ways가 성립이 되는데 4부터는 바뀐다는 점... 정도 .... ? 결국 이 문제도 검색을 해봤다 🫨.... (10에 9은 검색해보게 되는 듯한.... )

---

이 문제는 피보나치를 이용하면 간단하다고 하는데 (피보나치가 뭔데...? 그거 어떻게 하는건데...?)

class Solution {
    public int climbStairs(int n) {
        int dp[] = new int[n+1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i=2; i<=n; i++){
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }
}

class Solution {
    public int climbStairs(int n) {
        if(n==1) return 1;
        
        if(n==2) return 2;

        int[] a =  new int[n];
        a[0]=1;
        a[1]=2;

        for(int i=2;i<n;i++){
            a[i]=a[i-1]+a[i-2];
        }
        return a[n-1];
    }
}

The problem seems to be a dynamic programming one. Hint: the tag also suggests that!
Here are the steps to get the solution incrementally.

Base cases:
if n <= 0, then the number of ways should be zero.
if n == 1, then there is only way to climb the stair.
if n == 2, then there are two ways to climb the stairs. One solution is one step by another; the other one is two steps at one time.

The key intuition to solve the problem is that given a number of stairs n, if we know the number ways to get to the points [n-1] and [n-2] respectively, denoted as n1 and n2 , then the total ways to get to the point [n] is n1 + n2. Because from the [n-1] point, we can take one single step to reach [n]. And from the [n-2] point, we could take two steps to get there.

The solutions calculated by the above approach are complete and non-redundant. The two solution sets (n1 and n2) cover all the possible cases on how the final step is taken. And there would be NO overlapping among the final solutions constructed from these two solution sets, because they differ in the final step.

Now given the above intuition, one can construct an array where each node stores the solution for each number n. Or if we look at it closer, it is clear that this is basically a fibonacci number, with the starting numbers as 1 and 2, instead of 1 and 1.

The implementation in Java as follows:

public int climbStairs(int n) {
    // base cases
    if(n <= 0) return 0;
    if(n == 1) return 1;
    if(n == 2) return 2;
    
    int one_step_before = 2;
    int two_steps_before = 1;
    int all_ways = 0;
    
    for(int i=2; i<n; i++){
    	all_ways = one_step_before + two_steps_before;
    	two_steps_before = one_step_before;
        one_step_before = all_ways;
    }
    return all_ways;
}