[Array101] Basic Array Operations, Array Insertions
Basic Array Operations
Now that we have a fairly good understanding of what an Array actually is, and how it is stored inside the computer's physical memory, the next important thing to look at is all the operations that Arrays support. An Array is a data structure, which means that it stores data in a specific format and supports certain operations on the data it stores. Consider the DVD inventory management software from the introduction section. Let's look at some operations you might want to perform using this software:
- Insert a new DVD into the collection at a specific location.
- Delete a DVD from the existing collection if it doesn't make sense to keep it in the inventory anymore.
- Search for a particular DVD in the collection. This is one of the most commonly executed operation on our collection, because our inventory management software would be used hundreds of times a day to look for a particular DVD asked for by the user.
In this section, we'll be looking at the three basic operations that are supported by almost every data structure; insertion, deletion, and search.
Array Insertions
In the previous chapter, we looked at how to write elements to an Array. There is a lot more to inserting elements though, as we're about to see!
Inserting a new element into an Array can take many forms:
1.Inserting a new element at the end of the Array.
2.Inserting a new element at the beginning of the Array.
3.Inserting a new element at any given index inside the Array. Inserting at the End of an Array
At any point in time, we know the index of the last element of the Array, as we've kept track of it in our length variable. All we need to do for inserting an element at the end is to assign the new element to one index past the current last element.
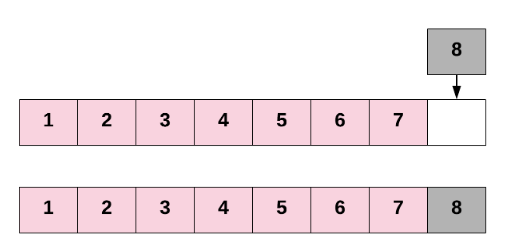
This is pretty much the same as we've already seen. Here's the code to make a new Array that can hold up to 6 items, and then add items into the first 3 three indexes.
// Declare an integer array of 6 elements
int[] intArray = new int[6];
int length = 0;
// Add 3 elements to the Array
for (int i = 0; i < 3; i++) {
intArray[length] = i;Let's define a function, printArray, to help us visualise what's happening.
for (int i = 0; i < intArray.length; i++) {
System.out.println("Index " + i + " contains " + intArray[i]);
}If we run our printArray function, we'll get the following output.
Index 0 contains 0.
Index 1 contains 1.
Index 2 contains 2.
Index 3 contains 0.
Index 4 contains 0.
Index 5 contains 0.
Notice how indexes 3, 4, and 5 all contain 0? This is because Java fills unused int Array slots with 0s.
Let's now add a 4th element. We'll add the number 10.
// Insert a new element at the end of the Array. Again,
// it's important to ensure that there is enough space
// in the array for inserting a new element.
intArray[length] = 10;
length++;Notice why we also incremented the length? It is significant to increase the length by 1. If skipping this step, next time when we add another element, we'll accidentally overwrite the one we just added!
Running printArray again, we'll get the following:
Index 0 contains 0.
Index 1 contains 1.
Index 2 contains 2.
Index 3 contains 10.
Index 4 contains 0.
Index 5 contains 0.
Inserting at the Start of an Array
To insert an element at the start of an Array, we'll need to shift all other elements in the Array to the right by one index to create space for the new element. This is a very costly operation, since each of the existing elements has to be shifted one step to the right. The need to shift everything implies that this is not a constant time operation. In fact, the time taken for insertion at the beginning of an Array will be proportional to the length of the Array. In terms of time complexity analysis, this is a linear time complexity:
O(N), where N is the length of the Array.
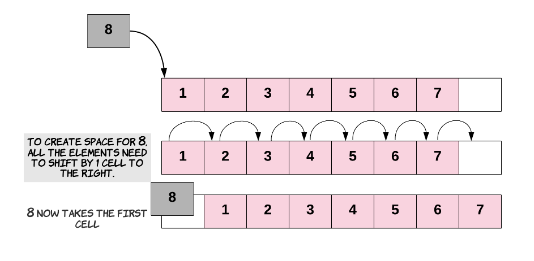
Here's what this looks like in code.
// First, we will have to create space for a new element.
// We do that by shifting each element one index to the right.
// This will firstly move the element at index 3, then 2, then 1, then finally 0.
// We need to go backwards to avoid overwriting any elements.
for (int i = 3; i >= 0; i--) {
intArray[i + 1] = intArray[i];
}
// Now that we have created space for the new element,
// we can insert it at the beginning.
intArray[0] = 20;And here's the result of running printArray.
Index 0 contains 20.
Index 1 contains 0.
Index 2 contains 1.
Index 3 contains 2.
Index 4 contains 10.
Index 5 contains 0.
Inserting Anywhere in the Array
Similarly, for inserting at any given index, we first need to shift all the elements from that index onwards one position to the right. Once the space is created for the new element, we proceed with the insertion. If you think about it, insertion at the beginning is basically a special case of inserting an element at a given index—in that case, the given index was 0.
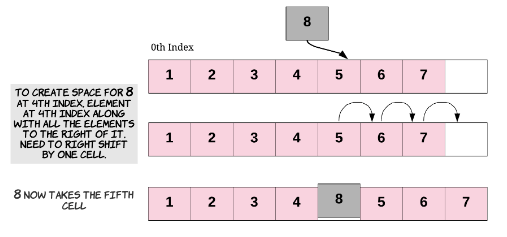
Again, this is also a costly operation since we could potentially have to shift almost all the other elements to the right before actually inserting the new element. As you saw above, shifting lots of elements one place to the right adds to the time complexity of the insertion task.
Here's what it looks like in code.
// Say we want to insert the element at index 2.
// First, we will have to create space for the new element.
for (int i = 4; i >= 2; i--)
{
// Shift each element one position to the right.
intArray[i + 1] = intArray[i];
}
// Now that we have created space for the new element,
// we can insert it at the required index.
intArray[2] = 30;And here's the result of running printArray.
Index 0 contains 20.
Index 1 contains 0.
Index 2 contains 30.
Index 3 contains 1.
Index 4 contains 2.
Index 5 contains 10.
Does that all sound good? The main thing to be careful of is remembering that array.length gives you the total capacity of the Array. If you want to know the last used slot, you'll need to keep track of this yourself using a length variable. Other than that, just be careful to read any elements you want to keep, before you overwrite them!
We now have a fun problem for you to test your understanding on. Enjoy!
잘보면 Inserting at the Start of an Array에서도 그렇고 Inserting Anywhere in the Array에서도 for 조건식에 삽입하기를 원하는 위치의 인덱스 값이 들어가고 초기화식에 배열의 끝 인덱스가 들어가면서 -를 해서 한 칸씩 이동을 한다!
