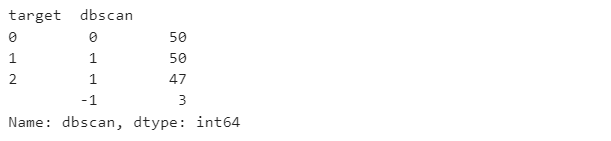사이킷런_군집화_평균이동(Mean Shift),GMM,DBSCAN

주지윤·2022년 10월 24일

사이킷런

목록 보기

21/32

2. 평균이동(MeanShift)

군집의 중심으로 지속적으로 움직이면서 군집화 수행.

KMeans와의 차이점

KMeans: 데이터의 평균거리 중심으로 이동
MeanShift: 데이터의 밀도가 가장 높은곳으로 이동

따라서, 데이터의 분포도를 이용해 군집 중심점을 찾는다. 확률 밀도 함수와 KDE(Kernel Density Estimation)를 이용

개별데이터의 특정 반경 내에 데이터 분포도를 KDE기반_MeanShift알고리즘으로 계산
KDE로 계산된 데이터가 분포도가 높은 방향으로 데이터 이동
개별데이터의 군집 중심점을 설정
지정된 반복횟수(iter)만큼 전체 데이터에 대한 KDE기반(데이터와의 거리값을 KDE함수 값으로 입력하여 반환) 데이터 이동

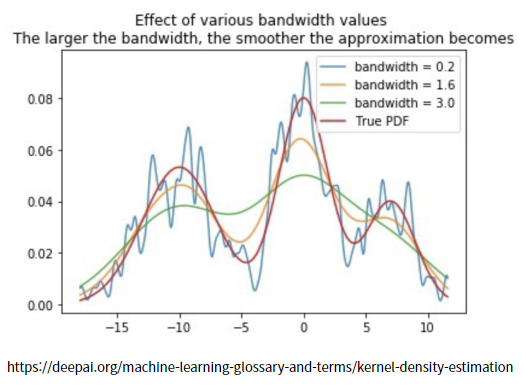
KDE란?

Kernel Density Estimation
커널함수를 통해 어떤 변수의 확률 밀도 함수를 추정

K : 커널함수
$x$ : 확률 변수값
$x_1$ : 관측값
$h$ : 대역폭(성능을 좌우)

KDE = $1\over nh$ $\displaystyle\sum_{i=0}^{n}$ ( $x-x_1\over h$ )

- 작은 h는 좁고 뾰족한 KDE → 과적합우려
- 큰 h는 과도하게 평활한 KDE → 과소적합 우려

MeanShift의 중요 파라미터

bandwidth: 대역폭 "h"
- 값을 작게할수록 군집개수가 많아짐

최적화된 bandwidth값을 찾기위한 함수: estimate_bandwidth()

1) make_blobs을 통해 MeanShift 활용

1) 데이터생성(make_blobs)

import numpy as np
from sklearn.datasets import make_blobs
X,y=make_blobs(n_samples = 200, n_features = 2, centers =3, 
               cluster_std=0.7, random_state= 0)

2) MeanShift활용

from sklearn.cluster import MeanShift

h_08 =MeanShift(bandwidth=0.8).fit_predict(X)

h_2=MeanShift(bandwidth=2).fit_predict(X)

print("h=0.8: ",np.unique(h_08, return_counts=True))
print('h=2: ',np.unique(h_2, return_counts=True))

3) 최적화된 bandwidth 찾기

from sklearn.cluster import estimate_bandwidth

bandwidth = estimate_bandwidth(X)
bandwidth

1.8158484154517098

4) 군집화 시각화

import pandas as pd
import matplotlib.pyplot as plt

cluster = pd.DataFrame(X,columns=['x0','x1'])
cluster['target'] = y

cluster['meanshift'] = MeanShift(bandwidth = bandwidth).fit_predict(X)

marks = ['o','s','^']
for i in np.unique(cluster.meanshift):
    target = cluster[cluster.meanshift == i]        
    plt.scatter(x=target['x0'], y=target['x1'], marker=marks[i])

5) y(target)값과의 매칭확인

cluster.groupby('target')['meanshift'].value_counts()

3. GMM(Gaussian Mixture Model)

데이터가 여러 개의 가우시안 분포를 가진 집합들로 석여 생성된것이라는 가정하에 군집화 실행
(연속 확률 함수)

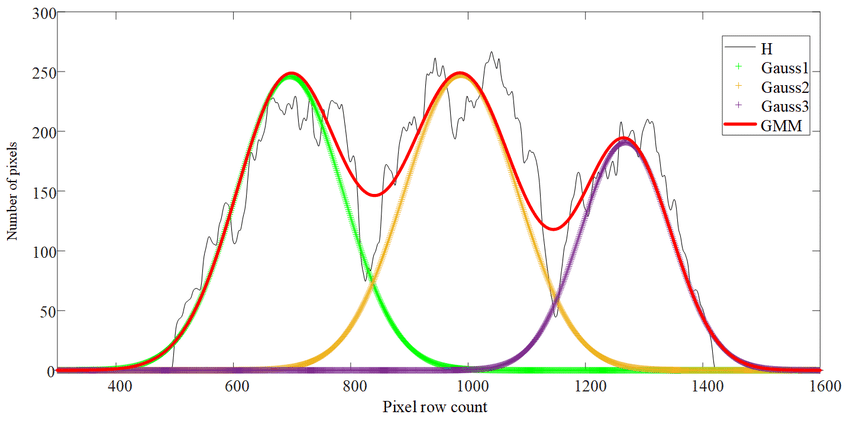
KMeans와의 비교

데이터 세트가 원형의 범위를 가질 수록 KMeans의 군집화 효율이 더 높다
길쭉한 타원형에서는 군집화를 잘 수행하지 못한다.
그림으로 예시를 설명

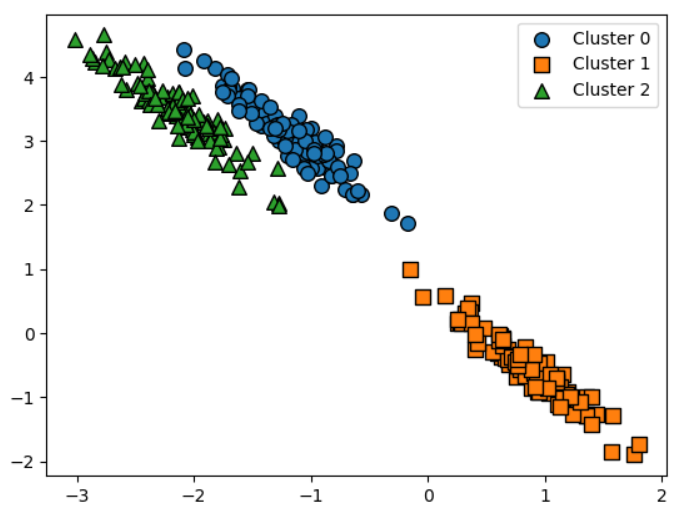
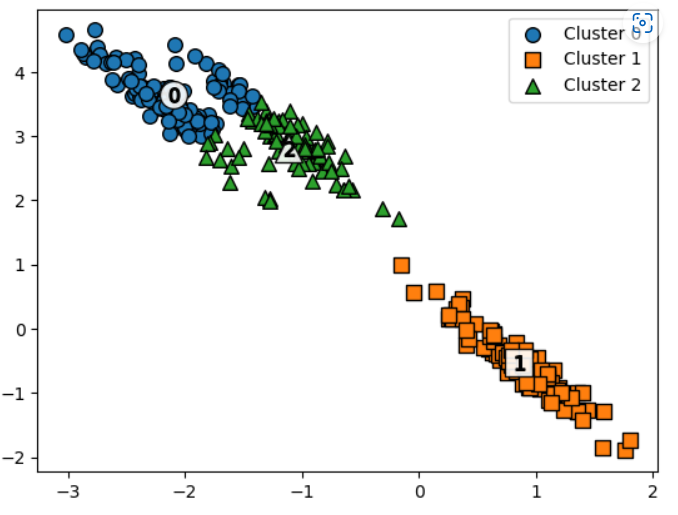
이러한 실제 데이터 세트에서 KMeans를 적용시켜보았을때,

GMM을 적용시켰을때,

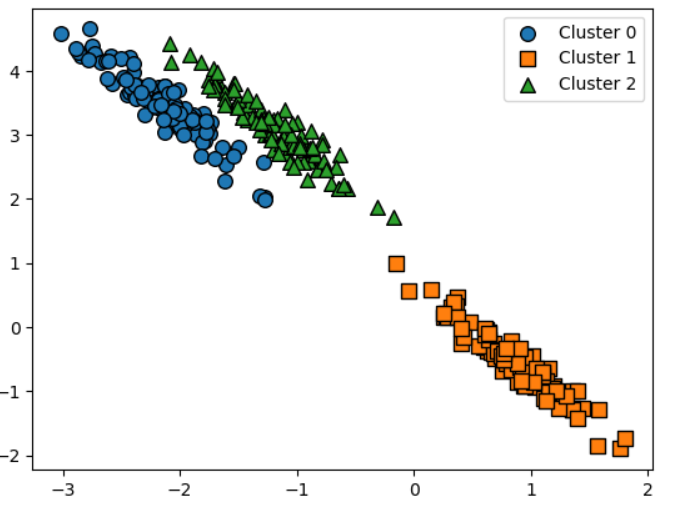
4. DBSCAN

특정공간 내에 데이터 밀도차이를 기반으로한 알고리즘.
데이터의 분포가 기하학적으로 복잡한 데이터 세트에도 효과적인 군집화 가능

DBSCAN 주요 파라미터

eps: 개별데이터를 중심으로 입실론(epsilon)의 반경을 가지는 원형의 영역
- 일반적으로 eps값을 크게하면 주어진 반경에 더 많은 데이터를 포함시키므로 노이즈 데이터 개수가 작아진다.
min_sample: 입실론 주변 영역에 포함되어야 하는 타 데이터의 최소 개수
(min points(타 데이터)+1(자신))
- 일반적으로 min_sample값을 크게하면 주어진 반경 내 더 많은 데이터를 포함시켜야 하므로 노이즈 데이터 개수가 커진다.
- 데이터 밀도가 커져야 하는데, 반경 안에 그만큼 촘촘한 데이터 분포를 갖지 못하는 경우 노이즈로 인식

데이터 포인트 정의

입실론 주변 영역 내 포함되는 최소 데이터 개수를 어떻게 충족하는가

핵심포인트(Core): 주변 영역에 최소 데이터 개수 이상의 타 데이터를 가지고 있는 경우
이웃포인트(Neighbor): 핵심포인트의 주변 영역에 위치한 타 데이터들
경계포인트(Border): 핵심포인트가 되진 못하고, 핵심포인트를 이웃포인트로 가지는 데이터
잡음포인트(Noise): 핵심포인트도 경계포인트도 아닌 데이터

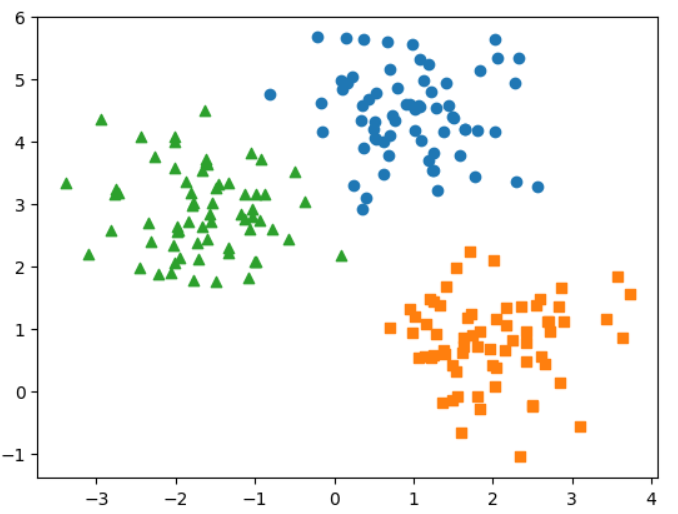
1) 예제 활용: 붓꽃 데이터세트

eps: 0.6

import pandas as pd
import numpy as np

from sklearn.datasets import load_iris

iris = load_iris()
cluster = pd.DataFrame(iris.data, columns = iris.feature_names)

#--------------------------------#
from sklearn.cluster import DBSCAN

dbscan = DBSCAN(eps=.6, min_samples=8, metric='euclidean')
#--------------------------------#
cluster['target'] = iris.target
cluster['dbscan'] = dbscan.fit_predict(iris.data)

cluster.groupby('target')['dbscan'].value_counts()

"-1"이 군집 레이블에 있는 것을 확인할 수 있는데 이는 "노이즈"에 속한다.

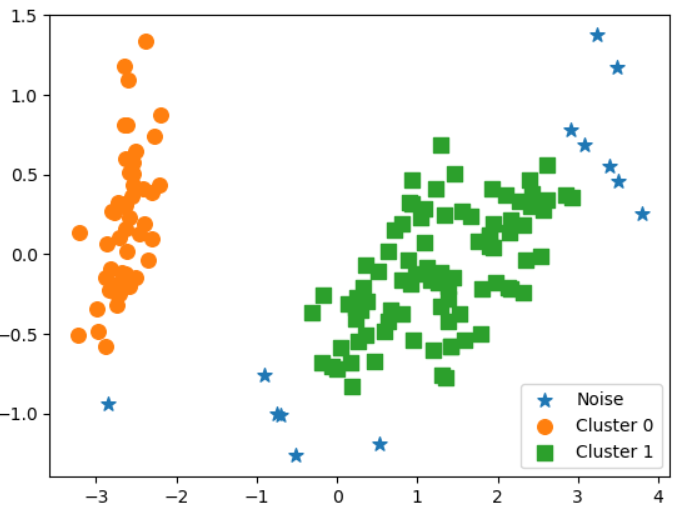
시각화

시각화를 하기위해 2차원으로 차원 축소하기

import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
pca = PCA(n_components=2, random_state=0).fit_transform(iris.data)

cluster['x0'] = pca[:,0]
cluster['x1'] = pca[:,1]

#-----------------------------#
markers=['o', 's', '^', 'x', '*']

for i in np.unique(cluster.dbscan):
    target = cluster[cluster.dbscan==i]
        
    if i == -1: cluster_legend = 'Noise'
    else : cluster_legend = 'Cluster '+str(i)
        
    plt.scatter(x=target['x0'], y=target['x1'], s=70,
                    marker=markers[i], label=cluster_legend)
plt.legend()
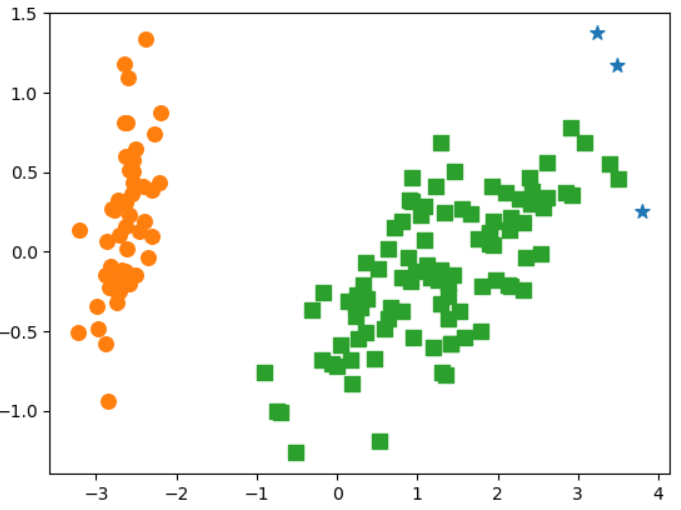
plt.show()

eps: 0.8

iris = load_iris()
df = pd.DataFrame(iris.data, columns = iris.feature_names)

dbscan = DBSCAN(eps=.8, min_samples=8, metric='euclidean')
df['target'] = iris.target
df['dbscan'] = dbscan.fit_predict(iris.data)

df.groupby('target')['dbscan'].value_counts()

시각화

pca = PCA(n_components=2, random_state=0).fit_transform(iris.data)

cluster['x0'] = pca[:,0]
cluster['x1'] = pca[:,1]

markers=['o', 's', '^', 'x', '*']
for i in np.unique(cluster.dbscan):
    target = cluster[cluster.dbscan==i]

    plt.scatter(x=target['x0'], y=target['x1'], s=70, marker=markers[i])

plt.show()

2) 군집화 알고리즘 테스트를 위한 데이터 생성2

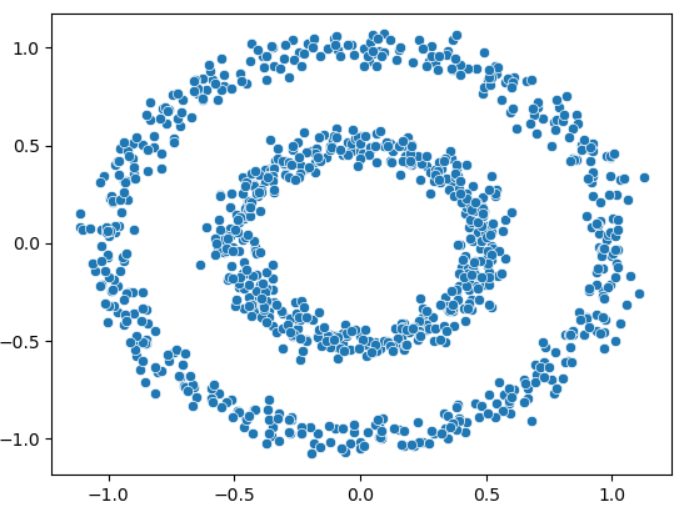
2-1) make_circle()로 데이터 생성

make_circle(): 내부의 원과 외부의 원 형태로 되어있는 2차원 데이터 세트를 만들어 준다.
- 오직 2개의 피처생성
- noise: 데이터 세트의 비율
- factor: 내,외부 원 간 scale비율

from sklearn.datasets import make_circles
import seaborn as sns

X,y = make_circles(n_samples=1000, shuffle=True, noise = 0.05, 
                   random_state=0, factor=.5)
                   
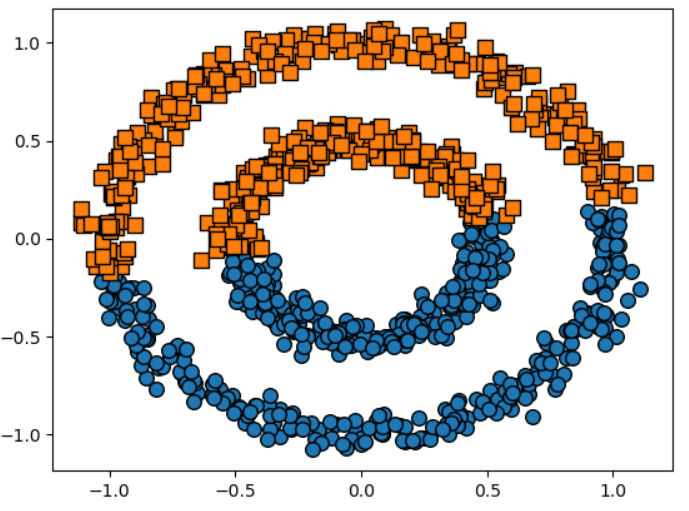
sns.scatterplot(x=X[:,0],y=X[:,1])

DBSCAN적용하기

import pandas as pd
from sklearn.cluster import DBSCAN

dbscan = DBSCAN(eps=.2,min_samples=10,metric='euclidean').fit_predict(X)

#------데이터프레임으로------#
cluster = pd.DataFrame(X, columns = ['x0','x1'])
cluster['target'] = y
cluster['dbscan'] = dbscan

#------시각화------#
markers=['o', 's', '^', 'x', '*']
for i in np.unique(cluster.dbscan):
    target = cluster[cluster.dbscan==i]

    plt.scatter(x=target['x0'], y=target['x1'], s=70, 
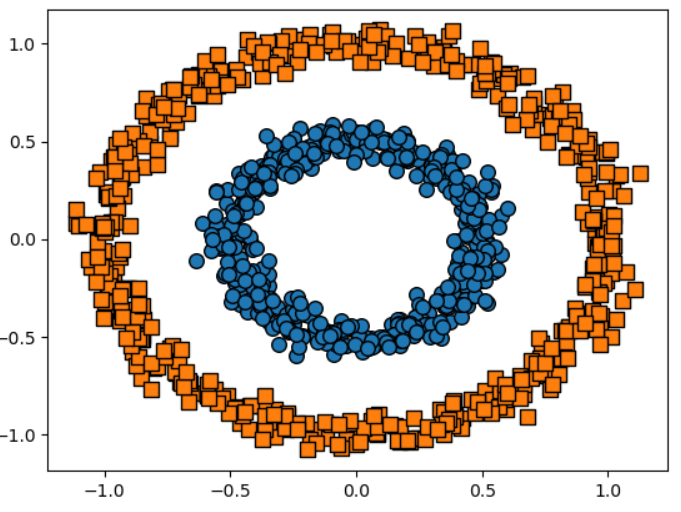
                edgecolor='k', marker=markers[i])

참고: KMeans를 적용한다면?

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters =2, max_iter=1000, random_state=0).fit_predict(X)

#------데이터프레임------#
cluster = pd.DataFrame(X, columns = ['x0','x1'])
cluster['target'] = y
cluster['kmeans'] = kmeans

#------시각화------#
markers=['o', 's', '^', 'x', '*']
for i in np.unique(cluster.kmeans):
    target = cluster[cluster.kmeans==i]

    plt.scatter(x=target['x0'], y=target['x1'], s=70, 
                edgecolor='k', marker=markers[i])