해당 문서는 Coursera 강의 Bayesian Statistics: Techniques and Models 를 보고 공부한 것을 정리한 노트입니다.
1. Components of Bayesian Models
베이지안 모델은 세 가지의 구성물(Likelihood, Prior, Posterior)로 구성된다.
L i k e l i h o o d = P ( y ∣ θ ) Likelihood = P(y|\theta) L i k e l i h o o d = P ( y ∣ θ )
Likelihood는 모수 θ \theta θ
P r i o r = P ( θ ) Prior = P(\theta) P r i o r = P ( θ )
Prior는 사전확률분포라고도 하며, 모수 θ \theta θ
P o s t e r i o r = P ( θ ∣ y ) Posterior = P(\theta|y) P o s t e r i o r = P ( θ ∣ y )
Posterior는 사후확률분포라 하며 data에 의해 조정된 확률분포를 나타낸다.
Posterior는 다음의 식으로 나타내볼 수도 있다. P o s t e r i o r = P ( θ ∣ y ) = P ( θ , y ) P ( y ) Posterior=P(\theta|y)=\frac{P(\theta,y)}{P(y)} P o s t e r i o r = P ( θ ∣ y ) = P ( y ) P ( θ , y ) 조건부 확률 공식으로 위와 같이 사후확률분포를 나타낼 수 있다.
P ( y ) = ∫ P ( θ , y ) d θ P(y)=\int{P(\theta,y)d}\theta P ( y ) = ∫ P ( θ , y ) d θ 이 표현법이 중요한 이유는, 위의 posterior 공식을 다시 써 보면 이해가 된다.
P o s t e r i o r = P ( θ ∣ y ) = P ( θ , y ) P ( y ) = P ( θ , y ) ∫ P ( θ , y ) d θ Posterior=P(\theta|y)=\frac{P(\theta,y)}{P(y)}=\frac{P(\theta,y)}{\int{P(\theta,y)d}\theta} P o s t e r i o r = P ( θ ∣ y ) = P ( y ) P ( θ , y ) = ∫ P ( θ , y ) d θ P ( θ , y ) P ( θ , y ) = P ( y ∣ θ ) P ( θ ) P(\theta,y) = P(y|\theta)P(\theta) P ( θ , y ) = P ( y ∣ θ ) P ( θ ) P o s t e r i o r = P ( θ , y ) ∫ P ( θ , y ) d θ = P ( y ∣ θ ) P ( θ ) ∫ P ( y ∣ θ ) P ( θ ) d θ Posterior=\frac{P(\theta,y)}{\int{P(\theta,y)d}\theta}=\frac{P(y|\theta)P(\theta)}{{\int{P(y|\theta)P(\theta)}d\theta}} P o s t e r i o r = ∫ P ( θ , y ) d θ P ( θ , y ) = ∫ P ( y ∣ θ ) P ( θ ) d θ P ( y ∣ θ ) P ( θ ) 이렇게 표현함으로써 우리는 posterior를 prior와 likelihood의 곱으로 표현할 수 있다는 것을 알게 되었다.
P o s t e r i o r ∝ P r i o r ∗ L i k e l i h o o d Posterior \propto Prior *Likelihood P o s t e r i o r ∝ P r i o r ∗ L i k e l i h o o d 2. Model Specification
다음과 같은 베이지안 모델이 있다고 하자.
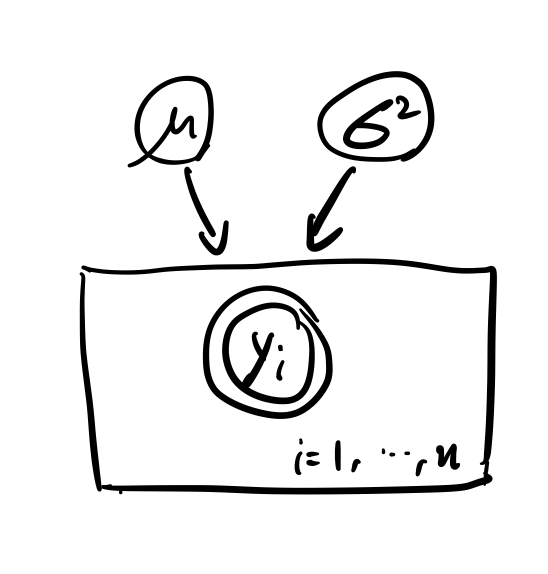
Y i ∣ μ , σ 2 ∼ i i d N ( μ , σ 2 ) , i = 1 , . . . , n Y_i|\mu,\sigma^2 \stackrel{iid}{\sim} N(\mu,\sigma^2), i=1,...,n Y i ∣ μ , σ 2 ∼ i i d N ( μ , σ 2 ) , i = 1 , . . . , n P ( μ , σ 2 ) = P ( μ ) P ( σ 2 ) P(\mu,\sigma^2)=P(\mu)P(\sigma^2) P ( μ , σ 2 ) = P ( μ ) P ( σ 2 ) μ ∼ N ( μ 0 , σ 0 2 ) \mu \sim N(\mu_0,\sigma^2_0) μ ∼ N ( μ 0 , σ 0 2 ) σ 2 ∼ Γ − 1 ( α 0 , β 0 ) \sigma^2 \sim \Gamma^{-1}(\alpha_0,\beta_0) σ 2 ∼ Γ − 1 ( α 0 , β 0 ) 이 모델은 다음과 같이 표현해 볼 수 있다고 한다.
동그라미 하나는 분포의 모수, 그리고 겹동그라미는 관측값을 의미한다. 위에서 복잡했던 수식들이 한눈에 이해된다. 직관적으로 관측값 y i y_i y i μ , σ 2 \mu, \sigma^2 μ , σ 2 Plate라고 하는데, y i y_i y i
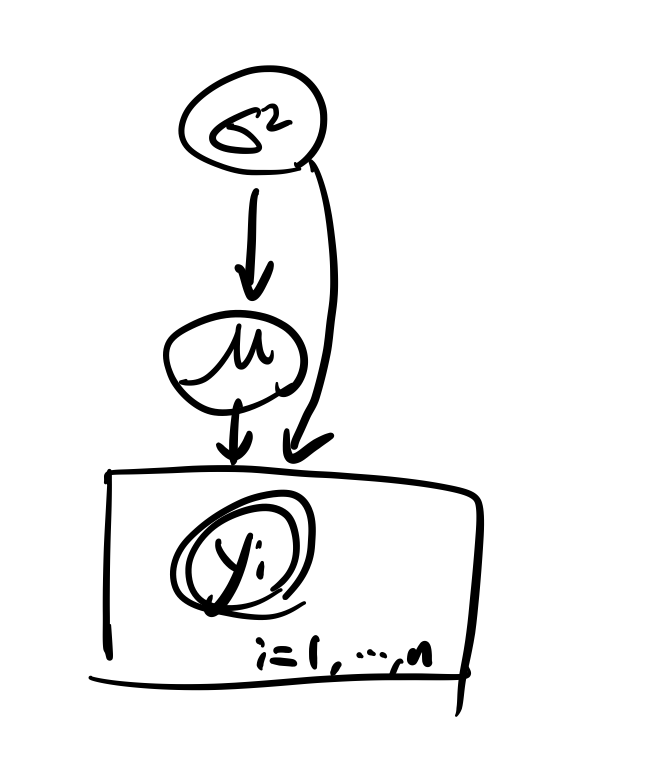
물론 분포가 얽혀 있는 경우에도 이 그림을 사용할 수 있다.
Y i ∣ μ , σ 2 ∼ i i d N ( μ , σ 2 ) , i = 1 , . . . , n Y_i|\mu,\sigma^2 \stackrel{iid}{\sim} N(\mu,\sigma^2), i=1,...,n Y i ∣ μ , σ 2 ∼ i i d N ( μ , σ 2 ) , i = 1 , . . . , n μ ∣ σ 2 ∼ N ( μ 0 , σ 0 2 w 0 ) \mu|\sigma^2 \sim N(\mu_0,\frac{\sigma^2_0}{w_0}) μ ∣ σ 2 ∼ N ( μ 0 , w 0 σ 0 2 ) σ 2 ∼ Γ − 1 ( α 0 , β 0 ) \sigma^2 \sim \Gamma^{-1}(\alpha_0,\beta_0) σ 2 ∼ Γ − 1 ( α 0 , β 0 ) 이렇게 μ \mu μ σ 2 \sigma^2 σ 2
3. Posterior Derivation
위의 베이지안 모델에서,
Y i ∣ μ , σ 2 ∼ i i d N ( μ , σ 2 ) , i = 1 , . . . , n Y_i|\mu,\sigma^2 \stackrel{iid}{\sim} N(\mu,\sigma^2), i=1,...,n Y i ∣ μ , σ 2 ∼ i i d N ( μ , σ 2 ) , i = 1 , . . . , n μ ∣ σ 2 ∼ N ( μ 0 , σ 0 2 w 0 ) \mu|\sigma^2 \sim N(\mu_0,\frac{\sigma^2_0}{w_0}) μ ∣ σ 2 ∼ N ( μ 0 , w 0 σ 0 2 ) σ 2 ∼ Γ − 1 ( α 0 , β 0 ) \sigma^2 \sim \Gamma^{-1}(\alpha_0,\beta_0) σ 2 ∼ Γ − 1 ( α 0 , β 0 ) 관측값과 모수들의 Joint Distribution은 다음과 같이 표현할 수 있다.
P ( y 1 , . . . , y n , μ , σ 2 ) P(y_1,...,y_n,\mu,\sigma^2) P ( y 1 , . . . , y n , μ , σ 2 ) 이것을 Chain rule of probability를 사용하여 펼쳐 보면,
P ( y 1 , . . . , y n , μ , σ 2 ) = P ( y 1 , . . . , y n ∣ μ , σ 2 ) ∗ P ( μ ∣ σ 2 ) ∗ P ( σ 2 ) P(y_1,...,y_n,\mu,\sigma^2)=P(y_1,...,y_n|\mu,\sigma^2)*P(\mu|\sigma^2)*P(\sigma^2) P ( y 1 , . . . , y n , μ , σ 2 ) = P ( y 1 , . . . , y n ∣ μ , σ 2 ) ∗ P ( μ ∣ σ 2 ) ∗ P ( σ 2 ) = ∏ i = 1 n [ N ( y i ∣ μ , σ 2 ) ] ∗ N ( μ ∣ μ 0 , σ 0 2 w 0 ) ∗ Γ − 1 ( σ 2 ∣ α 0 , β 0 ) =\prod_{i=1}^n[N(y_i|\mu,\sigma^2)]*N(\mu|\mu_0,\frac{\sigma^2_0}{w_0})*\Gamma^{-1}(\sigma^2|\alpha_0,\beta_0) = i = 1 ∏ n [ N ( y i ∣ μ , σ 2 ) ] ∗ N ( μ ∣ μ 0 , w 0 σ 0 2 ) ∗ Γ − 1 ( σ 2 ∣ α 0 , β 0 ) 이렇게 된다. 이 식 전체는 베이즈 정리의 분자가 된다. 따라서 관측값과 모수들의 joint distribution은 data에 대한 모수들의 posterior distribution에 proportional 하다.
P ( y 1 , . . . , y n , μ , σ 2 ) ∝ P ( μ , σ 2 ∣ y 1 , . . . , y n ) P(y_1,...,y_n,\mu,\sigma^2) \propto P(\mu,\sigma^2|y_1,...,y_n) P ( y 1 , . . . , y n , μ , σ 2 ) ∝ P ( μ , σ 2 ∣ y 1 , . . . , y n ) 4. Non-Conjugate Models
posterior distribution이 likelihood와 prior의 곱에 proportional 하다는 것은 앞에서 배웠다. 지금까지는 prior distribution과 posterior distribution이 모두 같은 분포일 경우만 보았다. 이것을 conjugate model이라고 한다. 하지만 둘이 서로 다른 모델에서는 어떻게 해야 할까?
다음의 베이지안 모델을 보자.
Y i ∣ μ ∼ i i d N ( μ , 1 ) , i = 1 , . . . , n Y_i|\mu \stackrel{iid}{\sim} N(\mu,1), i=1,...,n Y i ∣ μ ∼ i i d N ( μ , 1 ) , i = 1 , . . . , n μ ∼ t ( 0 , 1 , 1 ) \mu\sim t(0,1,1) μ ∼ t ( 0 , 1 , 1 ) prior과 likelihood를 곱해서 사후 확률 분포를 계산해 보면...P ( μ ∣ y 1 , . . . , y n ) P(\mu|y_1,...,y_n) P ( μ ∣ y 1 , . . . , y n ) ∝ ∏ i = 1 n [ 1 2 π e x p ( − 1 2 ( y i − μ ) 2 ) ] ∗ 1 π ( 1 + μ 2 ) \propto \prod_{i=1}^n[\frac{1}{\sqrt{2\pi}}exp(-\frac{1}{2}(y_i-\mu)^2)]*\frac{1}{\pi(1+\mu^2)} ∝ ∏ i = 1 n [ 2 π 1 e x p ( − 2 1 ( y i − μ ) 2 ) ] ∗ π ( 1 + μ 2 ) 1 ∝ e x p [ − 1 2 ∑ i = 1 n ( y i − μ ) 2 ] ∗ 1 1 + μ 2 \propto exp[-\frac{1}{2}\sum_{i=1}^n(y_i-\mu)^2]*\frac{1}{1+\mu^2} ∝ e x p [ − 2 1 ∑ i = 1 n ( y i − μ ) 2 ] ∗ 1 + μ 2 1 ∝ e x p [ − 1 2 ( ∑ i = 1 n y i 2 − 2 μ ∑ i = 1 n y i + n μ 2 ] ∗ 1 1 + μ 2 \propto exp[-\frac{1}{2}(\sum_{i=1}^ny_i^2-2\mu\sum_{i=1}^ny_i+n\mu^2]*\frac{1}{1+\mu^2} ∝ e x p [ − 2 1 ( ∑ i = 1 n y i 2 − 2 μ ∑ i = 1 n y i + n μ 2 ] ∗ 1 + μ 2 1 ∝ e x p [ n ( y ˉ μ − μ 2 2 ) ] 1 + μ 2 \propto \frac{exp[n(\bar{y}\mu-\frac{\mu^2}{2})]}{1+\mu^2} ∝ 1 + μ 2 e x p [ n ( y ˉ μ − 2 μ 2 ) ]
매우 어글리한 사후확률분포가 나왔다. 이 분포는 컴퓨터 없이는 적분하기도 어려울 뿐더러 지금까지 배운 베이즈 통계의 hierarchical 모델을 사용할 수 없다.
내용에 대한 질문, 잘못된 부분에 대한 지적 모두 환영합니다!