[구현] BOJ_14719 빗물 "JAVA"

🚀링크

https://www.acmicpc.net/problem/14719

💻문제

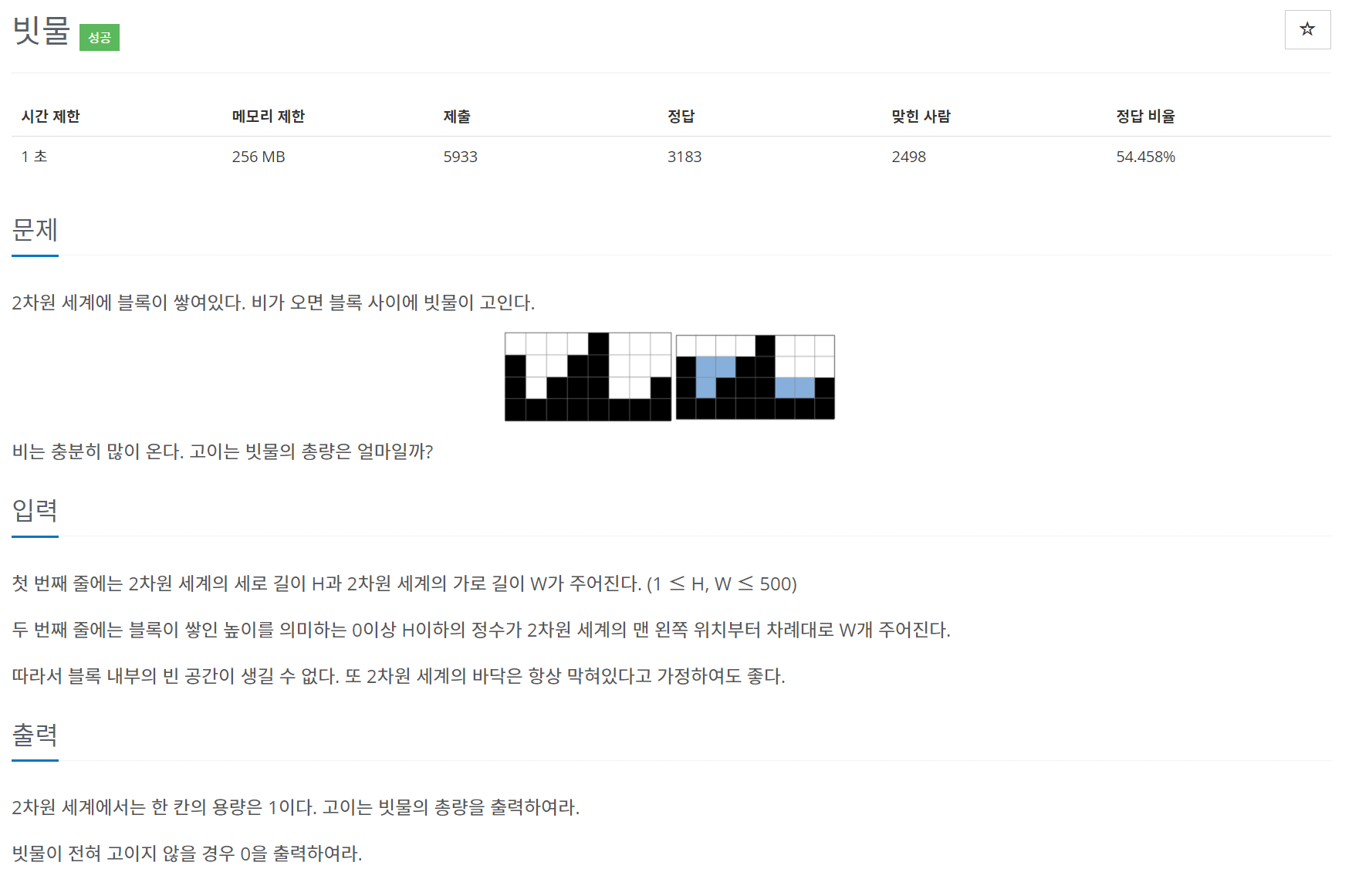
🌏문제풀이

처음엔 2차원배열로 구현하여 값을 구하려 했지만, 1부터 W-1까지 단건의 값을 구하여 더하는 것이 더욱 효율적이라 아래와 같은 방법으로 풀었다.

맨 오른쪽과 왼쪽은 빗물이 쌓일 수 없는 구조기 때문에 1~W-1까지를 기준으로 잡았다.

i를 기준으로 for(int j=0; j<i; j++), for(int t=i+1; t<W; t++)를 순환하며 각각의 max값을 구하고, 이 둘 중 min값을 찾는다.
이는 앙 옆으로 가장 높은 값들 중 작은값을 기준으로 빗물이 쌓일 수 있기 때문이다.

최종적으로 찾은 빗물이 쌓이는 높이에 자기 자신의 높이값을 빼주면 단 건별 빗물이 쌓이는 높이를 구할 수 있다.

👩‍💻코드

package javaTest;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class BOJ_14719_빗물 {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = null;
		
		st = new StringTokenizer(br.readLine());
		int N = Integer.parseInt(st.nextToken());
		int M = Integer.parseInt(st.nextToken());
		
		int block[] = new int[M];
		int sum = 0;
		
		st = new StringTokenizer(br.readLine());
		for(int i=0; i<M; i++) {
			block[i] = Integer.parseInt(st.nextToken());
			
		}
		
		//맨 오른쪽과 왼쪽은 벽으로 생각해야하기 때문에 반복문에서 제외
		for(int i=1; i<M-1; i++) {
			int left = 0;
			int right = 0;
			
			//기준점으로부터 왼쪽 기둥 중 가장 큰 값
			for(int j=0; j<i; j++) {
				left = Math.max(left, block[j]);
			}
			//기준점으로부터 오른쪽 기둥 중 가장 큰 값
			for(int t=i+1; t<M; t++) {
				right = Math.max(right, block[t]);
			}
			//왼쪽,오른쪽 가장 큰 값이 자기자신보다 작으면 빗물을 담지 못함으로 if처리로 거름
			if(left > block[i] && right > block[i]) {
				//왼쪽, 오른쪽 기둥 중 더 작은 기둥 높이 기준 - 자신의 높이
				sum += Math.min(left, right) - block[i];
			}
		}
		
		System.out.print(sum);
		

	}
	

}