99클럽 코테 스터디 4기 9일차 TIL - 백준: 나이트의 이동(7562) Swift & Python

레일리·2024년 11월 5일

99클럽 코테 스터디 4기

목록 보기

9/26

ℹ️ 문제 정보

플랫폼	번호	제목	유형	난이도	언어
백준	7562	나이트의 이동	BFS	실버1	Swift, Python

🚀 나의 접근 방법

이 문제는 나이트가 최소 몇 번 만에 이동할 수 있는지(최단거리)를 구하는 것이기 때문에 BFS를 이용하면 된다.

물론 DFS로도 해결할 수 있지만 탐색할 때 마다 항상 비교하며 최소 거리를 갱신해 줘야 해서 비효율 적이다. (보통 최단거리는 BFS를 사용한다)

BFS를 사용하기로 결정했으면 나이트가 이동할 방향을 정의해야 한다.

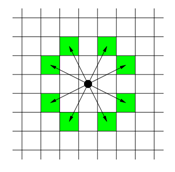
나이트는 위와 같이 움직일 수 있다. 그러면 8가지의 이동을 아래와 같이 정의할 수 있다.

let dx = [-2, -1, 1, 2,  2,  1, -1, -2]
let dy = [ 1,  2, 2, 1, -1, -2, -2, -1]

위 방향 배열을 아래와 같이 for 문으로 접근하여 사용하면 된다.

for i in 0..<8 {
	let nx = x + dx[i]
	let ny = y + dy[i]
}

이를 활용해 BFS를 사용하여 원하는 좌표를 찾으면 이동한 거리를 출력하면 된다.

✍️ 나의 코드

Swift

let T = Int(readLine()!)!

for _ in 0..<T {
    let length = Int(readLine()!)!
    let start = readLine()!.split(separator: " ").map{ Int($0)! }
    let (startX, startY) = (start[0], start[1])
    let end = readLine()!.split(separator: " ").map{ Int($0)! }
    let (endX, endY) = (end[0], end[1])
    
    var graph = Array(repeating: Array(repeating: false, count: length), count: length)
    
    let dx = [-2, -1, 1, 2,  2,  1, -1, -2]
    let dy = [ 1,  2, 2, 1, -1, -2, -2, -1]
    
    func bfs(_ x: Int, _ y: Int) {
        var queue = [(x, y, 0)]
        var idx = 0
        graph[x][y] = true
        
        while queue.count > idx {
            let n = queue[idx]
            let x = n.0
            let y = n.1
            let count = n.2
            
            if x == endX && y == endY {
                print(count)
                break
            }
            
            for i in 0..<8 {
                let nx = x + dx[i]
                let ny = y + dy[i]
                
                if nx < 0 || nx > (length - 1) || ny < 0 || ny > (length - 1) {
                    continue
                }
                
                if !graph[nx][ny] {
                    graph[nx][ny] = true
                    queue.append((nx, ny, count+1))
                }
            }
            idx += 1
        }
    }
    bfs(startX, startY)
}

Python

from collections import deque

T = int(input())

for _ in range(T):
    length = int(input())
    startX, startY = map(int, input().split(" "))
    endX, endY = map(int, input().split(" "))

    graph = [[False] * length for i in range(length)]

    dx = [-2, -1, 1, 2,  2,  1, -1, -2]
    dy = [ 1,  2, 2, 1, -1, -2, -2, -1]

    def bfs(x, y):
        queue = deque([(x, y, 0)])
        graph[x][y] = True

        while len(queue) > 0:
            n = queue.popleft()
            x, y, count = n[0], n[1], n[2]

            if x == endX and y == endY:
                print(count)
                break

            for i in range(8):
                nx = x + dx[i]
                ny = y + dy[i]

                if nx < 0 or nx > length - 1 or ny < 0 or ny > length - 1:
                    continue
                
                if not graph[nx][ny]:
                    queue.append((nx, ny, count + 1))
                    graph[nx][ny] = True

    bfs(startX, startY)