벡터와 행렬 연산

소프트맥스 회귀에서는 종속 변수 y의 종류도 3개 이상이 되면서 더욱 복잡해집니다. 그리고 이러한 식들이 겹겹이 누적되면 인공 신경망의 개념이 됩니다.

케라스는 사용하기가 편리해서 이런 고민을 할 일이 상대적으로 적지만, Numpy나 텐서플로우의 로우-레벨(low-level)의 머신 러닝 개발을 하게되면 각 변수들의 연산을 벡터와 행렬 연산으로 이해할 수 있어야 합니다. 다시 말해 사용자가 데이터와 변수의 개수로부터 행렬의 크기, 더 나아 텐서의 크기를 산정할 수 있어야 합니다. 이번 챕터에서는 기본적인 벡터와 행렬 연산에 대해서 이해해보겠습니다.

벡터와 행렬과 텐서

벡터는 크기와 방향을 가진 양입니다. 숫자가 나열된 형상이며 파이썬에서는 1차원 배열 또는 리스트로 표현합니다. 반면, 행렬은 행과 열을 가지는 2차원 형상을 가진 구조입니다. 파이썬에서는 2차원 배열로 표현합니다. 가로줄을 행(row)라고 하며, 세로줄을 열(column)이라고 합니다. 3차원부터는 주로 텐서라고 부릅니다. 텐서는 파이썬에서는 3차원 이상의 배열로 표현합니다.

텐서(tensor)

인공 신경망은 복잡한 모델 내의 연산을 주로 행렬 연산을 통해 해결합니다. 그런데 여기서 말하는 행렬 연산이란 단순히 2차원 배열을 통한 행렬 연산만을 의미하는 것이 아닙니다. 머신 러닝의 입, 출력이 복잡해지면 3차원 텐서에 대한 이해가 필수로 요구됩니다. 예를 들어 인공 신경망 모델 중 하나인 RNN에서는 3차원 텐서에 대한 개념을 모르면 RNN을 이해하기가 쉽지 않습니다.

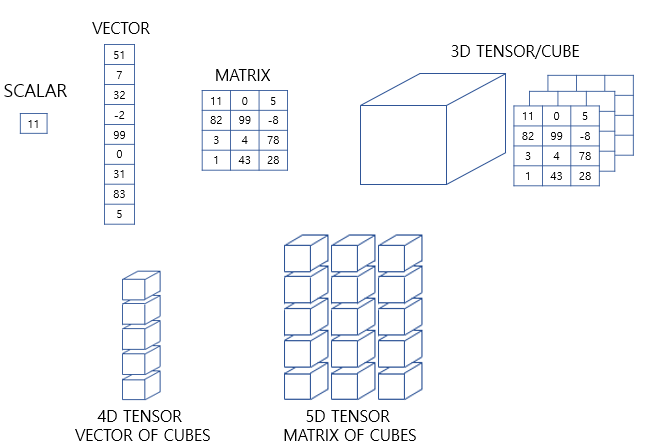
1) 0차원 텐서

스칼라는 하나의 실수값으로 이루어진 데이터를 말합니다. 또한 스칼라값을 0차원 텐서라고 합니다. 차원을 영어로 Dimensionality라고 하므로 0D 텐서라고도 합니다.

import numpy as np
d=np.array(5)
print(d.ndim)
print(d.shape)

결과

0
()

2) 1차원 텐서

숫자를 특정 순서대로 배열한 것을 벡터라고합니다. 또한 벡터를 1차원 텐서라고 합니다. 주의할 점은 벡터의 차원과 텐서의 차원은 다른 개념이라는 점입니다. 아래의 예제는 4차원 벡터이지만, 1차원 텐서입니다. 1D 텐서라고도 합니다.

d=np.array([1,2,3,4])
print(d.ndim)
print(d.shape)

결과

1
(4,)

벡터의 차원과 텐서의 차원의 정의로 인해 혼동할 수 있는데 벡터에서의 차원(Dimensionality)은 하나의 축에 차원들이 존재하는 것이고, 텐서에서의 차원(Dimensionality)은 축의 개수를 의미합니다.

3) 2차원 텐서

행과 열이 존재하는 벡터의 배열. 즉, 행렬(matrix)을 2차원 텐서라고 합니다. 2D 텐서라고도 합니다.

d=np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print(d.ndim)
print(d.shape)

결과

2
(3, 4)

텐서의 크기를 보고 머리 속에 떠올릴 수 있으면 모델 설계 시에 유용합니다. 이게 어렵다면, 큰 단위부터 확장해나가며 생각하면 됩니다. 위의 경우 3개의 커다란 데이터가 있는데, 그 각각의 커다란 데이터는 작은 데이터 4개로 이루어졌다고 생각할 수 있습니다.

1차원 텐서를 벡터, 2차원 텐서를 행렬로 비유하였는데 수학적으로 행렬의 열을 열벡터로 부르거나, 열벡터를 열행렬로 부르는 것과 혼동해서는 안 됩니다. 여기서 말하는 1차원 텐서와 2차원 텐서는 차원 자체가 달라야 합니다.

4)3차원 텐서

행렬 또는 2차원 텐서를 단위로 한 번 더 배열하면 3차원 텐서라고 부릅니다. 3D 텐서라고도 합니다. 사실 위에서 언급한 0차원 ~ 2차원 텐서는 각각 스칼라, 벡터, 행렬이라고 해도 무방하므로 3차원 이상의 텐서부터 본격적으로 텐서라고 부릅니다. 조금 쉽게 말하면 데이터 사이언스 분야 한정으로 주로 3차원 이상의 배열을 텐서라고 부릅니다. (엄밀한 수학적 정의로는 아닙니다.) 그렇다면 3D 텐서는 적어도 여기서는 3차원 배열로 이해하면 되겠습니다.

이 3차원 텐서의 구조를 이해하지 않으면, 복잡한 인공 신경망의 입, 출력값을 이해하는 것이 쉽지 않습니다. 개념 자체는 어렵지 않지만 반드시 알아야하는 개념입니다.

d=np.array([
            [[1, 2, 3, 4, 5], [6, 7, 8, 9, 10], [10, 11, 12, 13, 14]],
            [[15, 16, 17, 18, 19], [19, 20, 21, 22, 23], [23, 24, 25, 26, 27]]
            ])
print(d.ndim)
print(d.shape)

결과

3
(2, 3, 5)

2개의 큰 데이터가 있는데, 그 각각은 3개의 더 작은 데이터로 구성되며, 그 3개의 데이터는 또한 더 작은 5개의 데이터로 구성되어져 있습니다.

자연어 처리에서 특히 자주 보게 되는 것이 이 3D 텐서입니다. 3D 텐서는 시퀀스 데이터(sequence data)를 표현할 때 자주 사용되기 때문입니다. 여기서 시퀀스 데이터는 주로 단어의 시퀀스를 의미하며, 시퀀스는 주로 문장이나 문서, 뉴스 기사 등의 텍스트가 될 수 있습니다. 이 경우 3D 텐서는 (samples, timesteps, word_dim)이 됩니다. 또는 일괄로 처리하기 위해 데이터를 묶는 단위인 배치의 개념에 대해서 뒤에서 배울텐데 (batch_size, timesteps, word_dim)이라고도 볼 수 있습니다.

samples/batch_size는 데이터의 개수, timesteps는 시퀀스의 길이, word_dim은 단어를 표현하는 벡터의 차원을 의미합니다. 더 상세한 설명은 RNN 챕터에서 배우게 되겠지만 자연어 처리에서 왜 3D 텐서의 개념이 사용되는지 간단한 예를 들어봅시다. 다음과 같은 훈련 데이터가 있다고 해봅시다.

• 문서1 : I like NLP
• 문서2 : I like DL
• 문서3 : DL is AI

이를 인공 신경망의 모델의 입력으로 사용하기 위해서는 각 단어를 벡터화해야 합니다. 단어를 벡터화하는 방법으로는 원-핫 인코딩이나 워드 임베딩이라는 방법이 대표적이나 워드 임베딩은 아직 배우지 않았으므로 원-핫 인코딩으로 모든 단어를 벡터화 해보겠습니다.

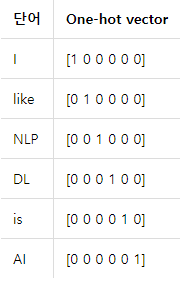
그럼 기존에 있던 훈련 데이터를 모두 원-핫 벡터로 바꿔서 인공 신경망의 입력으로 한 꺼번에 사용한다고 하면 다음과 같습니다. (이렇게 훈련 데이터를 여러개 묶어서 한 꺼번에 입력으로 사용하는 것을 배치(Batch)라고 합니다.)

[[[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0]],
[[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0]],
[[0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 0, 1]]]

이는 (3, 3, 6)의 크기를 가지는 3D 텐서입니다.

5)그 이상의 텐서

3차원 텐서를 배열로 합치면 4차원 텐서가 됩니다. 4차원 텐서를 배열로 합치면 5차원 텐서가 됩니다. 이런 식으로 텐서는 배열로서 계속해서 확장될 수 있습니다.

벡터와 행렬의 연산

1)벡터와 행렬의 덧셈과 뺄셈

같은 크기의 두 개의 벡터나 행렬은 덧셈과 뺄셈을 할 수 있습니다. 이 경우 같은 위치의 원소끼리 연산하면 됩니다. 이러한 연산을 요소별(element-wise) 연산이라고 합니다. 다음과 같이 a와 b라는 두 개의 벡터가 있다고 해봅시다.

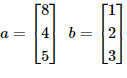
이 때 두 벡터 a와 b의 덧셈과 뺄셈은 아래와 같습니다.

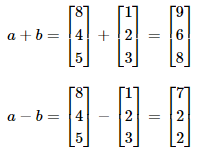
a = np.array([8, 4, 5])
b = np.array([1, 2, 3])
print(a+b)
print(a-b)

결과

[9 6 8]
[7 2 2]

행렬도 마찬가지입니다. 다음과 같이 a와 b라는 두 개의 행렬이 있다고 하였을 때, 두 행렬 a와 b의 덧셈과 뺄셈은 아래와 같습니다.

import numpy as np
a = np.array([[10, 20, 30, 40], [50, 60, 70, 80]])
b = np.array([[5, 6, 7, 8],[1, 2, 3, 4]])
print(a+b)
print(a-b)

결과

[[15 26 37 48]
 [51 62 73 84]]
[[ 5 14 23 32]
 [49 58 67 76]]

2)벡터의 내적과 행렬의 곱셈

벡터의 점곱(dot product) 또는 내적(inner product)에 대해 알아봅시다. 벡터의 내적은 연산을 점(dot)으로 표현하기도 합니다.

내적이 성립하기 위해서는 두 벡터의 차원이 같아야 하며, 두 벡터 중 앞의 벡터가 행벡터(가로 방향 벡터)이고 뒤의 벡터가 열벡터(세로 방향 벡터)여야 합니다. 아래는 두 벡터의 차원이 같고 곱셈의 대상이 각각 행벡터이고 열벡터일 때 내적이 이루어지는 모습을 보여줍니다. 벡터의 내적의 결과는 스칼라가 된다는 특징이 있습니다.

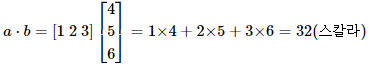
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
print(np.dot(a,b))

결과

32

행렬의 곱셈을 이해하기 위해서는 벡터의 내적을 이해해야 합니다. 행렬의 곱셈은 왼쪽 행렬의 행벡터(가로 방향 벡터)와 오른쪽 행렬의 열벡터(세로 방향 벡터)의 내적(대응하는 원소들의 곱의 합)이 결과 행렬의 원소가 되는 것으로 이루어집니다. 다음과 같이 a와 b라는 두 개의 행렬이 있다고 하였을 때, 두 행렬 a와 b의 곱셈은 아래와 같습니다.

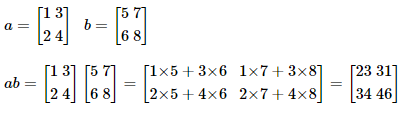
a = np.array([[1, 3],[2, 4]])
b = np.array([[5, 7],[6, 8]])
print(np.matmul(a,b))

결과

[[23 31]
 [34 46]]

다중 선형 회귀 행렬 연산으로 이해하기

독립 변수가 2개 이상일 때, 1개의 종속 변수를 예측하는 문제를 행렬의 연산으로 표현한다면 어떻게 될까요? 다중 선형 회귀나 다중 로지스틱 회귀가 이러한 연산의 예인데, 여기서는 다중 선형 회귀를 통해 예를 들어보겠습니다. 다음은 독립 변수 x가 n개인 다음과 같은 다중 선형 회귀 수식입니다.

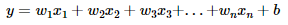
이는 입력 벡터 x와 가중치 벡터 w의 내적으로 표현할 수 있습니다.

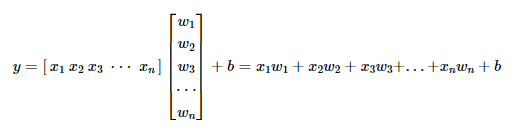
또는 가중치 벡터 w와 입력 벡터 x의 내적으로 표현할 수도 있습니다.

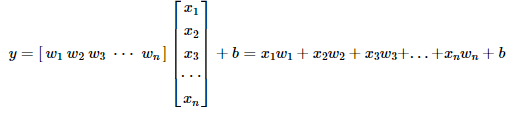
그런데 데이터의 개수가 많을 경우에는 벡터의 내적이 아니라 행렬의 곱셈으로 표현이 가능합니다. 다중 선형 회귀에서 데이터의 개수가 여러개일 때, 행렬의 곱셈으로 어떻게 표현할 수 있는지 예를 들어봅시다. 다음은 집의 크기, 방의 수, 층의 수, 집이 얼마나 오래되었는지와 집의 가격이 기록된 부동산 데이터라고 가정합시다. 해당 데이터를 학습하여 새로운 집의 정보가 들어왔을 때, 집의 가격을 예측해본다고 합시다.

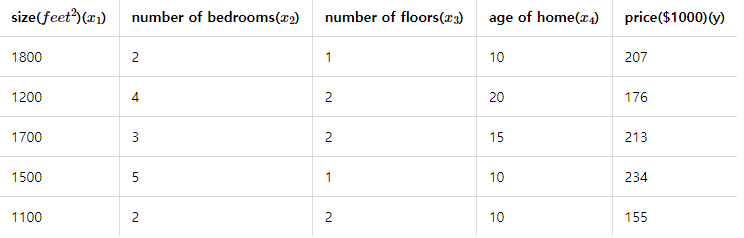
위의 데이터에 대해서 입력 행렬 X와 가중치 벡터 W의 곱으로 표현하면 다음과 같습니다.

여기에 편향 벡터 B를 더 해주면 위 데이터에 대한 전체 가설 수식 H(X)를 표현할 수 있습니다.

위의 수식에서 입력 행렬 X는 5행 4열의 크기를 가집니다. 출력 벡터를 Y라고 하였을 때 Y는 5행 1열의 크기를 가집니다. 여기서 곱셈이 성립하기 위해서 가중치 벡터 W의 크기는 4행 1열을 가져야함을 추론할 수 있습니다.

만약 가중치 벡터를 앞에 두고 입력 행렬을 뒤에 두고 행렬 연산을 한다면 이는 아래와 같습니다.

이는 연산 방법의 차이일뿐 어떤 것이 맞다고, 틀리다고 할 수는 없습니다. 다만, 수학적 관례로 아래와 같이 수식으로 표현할 때는 주로 가중치 W가 입력 X의 앞에 오므로 위 두 가지 경우를 모두 염두하는 것이 좋습니다.

H(X) = WX+B

인공 신경망도 본질적으로 위와 같이 훈련 데이터에 대한 행렬 연산이므로 이번 예제는 반드시 이해해야 합니다.

샘플(Sample)과 특성(Feature)

훈련 데이터의 입력 행렬을 X라고 하였을 때 샘플(Sample)과 특성(Feature)의 정의는 다음과 같습니다.

머신 러닝에서는 데이터를 셀 수 있는 단위로 구분할 때, 각각을 샘플이라고 부르며, 종속 변수 y를 예측하기 위한 각각의 독립 변수 x를 특성이라고 부릅니다.

가중치와 편향 행렬의 크기 결정

여기서는 특성을 행렬의 열로 보는 경우를 가정하여 행렬의 크기가 어떻게 결정되는지 정리합니다.

행렬곱은 두 가지 정의를 가지는데, 두 개의 행렬 J와 K의 곱은 다음과 같은 조건을 충족해야 합니다.
1) 두 행렬의 곱 J x K에 대하여 행렬 J의 열의 수와 행렬 K의 행의 수는 같아야 한다.
2) 두 행렬의 곱 J x K의 결과로 나온 행렬 JK의 크기는 J의 행의 크기와 K의 열의 크기를 가진다.

이로부터 주어진 데이터가 입력과 출력의 행렬의 크기를 어떻게 가지느냐에 따라서 가중치 W의 행렬과 편향 b의 행렬의 크기를 찾아낼 수 있습니다. 독립 변수 x의 행렬을 X, 종속 변수 y의 행렬을 Y라고 하였을 때, 가중치 W의 행렬을 W, 편향 b의 행렬을 B라고 해봅시다. 이때 행렬 X는 또한 입력 행렬(Input Matrix)이라고 부를 수 있고, Y는 출력 행렬(Output Matrix)이라고 부를 수 있습니다.

이제 입력 행렬의 크기와 출력 행렬의 크기로부터 W행렬과 B행렬의 크기를 추론해봅시다.

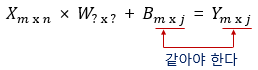
우선 행렬의 덧셈에 해당되는 B행렬은 Y행렬의 크기에 영향을 주지 않습니다. 그러므로 B행렬의 크기는 Y행렬의 크기와 같습니다.

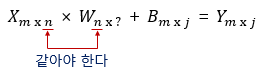
행렬의 곱셈이 성립되려면 행렬의 곱셈에서 앞에 있는 행렬의 열의 크기와 뒤에 있는 행렬의 행의 크기는 같아야 합니다. 그러므로 입력 행렬 X로부터 W행렬의 행의 크기가 결정됩니다.

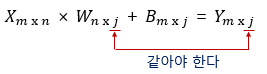
두 행렬의 곱의 결과로서 나온 행렬의 열의 크기는 행렬의 곱에서 뒤에 있는 행렬의 열의 크기와 동일합니다. 그러므로 출력 행렬 Y로부터 W행렬의 열의 크기가 결정됩니다. 인공 신경망 챕터에서 다시 언급하게 되겠지만 배치에 대한 개념을 미리 정리하고 가겠습니다. 이 때 위의 식에서 X행렬의 행을 의미하는 수치 m은 샘플 데이터를 몇 개씩 묶어서 처리하느냐에 따라 달라집니다. 전체 샘플 데이터에 대해서 한 꺼번에 행렬 연산을 하고자한다면, m은 전체 샘플의 개수가 됩니다. 위에서 본 다중 선형 회귀에서 5개의 전체 샘플을 가지고 세웠던 행렬 연산식이 그러한 예입니다.

하지만 전체 샘플 데이터 중 1개씩 불러와서 처리하고자한다면 m은 1이 됩니다. 또는 전체 데이터를 임의의 m개씩 묶인 작은 그룹들로 분할하여 여러번 처리할 수도 있는데 이렇게 처리하면서 기계가 학습하는 것을 미니배치 학습이라고 합니다. 예를 들어 전체 데이터가 1,024개가 있을 때 m을 64로 잡는다면 전체 데이터는 16개의 그룹으로 분할됩니다. 각 그룹은 총 64개의 샘플로 구성됩니다. 그리고 위에서 설명한 행렬 연산을 총 16번 반복하게되고 그제서야 전체 데이터에 대한 학습이 완료됩니다. 이때 64를 배치 크기(Batch size)라고 합니다.