엔트로피(Entropy)와 크로스 엔트로피(Cross-Entropy)

Entropy

엔트로피는 불확실성의 척도로 정보이론에서의 엔트로피는 불확실성을 나타내며 엔트로피가 높다는 것은 정보가 많고 확률이 낮다는 것을 의미합니다

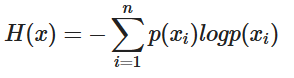
이런 설명과 수식으로는 처음에는 와닿지가 않습니다. 제가 이해한 불확실성이라는 것은 어떤 데이터가 나올지 예측하기 어려운 경우라고 받아들이는 것이 더 직관적입니다.

1.1 예시 : 동전 던지기 & 주사위 던지기

• 동전을 던졌을 때, 앞/뒷면이 나올 확률을 모두 1/2라고 하겠습니다.
• 주사위를 던졌을 때, 각 6면이 나올 확률을 모두 1/6이라고 하겠습니다.
  위의 두 상황에서 불확실성(어떤 데이터가 나올지 예측하기 어려운 것)은 주사위가 더 크다고 직관적으로 다가옵니다. 이를 수식적으로 계산하면 각각 아래와 같습니다.
  
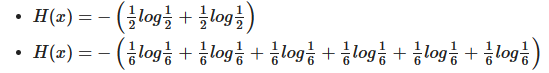
  동전의 엔트로피 값은 약 0.693, 주사위의 엔트로피 값은 1.79 정도로 주사위의 엔트로피 값이 더 높다는 것을 알 수 있습니다. 즉, 무엇이 나올지 알기 어려운 주사위의 경우가 엔트로피가 더 높은 것이죠.

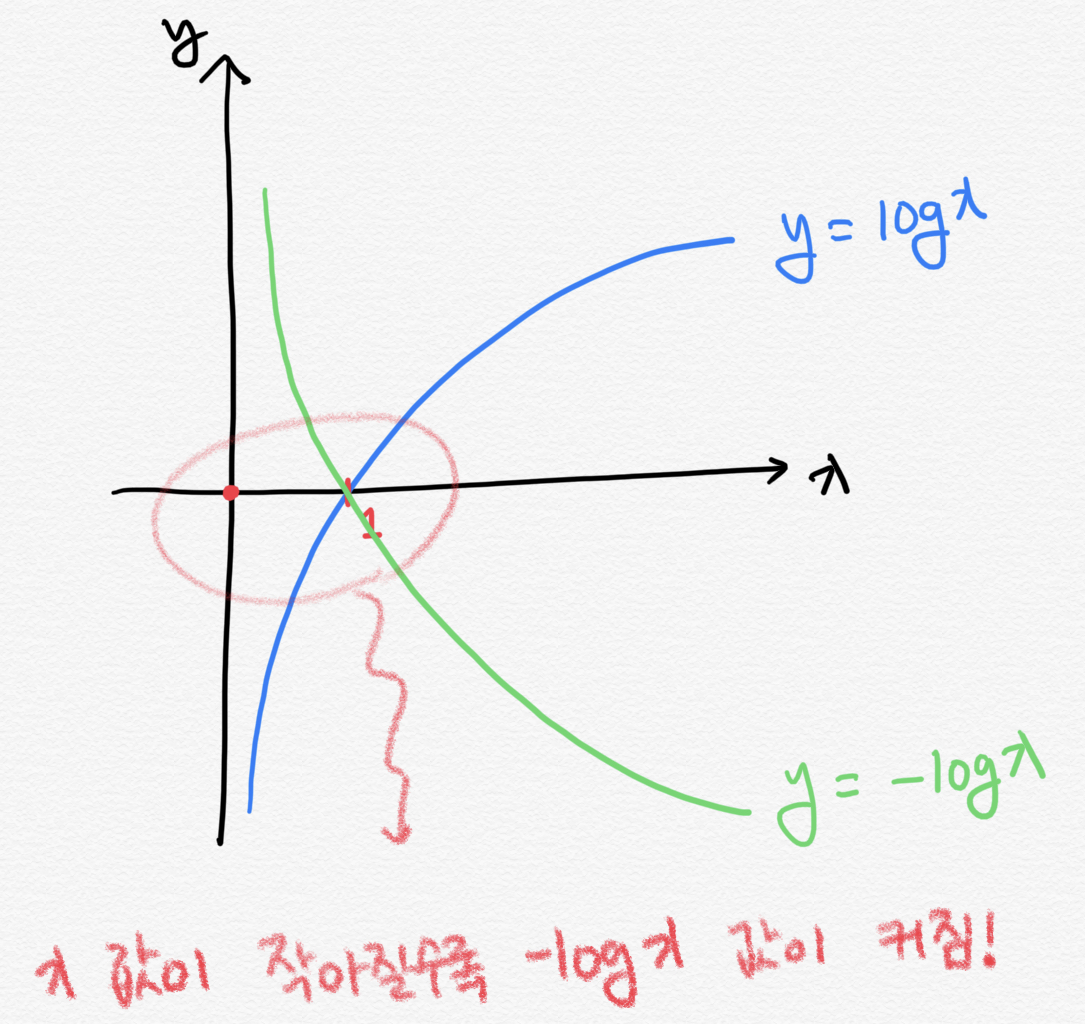
이를 위의 그래프를 통해 살펴보면 이렇게 해석할 수 있습니다.

위의 수식을 아래의 수식으로 바꿔봅니다.

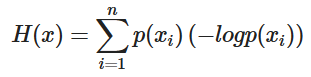
p(xi)는 각각의 요소들이 나올 수 있는 확률값입니다. 모든 요소들이 나올 확률이 동일하다면, -log p(xi) 값도 모두 동일하기 때문에 식을 간결하게 만들 수 있습니다

p(xi)값의 총 합은 1이기 때문에 수식은 -log p(xi)가 됩니다. x값이 작아질수록 -log x 값은 기하급수적으로 커집니다. x가 작아진 것 보다 log x가 커지는 폭이 훨씬 크기 때문에 전체 엔트로피는 증가합니다

1.2 예시 : 공 꺼내기

다른 예시를 통해서 이해를 좀 더 돕겠습니다.

• 전체 공이 100개이다. 공 하나만 빨간색이고, 나머지는 모두 검은색이다.
• 전체 공이 100개이다. 공 50개는 빨간색이고, 나머지는 모두 검은색이다.

위의 경우에는 직관적으로 첫 번째 사례에서 검은 색이 나올 확률이 높으니 불확실성이 적겠군 이라고 생각할 수 있습니다. 실제로 엔트로피를 계산하면 후자가 훨씬 크게 나옵니다.

Cross-Entropy

원래의 cross entropy는 예측 모형은 실제 분포인 q 를 모르고, 모델링을 하여 q 분포를 예측하고자 하는 것이다. 예측 모델링을 통해 구한 분포를 p(x) 라고 해보자. 실제 분포인 q를 예측하는 p 분포를 만들었을 때, 이 때 cross-entropy 는 아래와 같이 정의된다.

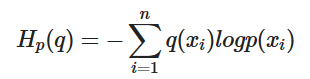
크로스 엔트로피는두 확률 분포의 차이를 구하기 위해서 사용된다. 딥러닝에서는 실제 데이터의 확률 분포와, 학습된 모델이 계산한 확률 분포의 차이를 구하는데 사용된다. q와 p가 모두 들어가서 크로스 엔트로피라고 합니다.

머신러닝을 통한 예측 모형에서 훈련 데이터에서는 실제 분포인 q 를 알 수 있기 때문에 cross-entropy 를 계산할 수 있다. 즉, 훈련 데이터를 사용한 예측 모형에서 cross-entropy 는 실제 값과 예측값의 차이 (dissimilarity) 를 계산하는데 사용할 수 있다는 것이다.

예를 들어, 가방에 0.8/0.1/0.1 의 비율로, 빨간/녹색/노랑 공이 들어가 있다고 하자, 하지만 직감에는 0.2/0.2/0.6의 비율로 들어가 있을 것 같다. 이 때, entropy 와 cross-entropy 는 아래와 같이 계산된다.

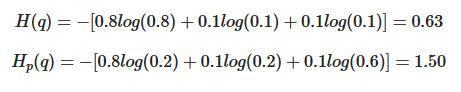
Kullback-Leibler Divergence

“KL Divergence” 라고 주로 부르는 서로 다른 두 분포의 차이 (dissimilarity) 를 측정하는데 쓰이는 measure 이다. 이를 entropy와 cross entropy 개념에 대입하면 두 entropy 차이로 계산된다. KL Divergence의 정의는 아래와 같다(아래 정의는 p와 q가 이산분포일 때 정의되는 것이며, 연속 분포일 때는 sum 대신 integral이 들어갈 것이다) 두 분포 q(실제)와 p(예측)가 있을 때

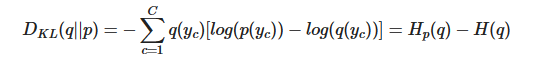
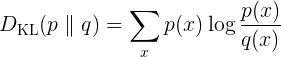
cross-entropy = H_p(q)는 실제 entropy = H(q) 보다 항상 크기 때문에 KL Divergence 는 항상 0보다 큰 값을 갖게된다. 예측 분포인p 를 실제분포 q에 가깝게 하는 것이, 예측모형이 하고자하는 것이며, p가 q에 가까이갈 수록 KL Divergence 0에 가까워질 것이다. 그리고 H(q) 는 고정이기 때문에, H_p(q)를 최소화 시키는 것이 예측 모형을 최적화 시키는 것이라고 할 수 있다. 따라서 cross-entropy 를 최소화 시키는 것이 KL Divergenece 를 최소화 시키는 것이며, 이것이 불확실성을 제어하고자하는 예측모형의 실질적인 목적이라고 볼 수 있다.