머신 러닝 훑어보기

이번에는 머신 러닝의 특징들에 대해서 배웁니다. 딥 러닝 또한 머신 러닝에 속하므로, 아래의 머신 러닝의 특징들은 모두 딥 러닝의 특징이기도 합니다.

1. 머신 러닝 모델의 평가

실제 모델을 평가하기 위해서 데이터를 훈련용, 검증용, 테스트용 이렇게 세 가지로 분리하는 것이 일반적입니다. 다만, 이 책의 목적은 개념 학습이므로 일부 실습에서는 별도로 세 가지로 분리하지 않고 훈련용, 테스트용으로만 분리해서 사용합니다. 그렇다면 훈련용, 테스트용 두 가지로만 나눠서 테스트 데이터로 한 번만 테스트하면 더 편할텐데 굳이 왜 검증용 데이터를 만들어 놓는 것일까요?

검증용 데이터는 모델의 성능을 평가하기 위한 용도가 아니라, 모델의 성능을 조정하기 위한 용도입니다. 더 정확히는 과적합이 되고 있는지 판단하거나 하이퍼파라미터의 조정을 위한 용도입니다. 하이퍼파라미터(초매개변수)란 값에 따라서 모델의 성능에 영향을 주는 매개변수들을 말합니다. 반면, 가중치와 편향과 같은 학습을 통해 바뀌어져가는 변수를 이 책에서는 매개변수라고 부릅니다.

이 두 값 하이퍼파라미터와 매개변수의 가장 큰 차이는 하이퍼파라미터는 보통 사용자가 직접 정해줄 수 있는 변수라는 점입니다. 뒤의 선형 회귀 챕터에서 배우게 되는 경사 하강법에서 학습률(learning rate)이 이에 해당되며 딥 러닝에서는 은닉층의 수, 뉴런의 수, 드롭아웃 비율 등이 이에 해당됩니다. 반면 여기서 언급하는 매개변수는 사용자가 결정해주는 값이 아니라 모델이 학습하는 과정에서 얻어지는 값입니다. 정리하면 절대적인 정의라고는 할 수 없지만, 하이퍼파라미터는 사람이 정하는 변수인 반면, 매개변수는 기계가 훈련을 통해서 바꾸는 변수라고 할 수 있으며 이 책에서는 이와 같은 기준으로 변수의 이름을 명명합니다.

훈련용 데이터로 훈련을 모두 시킨 모델은 검증용 데이터를 사용하여 정확도를 검증하며 하이퍼파라미터를 튜닝(tuning)합니다. 또한 이 모델의 매개변수는 검증용 데이터로 정확도가 검증되는 과정에서 점차 검증용 데이터에 점점 맞추어져 가기 시작합니다.

하이퍼파라미터 튜닝이 끝났다면, 이제 검증용 데이터로 모델을 평가하는 것은 적합하지 않습니다. 이제 모델은 검증용 데이터에 대해서도 일정 부분 최적화가 되어있기 때문입니다. 모델에 대한 평가는 모델이 아직까지 보지 못한 데이터로 하는 것이 가장 바람직합니다. 검증이 끝났다면 테스트 데이터를 가지고 모델의 진짜 성능을 평가합니다. 비유하자면 훈련 데이터는 문제지, 검증 데이터는 모의고사, 테스트 데이터는 실력을 최종적으로 평가하는 수능 시험이라고 볼 수 있습니다.

만약, 검증 데이터와 테스트 데이터를 나눌 만큼 데이터가 충분하지 않다면 k-폴드 교차 검증이라는 또 다른 방법을 사용하기도 합니다

2. 분류(Classification)와 회귀(Regression)

전부라고는 할 수 없지만, 머신 러닝의 많은 문제는 분류 또는 회귀 문제에 속합니다. 이 책의 머신 러닝 챕터에서는 머신 러닝 기법 중 선형 회귀(Lineare Regression)과 로지스틱 회귀(Logistic Rgression)를 다루는데 선형 회귀를 통해 회귀 문제에 대해서 학습하고, 로지스틱 회귀를 통해 (이름은 회귀이지만) 분류 문제를 학습합니다.

분류는 또한 이진 분류(Binary Classification)과 다중 클래스 분류(Multi-Class Classification)로 나뉩니다. 엄밀히는 다중 레이블 분류(Multi-lable Classification)라는 또 다른 문제가 존재하지만, 이 책에서는 이진 분류와 다중 클래스 분류만 다룹니다.

1) 이진 분류 문제(Binary Classification)

이진 분류는 주어진 입력에 대해서 둘 중 하나의 답을 정하는 문제입니다. 시험 성적에 대해서 합격, 불합격인지 판단하고 메일로부터 정상 메일, 스팸 메일인지를 판단하는 문제 등이 이에 속합니다.

2) 다중 클래스 분류(Multi-class Classification)

다중 클래스 분류는 주어진 입력에 대해서 두 개 이상의 정해진 선택지 중에서 답을 정하는 문제입니다. 예를 들어 서점 아르바이트를 하는데 과학, 영어, IT, 학습지, 만화라는 레이블이 각각 붙여져 있는 5개의 책장이 있다고 합시다. 새 책이 입고되면, 이 책은 다섯 개의 책장 중에서 분야에 맞는 적절한 책장에 책을 넣어야 합니다. 이 때의 다섯 개의 선택지를 주로 카테고리 또는 범주 또는 클래스라고 하며, 주어진 입력으로부터 정해진 클래스 중 하나로 판단하는 것을 다중 클래스 분류 문제라고 합니다.

3) 회귀 문제(Regression)

회귀 문제는 분류 문제처럼 0 또는 1이나 과학 책장, IT 책장 등과 같이 분리된(비연속적인) 답이 결과가 아니라 연속된 값을 결과로 가집니다. 예를 들어 시험 성적을 예측하는데 5시간 공부하였을 때 80점, 5시간 1분 공부하였을 때는 80.5점, 7시간 공부하였을 때는 90점 등이 나오는 것과 같은 문제가 있습니다. 그 외에도 시계열 데이터를 이용한 주가 예측, 생산량 예측, 지수 예측 등이 이에 속합니다.

3. 지도 학습(Supervised Learning)과 비지도 학습(Unsupervised Learning)

머신 러닝은 크게 지도 학습, 비지도 학습, 강화 학습으로 나눕니다. 하지만 강화 학습은 이 책의 범위를 벗어나므로 설명하지 않습니다. 또한 이 책은 주로 지도 학습에 대해서 다룹니다.

1) 지도 학습

지도 학습이란 레이블(Label)이라는 정답과 함께 학습하는 것을 말합니다. 이는 앞서 2챕터의 데이터의 분리 챕터에서 상세히 설명한 바 있습니다. 레이블이라는 말 외에도 y, 실제값 등으로 부르기도 하는데 이 책에서는 이 용어들을 상황에 따라서 바꿔서 사용합니다.

이때 기계는 예측값과 실제값의 차이인 오차를 줄이는 방식으로 학습을 하게 되는데 예측값은 y과 같이 표현하기도 합니다.

2) 비지도 학습

반면, 비지도 학습은 레이블이 없이 학습하는 것을 말합니다. 예를 들어 토픽 모델링의 LDA는 비지도 학습에 속하며, 뒤에서 배우게 되는 워드투벡터(Word2Vec)는 마치 지도 학습을 닮았지만, 비지도 학습에 속합니다.

4. 샘플(Sample)과 특성(Feature)

많은 머신 러닝 문제가 1개 이상의 독립 변수 x를 가지고 종속 변수 y를 예측하는 문제입니다. 많은 머신 러닝 모델들, 특히 인공 신경망 모델은 독립 변수, 종속 변수, 가중치, 편향 등을 행렬 연산을 통해 연산하는 경우가 많습니다. 그래서 앞으로 인공 신경망을 배우게되면 훈련 데이터를 행렬로 표현하는 경우를 많이 보게 될 겁니다. 독립 변수 x의 행렬을 X라고 하였을 때, 독립 변수의 개수가 n개이고 데이터의 개수가 m인 행렬 X는 다음과 같습니다.

이때 머신 러닝에서는 하나의 데이터, 하나의 행을 샘플(Sample)이라고 부릅니다. (데이터베이스에서는 레코드라고 부르는 단위입니다.) 종속 변수 y를 예측하기 위한 각각의 독립 변수 x를 특성(Feature)이라고 부릅니다.

5. 혼동 행렬(Confusion Matrix)

머신 러닝에서는 맞춘 문제수를 전체 문제수로 나눈 값을 정확도(Accuracy)라고 합니다. 하지만 정확도는 맞춘 결과와 틀린 결과에 대한 세부적인 내용을 알려주지는 않습니다. 이를 위해서 사용하는 것이 혼동 행렬(Confusion Matrix)입니다.

예를 들어 양성(Positive)과 음성(Negative)을 구분하는 이진 분류가 있다고 하였을 때 혼동 행렬은 다음과 같습니다. 각 열은 예측값을 나타내며, 각 행은 실제값을 나타냅니다.

이를 각각 TP(True Positive), TN(True Negative), FP(False Postivie), FN(False Negative)라고 하는데 True는 정답을 맞춘 경우고 False는 정답을 맞추지 못한 경우입니다. 그리고 Positive와 Negative는 각각 제시했던 정답입니다. 즉, TP는 양성(Postive)이라고 대답하였고 실제로 양성이라서 정답을 맞춘 경우입니다. TN은 음성(Negative)이라고 대답하였는데 실제로 음성이라서 정답을 맞춘 경우입니다.

그럼 FP는 양성이라고 대답하였는데, 음성이라서 정답을 틀린 경우이며 FN은 음성이라고 대답하였는데 양성이라서 정답을 틀린 경우가 됩니다. 그리고 이 개념을 사용하면 또 새로운 개념인 정밀도(Precision)과 재현율(Recall)이 됩니다.

1) 정밀도(Precision)

정밀도은 양성이라고 대답한 전체 케이스에 대한 TP의 비율입니다. 즉, 정밀도를 수식으로 표현하면 다음과 같습니다.

2) 재현율(Recall)

재현율은 실제값이 양성인 데이터의 전체 개수에 대해서 TP의 비율입니다. 즉, 양성인 데이터 중에서 얼마나 양성인지를 예측(재현)했는지를 나타냅니다.

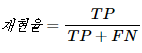
6. 과적합(Overfitting)과 과소 적합(Underfitting)

학생의 입장이 되어 같은 문제지를 과하게 많이 풀어서 문제 번호만 봐도 정답을 맞출 수 있게 되었다고 가정합시다. 그런데 다른 문제지나 시험을 보면 점수가 안 좋다면 그게 의미가 있을까요?

머신 러닝에서 과적합(Overfitting)이란 훈련 데이터를 과하게 학습한 경우를 말합니다. 훈련 데이터는 실제로 존재하는 많은 데이터의 일부에 불과합니다. 그런데 기계가 훈련 데이터에 대해서만 과하게 학습하면 테스트 데이터나 실제 서비스에서의 데이터에 대해서는 정확도가 좋지 않은 현상이 발생합니다.

예를 들어 강아지 사진과 고양이 사진을 구분하는 기계가 있을 때, 검은색 강아지 사진 훈련 데이터를 과하게 학습하면 기계는 나중에 가서는 흰색 강아지나, 갈색 강아지를 보고도 강아지가 아니라고 판단하게 됩니다. 이는 훈련 데이터에 대해서 지나친 일반화를 한 상황입니다.

과적합 상황에서는 훈련 데이터에 대해서는 오차가 낮지만, 테스트 데이터에 대해서는 오차가 높아지는 상황이 발생합니다. 아래의 그래프는 과적합 상황에서 발생할 수 있는 훈련 횟수에 따른 훈련 데이터의 오차와 테스트 데이터의 오차의 변화를 보여줍니다.

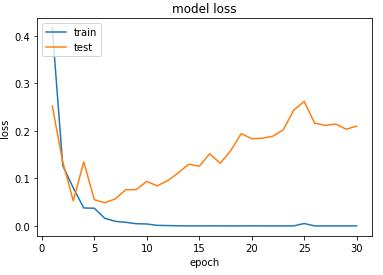
사실 위의 그래프는 10챕터에서 배우게 될 스팸 메일 분류하기 실습에서 훈련 데이터에 대한 훈련 횟수를 30회로 주어서 의도적으로 과적합을 발생시켰을 때의 그래프입니다. X축의 에포크(epoch)는 전체 훈련 데이터에 대한 훈련 횟수를 의미합니다. 앞으로 계속 나오게 될 용어이니 기억합시다.

스팸 메일 분류하기 실습은 에포크가 3~4를 넘어가게 되면 과적합이 발생합니다. 위의 그래프는 테스트 데이터에 대한 오차가 점차 증가하는 양상을 보여줍니다. 반대로 말하면 훈련 데이터에 대한 정확도는 높지만, 테스트 데이터는 정확도가 낮은 상황이라고 말할 수도 있습니다. 즉, 테스트 데이터의 오차가 증가하기 전이나, 정확도가 감소하기 전에 훈련을 멈추는 것이 바람직합니다.

과적합 방지를 위해 테스트 데이터의 성능이 낮아지기 전에 훈련을 멈추는 것이 바람직하다고 했는데, 테스트 데이터의 성능이 올라갈 여지가 있음에도 훈련을 덜 한 상태를 반대로 과소적합(Underfitting)이라고 합니다. 과소 적합은 훈련 자체가 부족한 상태이므로 과대 적합과는 달리 훈련 데이터에 대해서도 보통 정확도가 낮다는 특징이 있습니다.

이러한 두 가지 현상을 과적합과 과소 적합이라고 부르는 이유는 머신 러닝에서 학습 또는 훈련이라고 하는 과정을 적합(fitting)이라고도 부를 수 있기 때문입니다. 모델이 주어진 데이터에 대해서 적합해져가는 과정이기 때문입니다. (이러한 이유로 케라스에서는 기계를 학습시키는 도구의 이름을 fit()이라고 명명합니다.)

딥 러닝을 할 때는 과적합을 막을 수 있는 드롭 아웃(Drop out), 조기 종료(Early Stopping)과 같은 몇 가지 방법이 존재합니다.