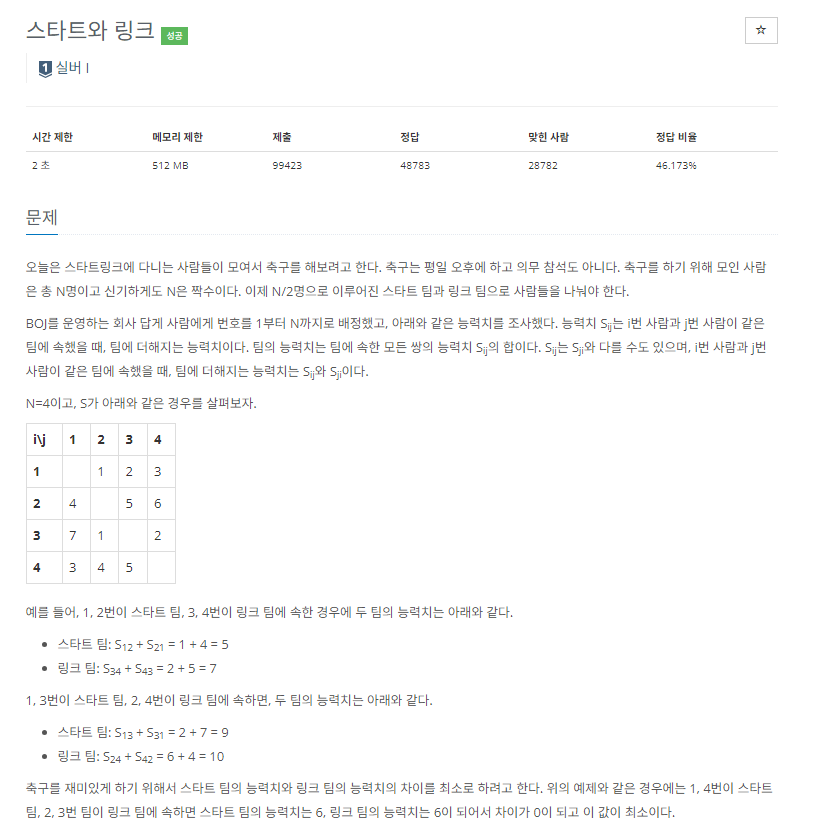
[백준] 삼성 SW 역량 테스트 기출 문제 14889번 : 스타트와 링크 (파이썬/Python)

커피넛·2024년 4월 7일

코딩 테스트

목록 보기

153/157

[백준] 삼성 SW 역량 테스트 기출 문제 14889번 : 스타트와 링크 (파이썬/Python)

정답 전체 코드

import sys
input = sys.stdin.readline

def cal_diff(start_team, link_team):
    start_power = sum([S[i][j] for i in start_team for j in start_team])
    link_power = sum([S[i][j] for i in link_team for j in link_team])
    return abs(start_power - link_power)

def backtrack(index, team):
    global min_diff
    if len(team) == n // 2:
        start_team = team
        link_team = [x for x in range(n) if x not in start_team]
        diff = cal_diff(start_team, link_team)
        min_diff = min(min_diff, diff)
        return 
    for i in range(index, n):
        if i not in team:
            team.append(i)
            backtrack(i +1, team)
            team.pop()

n = int(input())
S = [list(map(int, input().split())) for _ in range(n)]

min_diff = float('inf')

backtrack(0, [])

print(min_diff)

문제 설명

위 문제는 주어진 N명의 사람들을 두 팀으로 나누어, 각 팀의 능력치 차이를 최소화하는 문제이다. N은 짝수이고, 각 사람들 사이의 능력치는 주어진 2차원 배열에 S에 저장한다.

문제 접근 방법

모든 가능한 팀 조합을 만들기
각 조합에 대해 스타트팀과 링크 팀의 능력치 차이를 계산하고, 이 차이를 최소로 하는 값을 찾아야한다.

위 2가지를 수행하기 위해서 백트래킹 알고리즘을 사용하여 모든 가능한 팀 조합을 전부 탐색할 수 있다. 백트래킹 알고리즘은 모든 가능한 경우의 수 중에서 해를 찾는 방법으로, 중간에 답이 아닐거같은 경우 이 방법을 바로 포기하는 방법이라서 즉, 되돌아가서 Backtrack 이라고 불린다.

알고리즘 설명

차이 계산 함수 cal_diff 는 주어진 두 팀 조합의 각 팀 능력치를 계산하고 두 팀의 차이를 절대값으로 바꾸어 반환한다.
백트래킹 함수에서 특정 인덱스에서 시작하여 가능한 모든 팀 조합을 생성하고, 팀이 N/2 으로 구성되었을 때, 스타트 팀과 링크 팀의 능력치 차이를 계산하고, 이 차이를 최솟값을 업데이트한다.
전역 변수 min_diff 스타트 팀과 링크 팀의 능력치 차이의 최솟값을 저장한다. 초기합은 inf 로 무한대로 설정한다.
N과 S를 입력받고, backtrack 함수를 호출하여 모든 가능한 팀 조합을 전부 탐색한다. 마지막에 min_diff 를 출력한다.

코드 설명

첫째 줄에 N을 입력받고, 이후 N개의 줄에 걸쳐 2차원 배열 S를 입력받는다.
cal_diff 함수는 두 팀의 인덱스 리스트를 인자로 받아, 해당 팀의 능력치를 계산하고 두 팀의 능력치 차이를 반환한다.
backtrack 함수는 현재 인덱스와 현재까지 구성된 팀의 리스트를 인자로 받는다. 함수 내에서, 팀이 N/2명으로 채워지면 스타트 팀과 링크 팀의 능력치 차이를 계산하고 min_diff를 업데이트한다. 그렇지 않은 경우, 현재 인덱스부터 시작하여 다음 사람을 팀에 추가하고 백트래킹을 계속 진행한다.