[프로그래머스 코딩테스트 2017 팁스타운] 예상 대진표 | 알고리즘 설명 & 문제 풀이 with 자바스크립트(Javascript)

1. 문제 설명

2. 제한 사항

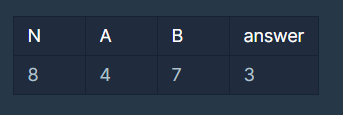
3. 입출력 예

4. 입출력 예 설명

5. 첫번째 문제 풀이(2023-12-11)

이 문제는 한 경기가 치뤄질 때마다 전체 인원의 반이 줄어드는 특징이 있습니다. 즉 N이 8(8명) 일때 한 경기를 치를 경우 인원은 4가 되는 것이고, 또 한 경기를 치루면 인원은 2가 되는 것이기에 이 속성을 이용해서 각각 A 선수와 B 선수를 경기가 치뤄질 때마다 2로 나누면 됩니다.

입출력 설명을 보면 A 선수의 처음 번호는 4번 이였는데 경기를 치룰 때마다 2번, 1번이 됩니다. 즉 4/2 와 2/1 의 값인 셈이죠.

B 선수도 마찬가지입니다. 7에서 4가 되고, 4에서 2가 되는 식으로 짝수로 이어갑니다.

문제는 해당 선수(B)가 홀수일 경우인데, 메서드 중에 실수를 반올림 처리 해주는 round와 ceil가 있어서 저는 무엇을 쓸까 고민을 했는데, 물론 2로 나누는 거라 실수가 5 미만이 나오긴 어렵지만(5 미만일 경우 round를 써도 반올림이 안되기에) 그래도 혹시 몰라서 부동소수점의 값 상관 없이 무조건 반올림을 시켜주는 ceil 메서드를 사용했습니다.

B의 선수에게 ceil 메서드를 적용시킬 경우 처음은 7/2 = 3.5가 나오는데, ceil 메서드를 사용하므로 4가 됩니다. 그리고 다시 4/2 = 2가 되는 형식인거죠.

function solution(n, a, b) {
    var answer = 0;

    while(n) { // 어차피 if문에 걸리면 break를 걸거라 while를 n으로 잡았습니다.
        if(b !== a){ // 두 선수의 값을 계속 2로 나누어 반올림(ceil) 하다 보면 1을 사이에 두고 만나는 경우가 발생이 된 다음 값이 같아지는 경우가 발생 되므로 그 때는  만난 횟수를 카운트 하는 조건은 두 선수의 값이 같아지기 전까지로 설정하면 됩니다.
            a = Math.ceil(a / 2);
            b = Math.ceil(b / 2);
            answer++;    
        }else break; // 두 선수의 값이 같아진 경우, 즉 서로 만난 다음 쇼부가 정해진 다음이라면 while문을 종료시키고
    };

    return answer; // 값을 반환.
}