[프로그래머스 코딩테스트 기초] 등차수열의 특정한 항만 더하기 | 알고리즘 설명 & 문제 풀이 with 자바스크립트(Javascript)

1. 문제 설명

2. 제한 사항

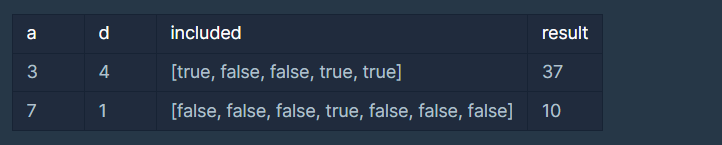
3. 입출력 예

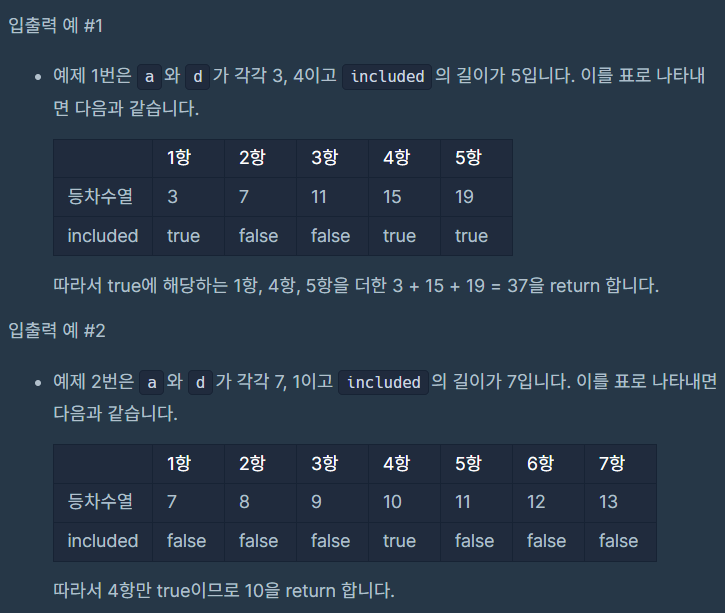
4. 입출력 예 설명

5. 첫번째 문제 풀이(2023-12-20)

이번 문제는 우선적으로 항을 구한 후 included의 i번째 값이 true일때 해당 항을 result에 누적 증가시키는 방법으로 풀었습니다.

이 문제를 풀면서 저번에 등차수열, 등비수열을 구했던 공식이 생각나 응용을 해보았는데, 등차수열을 구할 경우 차이(gap)에 i의 값을 곱하고 그 결과값을 처음 값(a)에 더하면 차수를 구할 수 있다고 하더군요. 신기했습니다...!

function solution(a, d, included) {

    let result = 0;
 
    for(let i = 0; i < included.length ; i++){
        let term = a + d * i // 차수 구하기
        result += included[i] === true ? term : 0 // included의 현재 값이 true일 때 차수를 누적
    }
    return result //차수 반환
}