[프로그래머스 코딩테스트 연습문제] N개의 최소공배수 | 알고리즘 설명 & 문제 풀이 with 자바스크립트(Javascript)

1. 문제 설명

2. 제한 사항

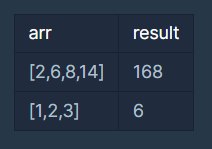
3. 입출력 예

4. 첫번째 문제 풀이(2023-12-12)

일전에 풀었던 연습 문제에서 최대공약수를 구하는 알고리즘을 직접 작성해 봤는데, 구글링을 하다보니 삼항 연산자와 재귀 함수 조합으로 유클리드 호제법을 구현해낸 분이 있어서 그 분의 코드를 참고하게 되었습니다.

그리고 for문 문제는 도저히 이해가 가지를 않아서 gpt에 물어봤는데, 문제의 뜻은 말 그대로 배열 안의 요소들의 공통된 최소공배수를 찾아야 한다는 것이었습니다.

어떤 말이냐면, [2,6,8,14] 배열에서 2와 6의 최소공배수를 먼저 찾은 후 그 최소공배수와 8의 공통된 최소공배수를 찾고, 또 거기서 도출 된 최소공배수와 14의 공통된 최소공배수를 찾을 때 배열 안의 요소에서의 공통된 최소공배수가 나올것이라는 말이었습니다.

아래의 코드의 실행 순서는 다음과 같습니다.

1. 최대공약수를 구하는 공식에 삼항연산자와 재귀 함수의 조합을 이용하여 함수를 구현
2. 반환 된 최대공약수를 이용해 최소공배수를 구하는 함수를 구현
3. lcm(최대공약수)를 구하는 함수가 호출되면 분모에 배치되어 있는 최대공약수를 구하는 호출을 또 호출합니다.
4. a에 2, b에 6이 할당되어 전달되었다고 해봅시다. 첫번째 getGCD에서 b는 0이 아니므로 재귀 함수가 호출되는데, b를 a에, a를 b로 나눈 나머지의 값을 b에 전달합니다.
5. 다시 a는 6이 되고, b는 2를 6으로 나눈 나머지인 6이 할당되어 6,2의 모습을 보입니다. 즉 처음 getLCM 문과 달리 반전이 된 모습이죠.
6. 그 상태에서 b(2)도 0이 아니므로 다시 재귀 함수를 호출하는데 이때에는 2(b)가 a쪽으로, a(6)을 b(2)로 나누고 난 나머지 값(0)이 전달되므로 결과적으로 2(a), 0(b)가 전달됩니다.
7. 이제 b는 0이므로 2와 6의 최대공약수는 2(a)가 되어 반환되고 최대공약수를 구하는 함수는 종료됩니다.
8. 다시 최소공배수를 구하는 함수로 돌아와 a와 b를 곱한 값에 반환된 최대공약수로 나눈 값을 얻고 반환된 후 해당 함수도 종료됩니다.
9. lcm에는 반환된 값인 최소공배수가 할당되고 그 다음 for문을 반복하며 실질적으로 배열 중 2와 6의 최소공배수와 6 다음의 값(8)의 최소공배수를 구하게 되는 것이죠.
10. 여기서 최대공약수를 구하는 로직의 첫번째 호출은 a가 b보다 작을 경우 무조건 이 둘을 반전(큰 수로 작은 수를 나눌 경우 나머지는 작은수가 되기 때문에)되는 효과를 만들 수 있습니다.

function solution(arr) {
    // 최소공배수 계산 함수
    const getLCM = (a, b) => (a * b) / getGCD(a, b);

    // 최대공약수 계산 함수 (유클리드 호제법)
    const getGCD = (a, b) => (b === 0 ? a : getGCD(b, a % b)); // 전달 받은 인자 중 b가 0(최소공약수가 나타나는 시점)일때 a(b가 0인 시점에서의 최소공약수 a)를 반환하고, 아닐 경우에는 최소공약수 함수를 재귀 호출하여 b의 값을 a에 받고, a%b의 값을 b에 받도록 전해줍니다. 이후 해당 루프를 반복.

    // 배열의 숫자들을 순차적으로 최소공배수 계산
    let lcm = arr[0];
    for (let i = 1; i < arr.length; i++) {
        lcm = getLCM(lcm, arr[i]);
    }

    return lcm; // for문이 끝난 후 최종적으로 반환 된 최소공배수를 return.
}