[프로그래머스 코딩테스트 연습문제] 점프와 순간 이동 문제 풀이 with 자바스크립트(Javascript) & 자바(Java)

Re_Go·2024년 7월 5일

목록 보기

93/98

1. 첫번째 문제 풀이(2024-07-05)

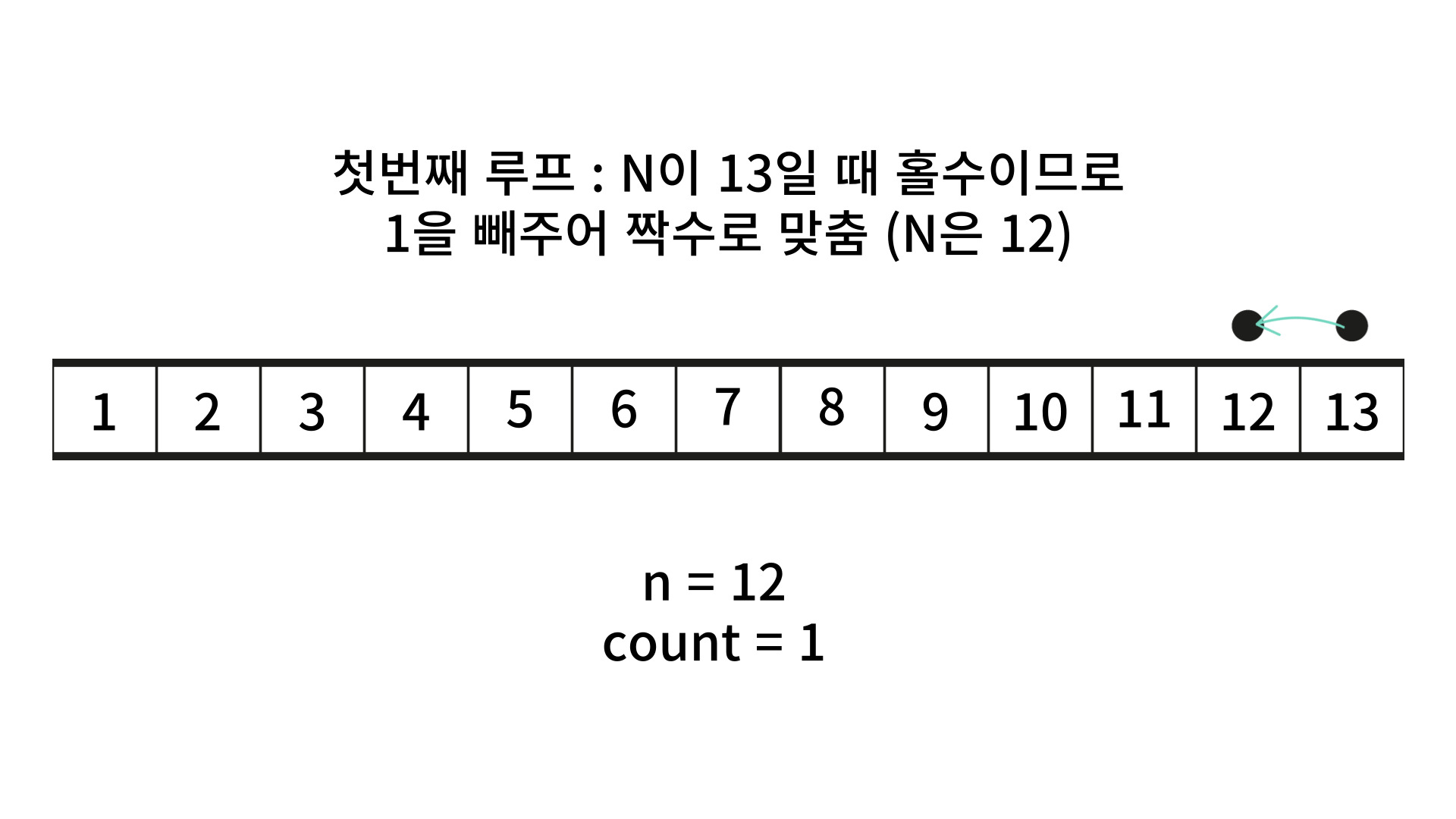
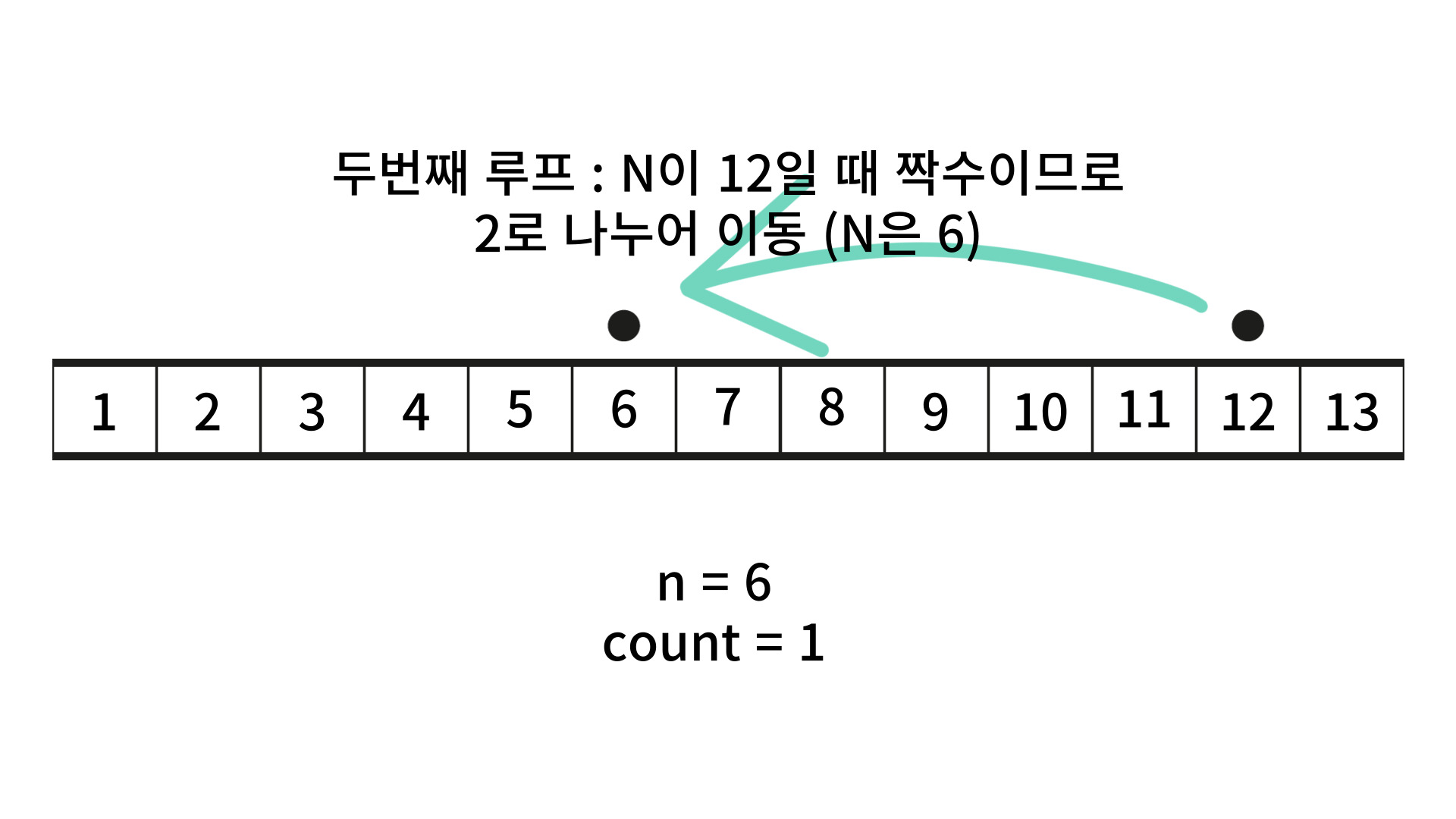
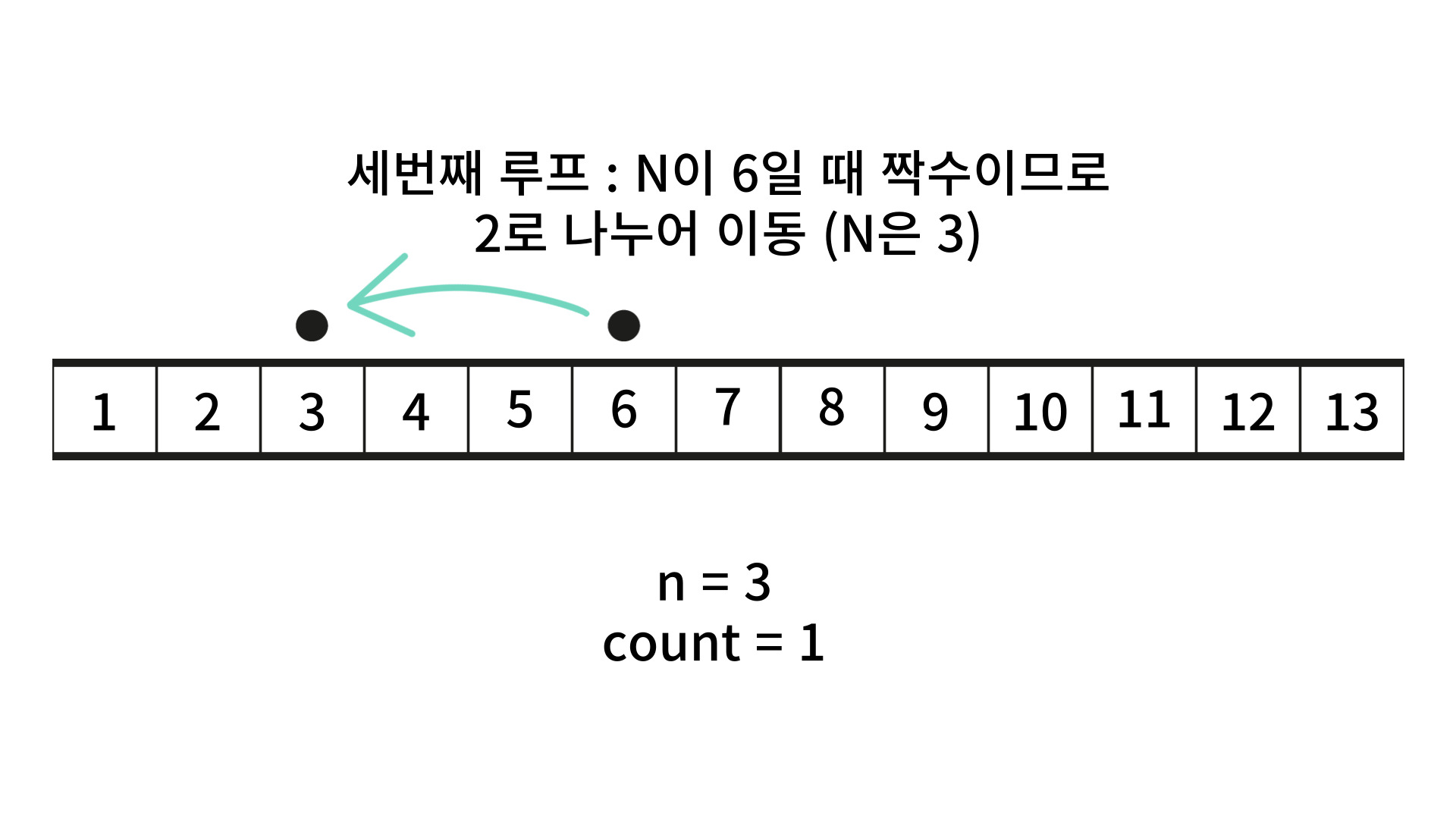
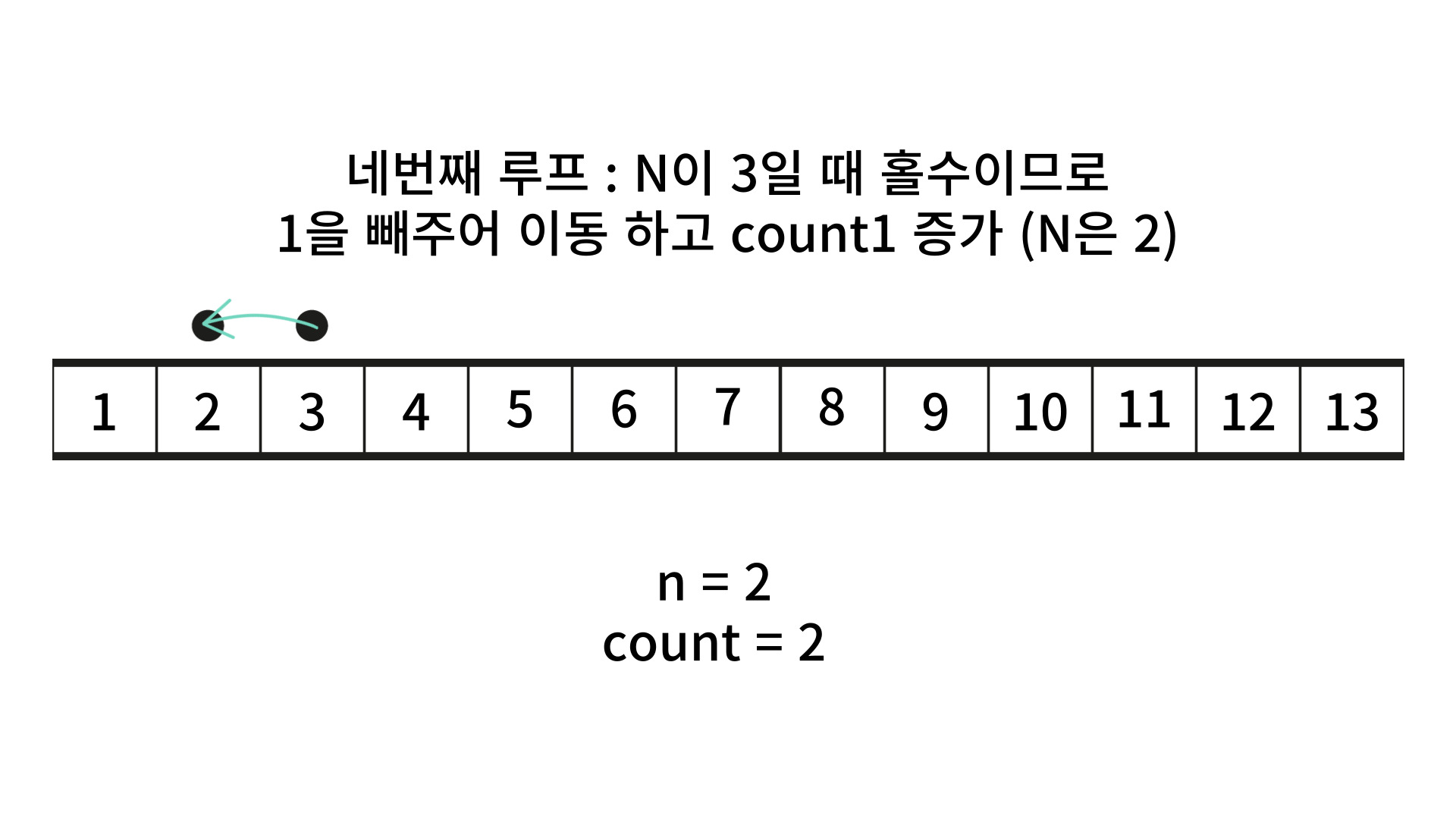
해당 문제는 Lv2 짜리라 그런지 좀 많이 벅차더라고요 🤣 그래서 구글링을 좀 해봤는데요. 짝수일 때 2를 나누고, 홀수일 때 현재 n의 값을 -1로 만들어서 짝수로 맞춰주고, 이동값을 1 늘려주면 해결이 된다고 하더군요.

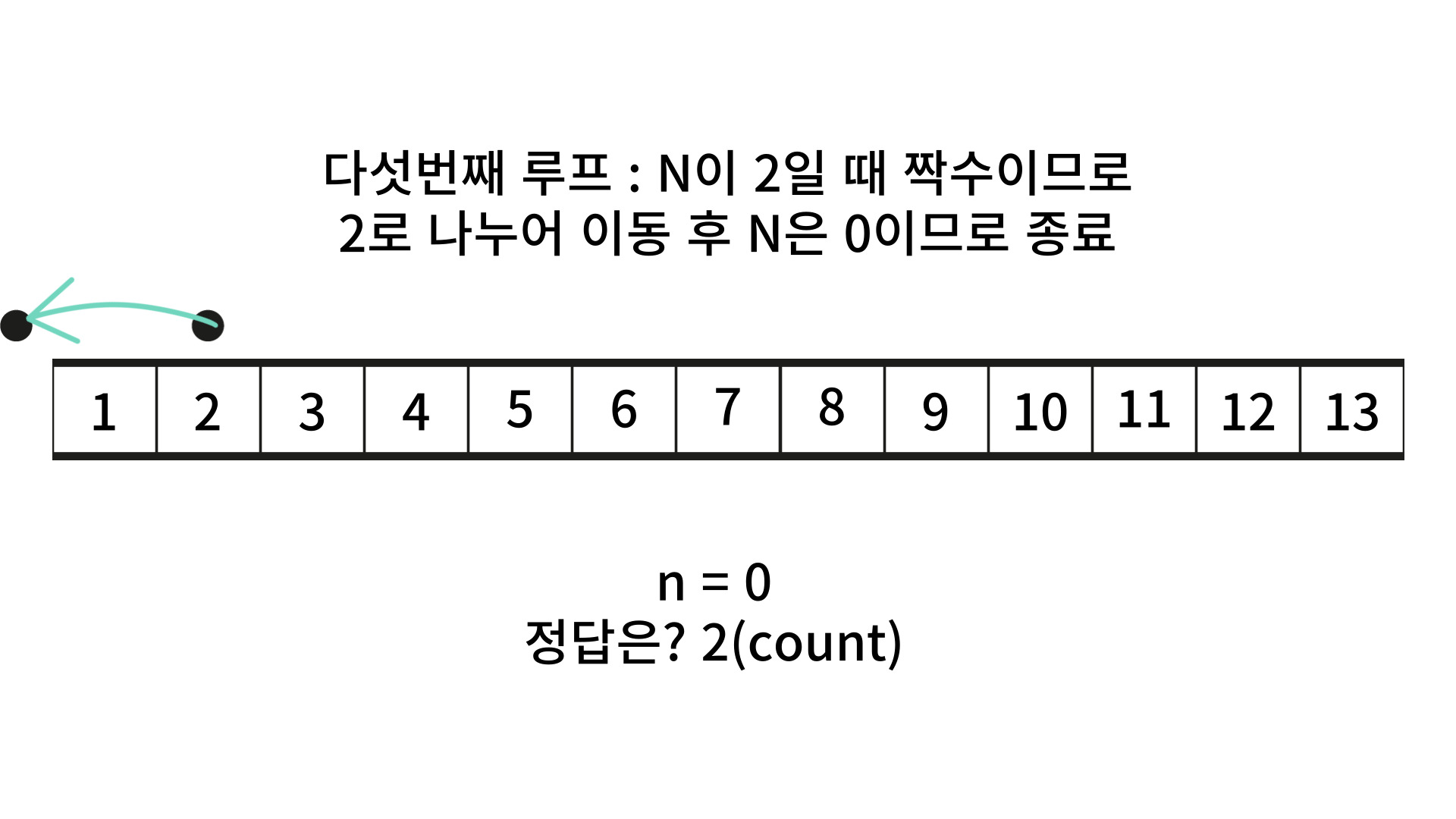
그래서 계산을 해봤더니, 신기하게도 곱하기로 접근하여 풀고자 했던 방법보다 이 방법이 더 잘 이해가 되더라고요! 그래서 그림으로 그려서 그 원리를 설명해 보고자 합니다.

(자료 출처 : 미리캔버스로 만들어 봤습니다 ㅎ...)

아무튼 이런 원리라고 하는데요. 그렇다면 다음부터는 최적의 해를 구할 때 굳이 2 뿐만이 아니더라도 n만큼 일정하게 이동하는 경우 또 써먹을 수 있을 것 같더라고요! (물론 점프하는 값 k나 순간이동의 범위가 달라지면 또 그만큼 홀수 구간에서 k만큼 빼주고 짝수 구간에서 순간이동의 범위 만큼 나눈 나머지를 구하면 되겠지요.)

근데 특이하게 해당 문제는 2진법으로도 푸는게 가능하더라고요. 일전에 풀었던 문제에서 만들었던 함수(2진법으로 변환된 문자열의 1의 개수를 구해주는 함수)를 이용해 봤는데 신기하게도 동일하게 풀려지더랍니다!

근데 원리는 몰라서 그냥 먼저 소개한 원리가 저한테는 더 나은 듯 합니다 ㅎ... 😅

아무튼 해당 알고리즘을 적용한 JS 코드를 보여드리면 다음과 같습니다.
자바스크립트 버전
// 1. 앞전에 소개한 짝수와 홀수 분기점을 이용한 최적의 해로 푼 코드 (그림 참조 ㅎ...)
function solution(n) {
    let count = 0;
    let nowPosition = n; // 목표 지점부터 출발

    while (nowPosition > 0) {
        if (nowPosition % 2 === 0) {
            nowPosition /= 2;
        } else {
            nowPosition--;
            count++ ;
        }
    }
    return count;
}

// 2. 2진법의 1의 개수를 구하는 함수를 이용해 점프를 한 횟수를 구하는 코드
function solution(n) {
    let count = 0;
    let nowPosition = n; // 목표 지점부터 출발

    while (nowPosition > 0) {
        if (nowPosition % 2 === 0) {
            nowPosition /= 2;
        } else {
            nowPosition--;
            count++ ;
        }
    }
    return count;
}
그리고 자바 버전으로 구현한 코드는 다음과 같습니다.
자바 버전
// 1. 최적의 해 자바 버전 (이하 생략
import java.util.*;

public class Solution {
    public int solution(int n) {
        int count = 0;
        int nowPosition = n; // 목표 지점부터 출발

        while (nowPosition > 0) {
            if (nowPosition % 2 == 0) {
                nowPosition /= 2;
            } else {
                nowPosition--;
                count++;
            }
        }
        return count;
    }
}

// 2. 2진수 구하는 메서드를 이용해 점프 횟수를 구하는 자바 코드 버전
public class Solution {
    public int solution(int n) {
        int count = 0;
        int nowPosition = n; // 목표 지점부터 출발

        while (nowPosition > 0) {
            if (nowPosition % 2 == 0) {
                nowPosition /= 2;
            } else {
                nowPosition--;
                count++;
            }
        }
        return count;
    }
}