1. 문제 설명
두 수를 입력받아 두 수의 최대공약수와 최소공배수를 반환하는 함수, solution을 완성해 보세요. 배열의 맨 앞에 최대공약수, 그다음 최소공배수를 넣어 반환하면 됩니다. 예를 들어 두 수 3, 12의 최대공약수는 3, 최소공배수는 12이므로 solution(3, 12)는 [3, 12]를 반환해야 합니다.
2. 제한 사항
두 수는 1이상 1000000이하의 자연수입니다.
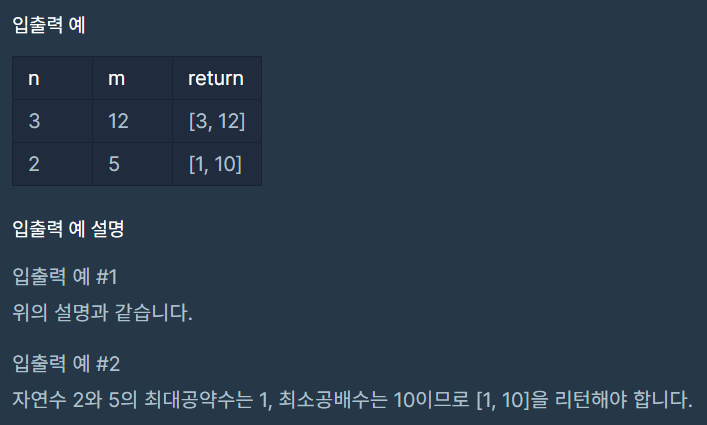
3. 입출력 예 설명
4. 첫번째 문제 풀이(2023-12-09)
일단 최대공약수와 최소공배수에 대한 개념은 구글에서 서칭한 후에 알았는데, 어떻게 구해야 할지 몰라서 다음의 블로그를 참고했는데요. 유클리드 호제법은 고대 그리스 수학자인 유클리드라는 학자가 만들어낸 수학 공식중 하나이고, 호제법이란 두 수를 나누어 원하는 답을 얻는 알고리즘이라고 합니다.
즉 유클리드가 창안해 낸 알고리즘중 하나인거죠. (알고싶지 않다...)
일단 위의 블로그에서 설명하고 있는 최대공약수를 구하는 공식은 a와 b를 나눌 때 나오는 r로 다시 b를 나눌 때 0으로 떨어지는 시점에서의 b의 값이라고 합니다. 무슨 말이냐면 만약 67와 128이라는 숫자가 있다고 가정을 했을 때
- 128(a) % 67(b) = 61(r)에서 나누어 떨어지지 않으므로 r에는 a%b의 결과값을, a에는 b의 값을, b에는 다시 r의 값을 할당합니다.
- 67(a) % 61(b) = 6(r) 에서도 마찬가지로 나누어 떨어지지 않으므로 위와 같은 작업 반복
- 61(a) % 6(b) = 1(r) 에서 마찬가지.
- 6(a) % 1(b) = 0(r) 에서 나머지는 비로소 0이 되므로 이때 b는 1이므로 최대공약수는 1이라는 것이죠.
그리고 블로그의 설명에 따르면 최소공배수를 구하는 공식은 a와 b를 곱한 값을 a와 b의 최대공약수로 나눈 값이라고 하네요. 결과적으로 이 문제는 최대공약수만 구하면 쉽게 해결이 되는 문제였습니다.
function solution(n, m) {
var answer = [lcd(n,m), lcm(n,m)]; //저는 편하게 함수 호출로 배열을 채웠습니다. (어차피 호이스팅이 되니...)
function lcd(n,m){ // 앞에서 설명 드린 내용대로 테스트 케이스는 n(작은 값)과 m(큰 값) 으로 입력되기 때문에 최소공약수를 구하는 공식에서는 큰 값을 작은 값으로 나누는 나머지를 구해야 하니 m과 n의 위치를 스위칭 시켜줬습니다.
while(n !== 0){
tmp = m%n;
m = n;
n = tmp
};
return m; // 앞서 말씀드린 것처럼 나머지(tmp)가 0이 될때 b(여기서는 m)는 최소공약수가, n에는 결과값(0)이 저장되기 때문에 m을 반환해줍니다.
};
function lcm(n,m){
return (n*m) / lcd(n,m); // 최소공배수는 앞서 설명한 것처럼 주어진 두 수의 곲을 두 수의 최대공약수로 나눈 결과값이므로 다음 표현식의 결과를 리턴해 줍니다.
};
return answer;
}