출처: 백준 온라인 저지
https://www.acmicpc.net/problem/1051
틀린 풀이
고안한 알고리즘은 다음과 같다.
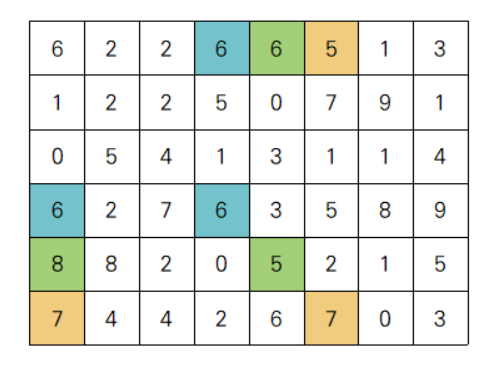
숫자들이 주어졌을 때, 각 숫자를 왼쪽 위 꼭짓점으로 가지는 정사각형들을 조사하여, 정사각형의 크기가 가장 큰 것을 구한다. 예를 들어, 숫자들이 위와 같이 주어졌다고 하자. 위의 배열을 arr라고 할 때, arr[0][0]의 6에서부터, 해당 수를 왼쪽 위 꼭짓점으로 가지는 정사각형을 조사한다.
가장 큰 정사각형부터 조사한다. arr[0][0]을 왼쪽 위 꼭짓점으로 가지는 가장 큰 정사각형은 arr[0][0], arr[0][5], arr[5][0], arr[5][5]다. 이 세 개의 수가 모두 6이라면, arr[0][0]을 왼쪽 위 꼭짓점으로 가지는 가장 큰 정사각형을 찾은 것이다. 아니라면 다음으로 길이를 1씩 줄여가며 네 꼭지점의 수가 모두 같은 정사각형을 찾는다. 위에서는 arr[0][0], arr[0][3], arr[3][0], arr[3][3]의 수가 모두 같다. 그렇다면 arr[0][0]을 왼쪽 위 꼭짓점으로 가지는 가장 큰 정사각형의 크기는 16이다.
from sys import stdin
n, m = map(int, stdin.readline().split())
boards = []
for _ in range(n):
boards.append([int(x) for x in stdin.readline().rstrip()])
max_square = [[0] * (m - 1) for _ in range(n - 1)]
for r in range(n - 1):
for c in range(m - 1):
x = boards[r][c]
i = min(n - r, m - c) - 1
while i > 0 and not max_square[r][c]:
if boards[r][c + i] == x and boards[r + i][c] == x and boards[r + i][c + i] == x:
max_square[r][c] = (i + 1) * (i + 1)
i -= 1
max_value = 0
for r in range(n - 1):
max_value = max(max_value, max(max_square[r]))
print(max_value)하지만 위의 코드는 2가지 문제가 있었다.
문제 해결 과정
문제 1
문제에서는 "꼭짓점에 쓰여 있는 수가 모두 같은 가장 큰 정사각형"을 찾아야 한다고 했다. 그래서 당연히 4개의 수에 의해 만들어지는 정사각형만을 고려했다. 하지만 하나의 수는 그 자체로 수가 모두 같은 꼭짓점을 가지는 정사각형이었다. 사실 이 부분은 문제에서 명확히 밝히지 않는 부분도 있다.
문제 2
문제 1을 해결하고 나니 ValueError가 떴다. 문제는 max(max_square[r]) 부분에 있었다.
위 코드에서는 boards[r][c]를 왼쪽 위 꼭짓점으로 가지는 가장 큰 정사각형을 max_square[r][c]에 저장하고, 마지막에 이 배열의 가장 큰 값을 max_value에 저장한다. 그런데 만약 처음 주어지는 숫자의 행 수인 m이 1이라면, max_square의 각 행에는 빈 리스트가 들어가게 된다. 빈 리스트를 max 함수 안에 넣어서 ValueError가 발생하게 된 것이다.
max 함수에 빈 리스트를 넣어보면 아래와 같은 문구가 나온다.
ValueError: max() arg is an empty sequence
위의 2가지 문제를 해결한 코드는 아래와 같다.
from sys import stdin
n, m = map(int, stdin.readline().split())
boards = []
for _ in range(n):
boards.append([int(x) for x in stdin.readline().rstrip()])
max_square = [[1] * (m - 1) for _ in range(n - 1)]
for r in range(n - 1):
for c in range(m - 1):
x = boards[r][c]
# (r, c)를 왼쪽 위 꼭짓점으로 가지는 가장 큰 정사각형의 크기 지정
i = min(n - r, m - c) - 1
while i > 0 and max_square[r][c] == 1:
if boards[r][c + i] == x and boards[r + i][c] == x \
and boards[r + i][c + i] == x:
max_square[r][c] = (i + 1) * (i + 1)
i -= 1
max_value = 1
for r in range(n - 1):
for c in range(m - 1):
max_value = max(max_value, max_square[r][c])
print(max_value)최종 풀이
시간 줄이기
위 코드에서는 마지막 행, 마지막 열을 제외한 모든 수에 대하여, 그 수를 왼쪽 위 꼭지점으로 가지는 가장 큰 정사각형의 크기를 구한다. 하지만 사실 배열 전체에서 가장 큰 정사각형의 크기를 구하는 것이므로 그렇게 할 필요는 없다.
아래 코드에서는 max_square 배열을 따로 만들지 않고, 가장 큰 정사각형의 크기를 나타내는 dist 변수만을 주었다.
arr[r][c], arr[r + i][c], arr[r][c + i], arr[r + i][c + i]로 이루어지는 정사각형을 발견하면, i의 값을 dist에 저장한다. 그 이후에는 dist보다 큰 i에 대해서만 위의 정사각형을 탐색하면 된다. dist보다 작거나 같은 i에 대하여 또 다른 정사각형을 발견하더라도, 배열 전체에서 가장 큰 정사각형의 크기는 변하지 않기 때문이다.
위 내용을 구현한 코드는 아래와 같다.
from sys import stdin
n, m = map(int, stdin.readline().split())
arr = []
for _ in range(n):
arr.append([int(x) for x in stdin.readline().rstrip()])
dist = 0
for r in range(n - 1):
for c in range(m - 1):
x = arr[r][c]
# (r, c)를 왼쪽 위 꼭짓점으로 가지는 가장 큰 정사각형의 크기 지정
i = min(n - r, m - c) - 1
while i > dist:
if arr[r][c + i] == x and arr[r + i][c] == x \
and arr[r + i][c + i] == x:
dist = i
i -= 1
print((dist + 1) * (dist + 1))