출처: 백준 온라인 저지
https://www.acmicpc.net/problem/11727
처음 풀이
2 x n 타일을 채우는 방법의 수를 f(n)이라고 하자. 2 x n 타일을 채우는 방법은 3가지로 나눌 수 있다.
- 오른쪽 끝을
2 x 1타일로 채우는 경우 - 오른쪽 끝을
1 x 2타일 2개로 채우는 경우 - 오른쪽 끝을
2 x 2타일로 채우는 경우
①의 경우 다시 2 x (n-1) 타일을 채워야 한다.
②, ③의 경우 다시 2 x (n-2) 타일을 채워야 한다.
따라서 f(n) = f(n-1) + 2 * f(n-2)의 등식이 성립하게 된다.
# 동적 프로그래밍을 이용한 풀이
from sys import stdin
n = int(stdin.readline())
tile_list = [1, 1]
for i in range(2, n + 1):
tile_list.append(tile_list[i - 1] + 2 * tile_list[i - 2])
print(tile_list[n] % 10007)점화식을 활용한 풀이
앞선 항들의 값을 통해 다음 항의 값이 정해지는 관계를 점화 관계라고 한다. 특히 이전 항의 배수들의 합으로 다음 항의 값이 정해질 때, 이 관계를 선형 점화 관계라고 한다. 중요한 점은, 선형 점화 관계에서는 초기 조건만 주어지면 점화 관계의 일반 해를 구할 수 있다는 점이다.
이를테면, 피보나치 수열에서 n번째 수를 F(n)이라고 하면, F(n) = F(n - 1) + F(n - 2)의 점화식이 성립하며, 이는 선형 점화 관계이므로 일반항을 구할 수 있다.
참고 : 피보나치 수열의 일반항
마찬가지로 2xn 타일을 채우는 방법의 수를 f(n)이라고 할 때, f(n)의 일반항을 구할 수 있다. f(n)에 대해서는 아래의 내용이 성립한다.
f(n) = f(n-1) + 2 * f(n-2)f(1) = 1,f(2) = 3
그리고 이를 통해 이 성립함을 알 수 있다. 그래서 아래와 같은 짧은 풀이가 가능해진다.
# 일반항을 이용한 풀이
n = int(input())
print(((2 ** (n + 1) + (-1) ** n) // 3) % 10007)물론 애초에 문제에서 요구하는 것이 동적 프로그래밍이기도 하고, 위 수식을 구현하느니 동적 프로그래밍 코드를 구현하는 것이 더 나을 것이다. 다만, 동적 프로그래밍의 기반이 되는 점화 관계에서 일반항을 구할 수 있다는 사실을 알아두면 좋을 것 같다.
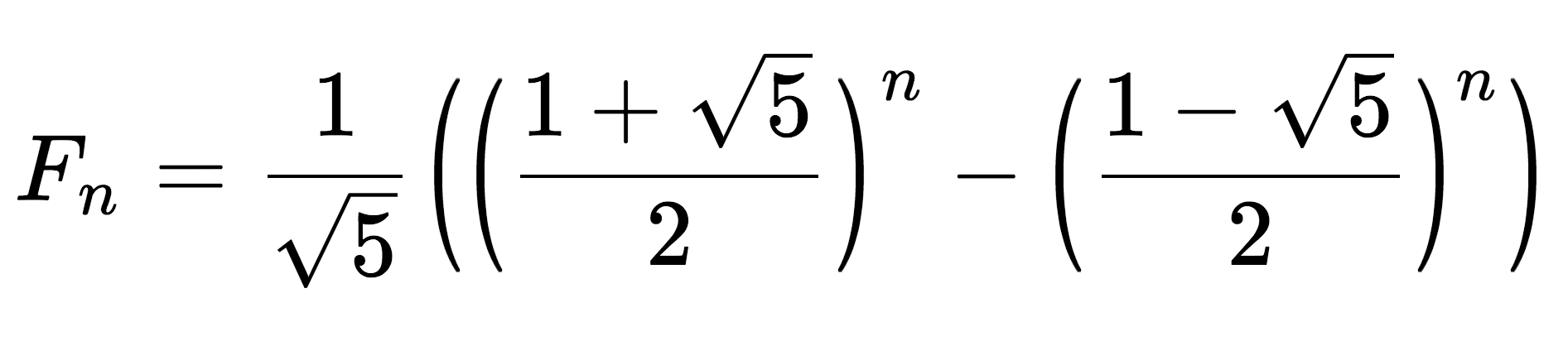

거의 모든 타일 채우기 문제는 일반항을 세우는 것이 가능하다고 합니다..!