[Python] 백준 - 2565 전깃줄

출처: 백준 온라인 저지
https://www.acmicpc.net/problem/2565

문제 설명

두 전봇대 A와 B 사이에 연결된 두 전깃줄 $t1$, $t2$가 있다고 하자. 이때 두 전깃줄이 겹치지 않는 조건은 다음과 같다.

• 전봇대 A에서 $t1$ < $t2$라면, 전봇대 B에서도 $t1$ < $t2$다.
• 전봇대 A에서 $t1$ > $t2$라면, 전봇대 B에서도 $t1$ > $t2$다.

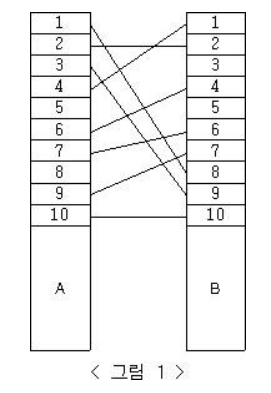
전깃줄들이 위에서 서술한 조건을 만족하기 위해서는, 전봇대 A의 번호에 따라 오름차순 정렬했을 때, 전봇대 B의 번호들도 증가수열이 되어야 한다.

예를 들어, 위 그림에서 전봇대 A의 번호에 따라 오름차순으로 나열하면 (1, 8), (2, 2), (3, 9), (4, 1)...이 될 것이다. 8 > 2이므로 (1, 8)과 (2, 2)는 공존할 수 없지만, 2 < 9이므로 (2, 2), (3, 9)는 공존할 수 있다.

결국 겹치지 않는 전깃줄의 최대 개수는, 전봇대 A의 번호를 기준으로 정렬했을 때, 전봇대 B의 번호를 나열한 수열의 부분 증가 수열의 최대 길이와 같다. <그림 1>에서는 [8, 2, 9, 1, 4, 6, 7, 10]의 부분 증가 수열의 최대 길이가 [2, 4, 6, 7, 10]의 5이므로, 전깃줄은 최대 5개가 남아있을 수 있다.

따라서 이 문제는 LIS 알고리즘으로 풀 수 있다.

최종 풀이

from sys import stdin


n = int(stdin.readline())

lines = []

for _ in range(n):
    a, b = map(int, stdin.readline().split())

    lines.append((a, b))

lines.sort()

# a 전깃줄 번호를 기준으로 오름차순 정렬된 b 전깃줄 번호의 수열
a_to_b = list(map(lambda x: x[1], lines))

# LIS 알고리즘 구현
max_length = [1] * n

for i in range(1, n):
    for j in range(i):
        if a_to_b[i] > a_to_b[j]:
            max_length[i] = max(max_length[i], max_length[j] + 1)

# 없애야 하는 전깃줄의 최소 개수 = 현재 전깃줄의 개수 - 겹치치 않는 최대 전깃줄의 개수
print(n - max(max_length))