Hi There 👋
이번 포스트에는 Generative model에 대한 기본 정의와 이를 이해하기 위한 통계 이론, 그리고 Generative model을 사용한 알고리즘을 정리해보려고 한다.
Generative model (생성모델)이란
-
Generative model이란 단순 이미지를 생성하는 것으로 생각하는 경우가 많다. (Generation (sampling))
여기서 generation을 하기 위해선 을 따르는 를 sampling한다. -
하지만 단순 모델을 생성하는 것 뿐만 아니라 이미지가 주어졌을때, 이 이미지를 구분하는 anomaly detection도 포함되어 있다.
이걸 explicit model이라고 부른다. (Density estimation) -
아직 많은 논란이 있지만 generative model에 Unsupersived representation learning 도 포함된다. (feature learning)
그렇다면 결국엔 generation을 하기 위해선 를 정의해야하는데 어떻게 찾을 수 있을까 고민해야한다.
그 전에 우리는 기본적인 통계 지식이 있어야 한다. 바로 밑에 필요한 내용을 정리하겠다.
Basic Distributions
Parameter 수를 어떻게 줄일까

이런 2차원 binary image가 있다. (pixel 개수는 n, pixel이 모두 서로 dependence하다고 가정)
하나의 이미지를 만들기 위한 경우의 수는 한 픽셀에서 0 or 1의 상태를 가질 수 있으므로 이다.
우리가 에서 이미지를 sampling하기 위해선 몇 개의 parameter 개수가 필요한지 알아보자면, 개의 parameter가 필요하다.
모든 pixel이 dependence하기 때문에 n-1개의 pixel이 정해지면 나머지 1개의 pixel은 자동적으로 정해지기 때문이다.
하지만 딥러닝에서 parameter수가 많아지면 학습이 어렵기 때문에 parameter수를 줄여야한다.
어떻게 parameter수를 줄여야 할까?
여기서 두번째 가정이 필요하다.
만약 모든 pixel이 서로 independence하다면 어떨까?
하나의 이미지를 만들기 위한 경우의 수는 한 pixel에서 0 or 1의 상태를 가질 수 있으므로 dependence한 경우와 같이 이다.
하지만 parameter수는 exponential로 줄어든다. 모든 pixel이 independence하므로 각 pixel에 대한 parameter만 있어도 된다.
그러면 pixel의 개수는 이므로 parameter수도 으로 정해진다.
결국 dependence → independence로 가정을 변경하면 → 으로 parameter 수가 대폭 감소한다.
이러면 딥러닝 학습에 수월해져 좋은 성능을 얻을 수 있다.
하지만 모든 pixel이 independence하다는건 있을 수 없는 일이다.
여기서 말하고 싶은건 우리는 최대한 dependence와 independence의 중간 지점을 찾아 최적의 parameter 수를 정해야한다는 것이다.
Conditional Independence
위에서 우리는 parameter 수를 줄이기 위한 기초 이론에 대해서 알아봤으면,
여기선 적절한 parameter수를 가진 distribution을 찾는 trick을 설명하려고 한다.
여기서 사용할 가장 중요한 3가지 rule이 있다.
- Chain rule
- Bayes' rule
- Conditional independence
만약 Chain rule을 사용했을때, 필요한 parameter수는 몇 개일까?
- : 1 parameter
- : 2 parameters (, )
- : 4 parameters (, , ,)
이런 식으로 은 의 parameters 가 필요하다.
결국, Chain rule을 사용했을때, 필요한 parameter 수는 개의 parameter가 필요하다.
이건 위에서 dependence할때 parameter수와 같다.
여기서 만약 위에서 보여준 것과 같이 independence 가정을 추가해보자.
Markov assumption (바로 이전 데이터와 dependence하고 그 이전 데이터와 independence함)을 사용해보면,
Conditional independence에 따라서 Chain rule은 아래와 같이 식이 변경된다.
이 식에서 필요한 parameter 수를 구해보자면,
- : 1 parameter
- : 2 parameters (, )
- : 2 parameters (, )
위 내용을 보면 전부 2 parameters를 갖게되고 전체 parameter수는 개이다.
결국, independence 가정을 사용하면 parameter 개수를 exponential reduction할 수 있다.
따라서, 우리는 Chain rule과 conditional independence를 활용해서 parameter수를 최대한 줄일 수 있는 Sweet spot을 찾아야 한다.
Auto-regressive model은 이러한 conditional independency에 영향을 받는 모델이다. 바로 뒤에서 살펴보자
Auto-regressive Model (자기 회귀 모형)

이러한 28*28 binary pixel이 있다고 가정하자
우리의 목표는 를 학습하는 것이다.
그러면 우리는 어떻게 를 학습하기 위해서 parametrize를 할까?
우리는 여기서 chain rule을 사용해야 한다.
이게 autoregressive model이고 우리는 또 한가지 생각해야 할게 있다.
2차원인 이미지 데이터를 어떻게 1차원으로 ordering 해야하는 건 쉽지 않다.
ordering하는 방법이 달라지면 성능 및 많은 것이 달라지므로 잘 생각할 필요가 있다.
그럼 Auto-regressive Model을 활용한 NADE (Neural Autoregressive Density Estimator)를 살펴보자
NADE (Neural Autoregressive Density Estimator)
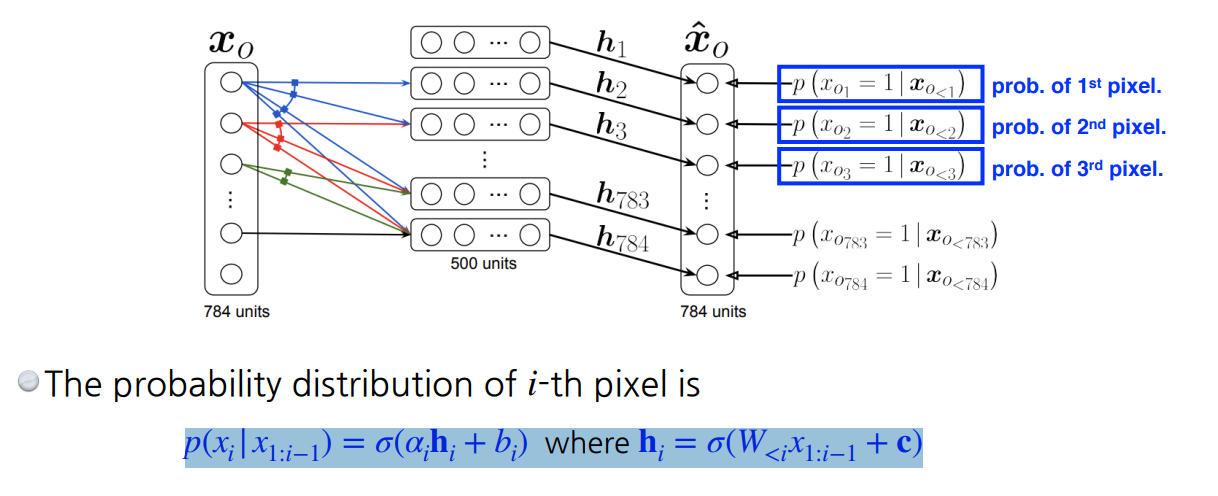
NADE의 기본 가정은 이렇다.
번째 pixel은 번째 pixel에 dependence하다.
첫번째 pixel은 모든 픽셀에 대해서 independence하게 만들고 두번째 픽셀은 첫번째 pixel에 dependence하게 만든다.
→ 첫번째 pixel값을 입력값으로 받는 Neural Network를 만들어서 sigle scalar 값을 받아 sigmoid를 통해 0~1사이 값으로 변환
그리고 번째 pixel은 개의 입력값을 받는다.
이게 Neural Network입장에서는 입력 차원이 계속 증가한다. 이 의미는 weight가 계속 증가한다는 것이다.
NADE는 explicit model이여서 입력값에 따른 확률을 계산할 수 있다.
한번 계산해보자면, (784개의 binary pixel)
또한 만약 continuous random variable 경우에는 mixture of Gaussian이 사용된다.
Pixel RNN
이때까지 Auto-regressiv Model에 대해서 정리했다.
Pixel RNN은 RNN을 사용해서 generation하는 모델이다. (기존에는 fc-layer를 통해서 생성)
예를 들면, n*n RGB 이미지가 있을때,
- : Prob. i-th R
- : Prob. i-th G
- : Prob. i-th B
이 에 따라 이미지를 Generate할 수 있다.
Pixel RNN에는 ordering하는 방법에 따라 2가지 모델 구조가 있다.
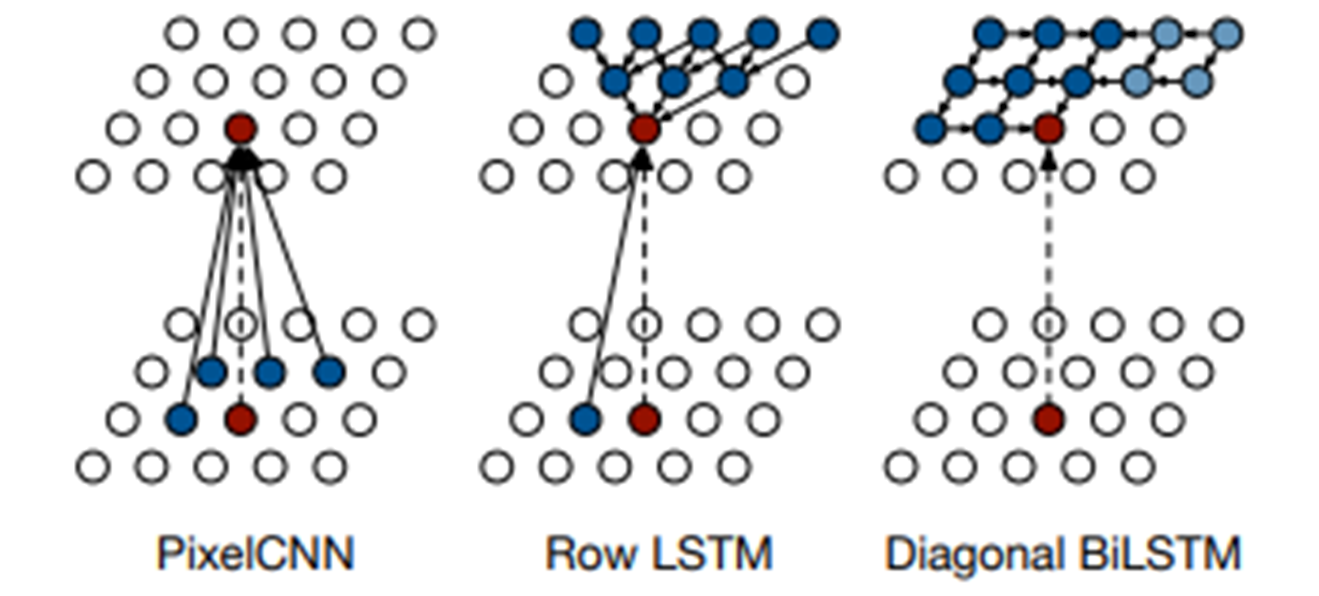
- Row LSTM : i-th pixel을 만들때, 위쪽 정보를 활용
- Diagonal BiLSTM : i-th pixel을 만들때, 이전 정보를 모두 활용
Conclusion
이번 포스트에는 Generative model에 기초적인 내용을 정리해 보았다.
다음 포스트에는 대표적인 Generative model인 GAN을 살펴보려고 한다.