[CS50] 4. 알고리즘

찐새·2022년 3월 1일

cs50 부스트코스

CS50

목록 보기

5/6

(1) 검색 알고리즘

컴퓨터는 배열에 저장된 데이터의 인덱스를 하나씩 찾아가며 그 값에 접근한다. 특정 값에 대한 탐색은 정렬 여부에 따라 다음과 같은 알고리즘을 사용할 수 있다.

(1)-1 선형 탐색

unkown array

어떤 값이 어디에 들어있는지 모르는 0번부터 6번의 사물함에서 50을 찾는다고 가정하자. 정렬 여부도 알 수 없다. 이 상태에서 최선의 방법은 0번 사물함부터 하나씩 열어가며 안에 든 내용물을 확인하는 것이다.

이렇게 인덱스 번호를 하나씩 증가시켜가며 순차적으로 찾는 알고리즘이 선형 탐색(Linear Search)이다.

(1)-2 이진 탐색

이번에는 임의의 숫자가 정렬되어 있는 상태에서 50을 찾아보자. 어떤 숫자들인지 알지 못해도 정렬이 되어 있으므로 우리는 확인한 숫자와 찾는 숫자의 크기를 비교할 수 있다. 예를 들어, 확인한 숫자가 30이라면, 50은 이보다 오른쪽에 있을 것이다. 이러한 점을 이용해 사물함의 가운데를 확인한 후 50보다 크다면 왼쪽을 찾고, 작다면 오른쪽을 찾는다.

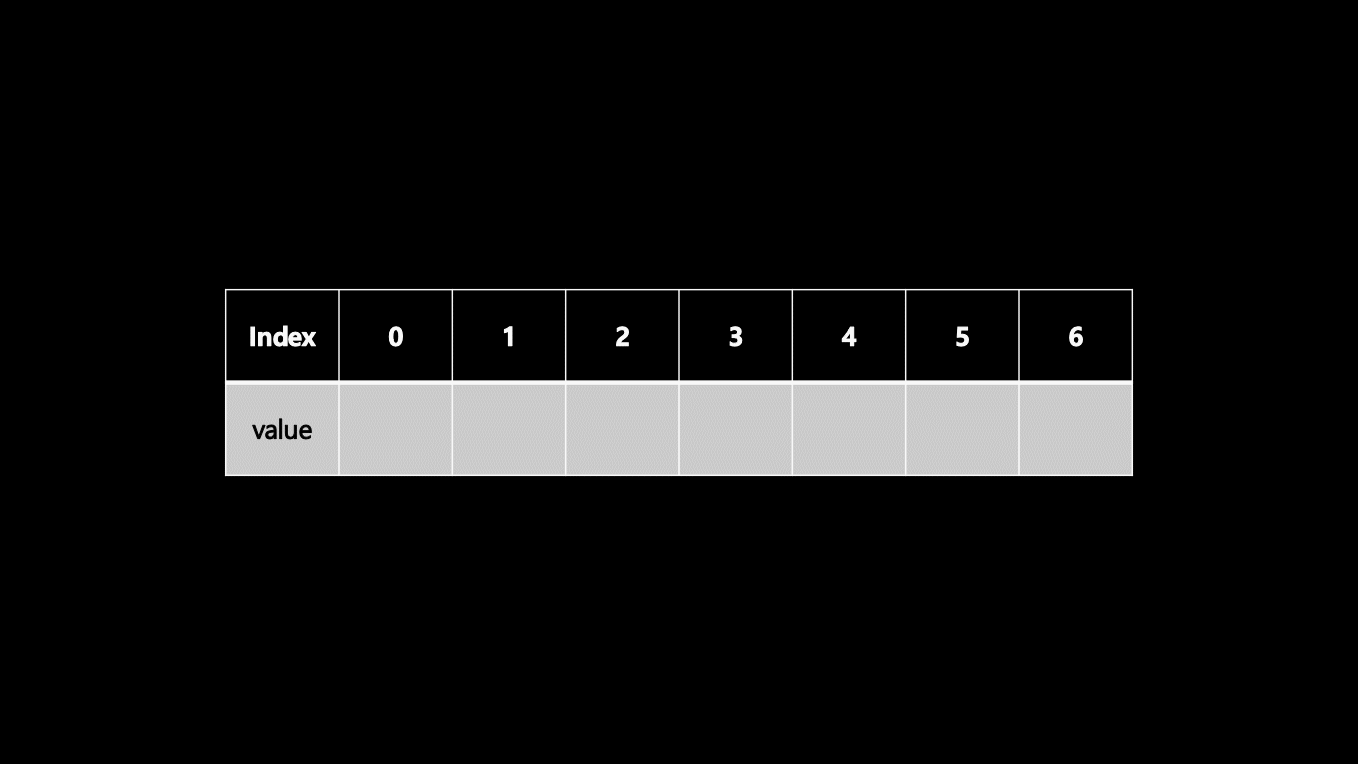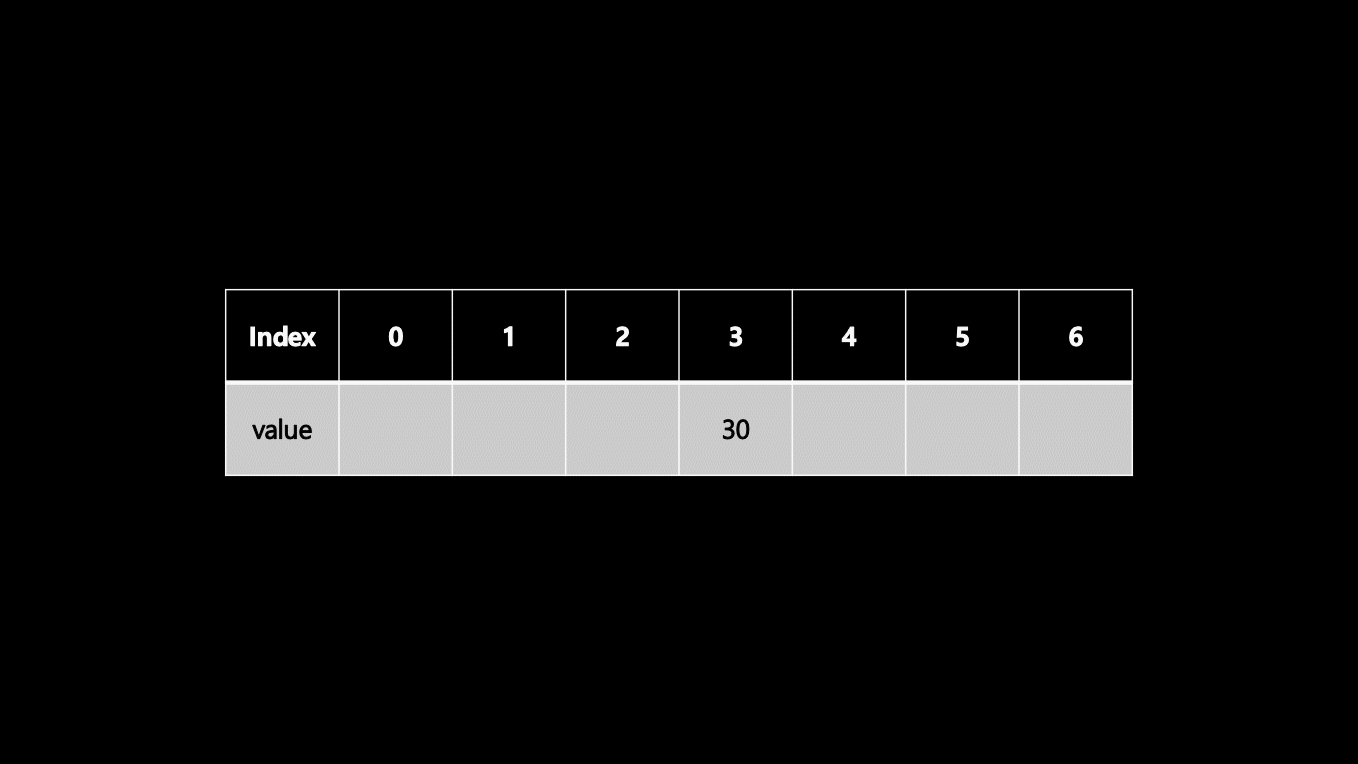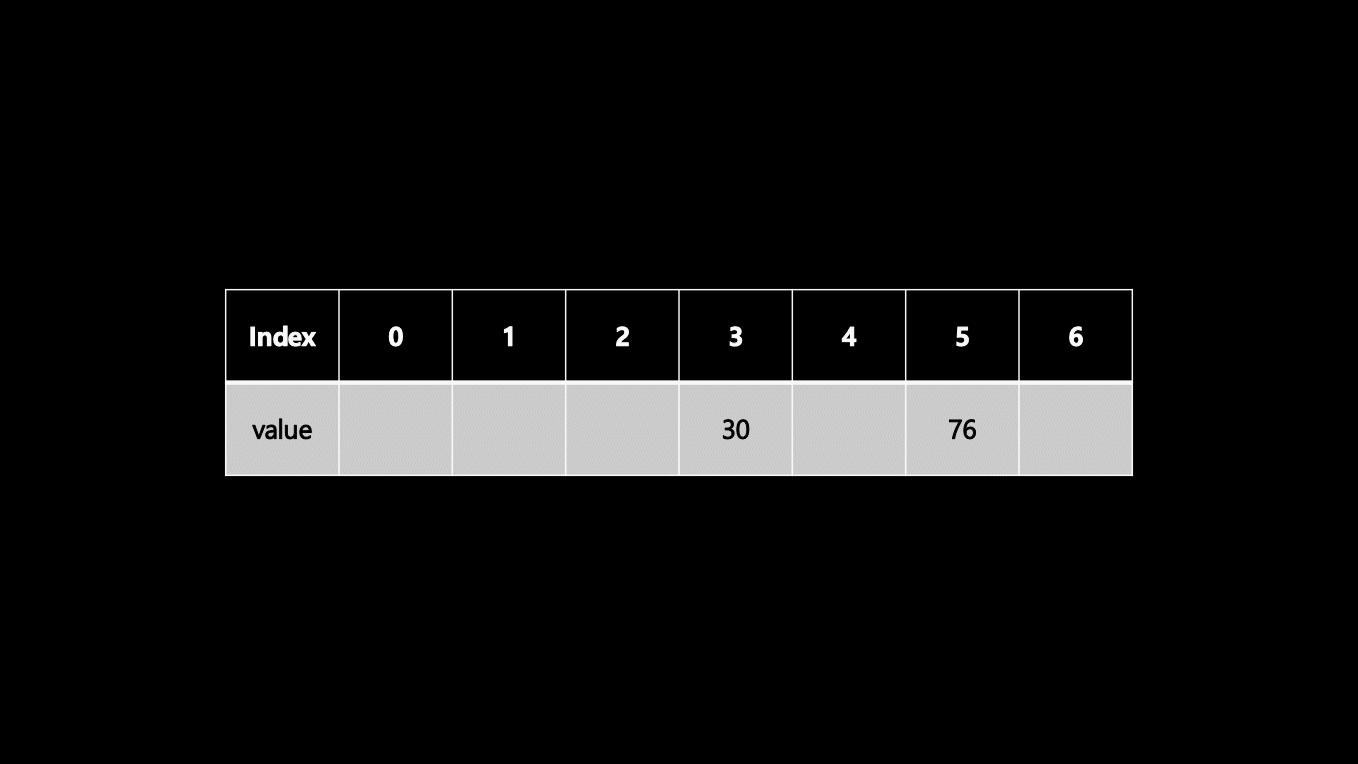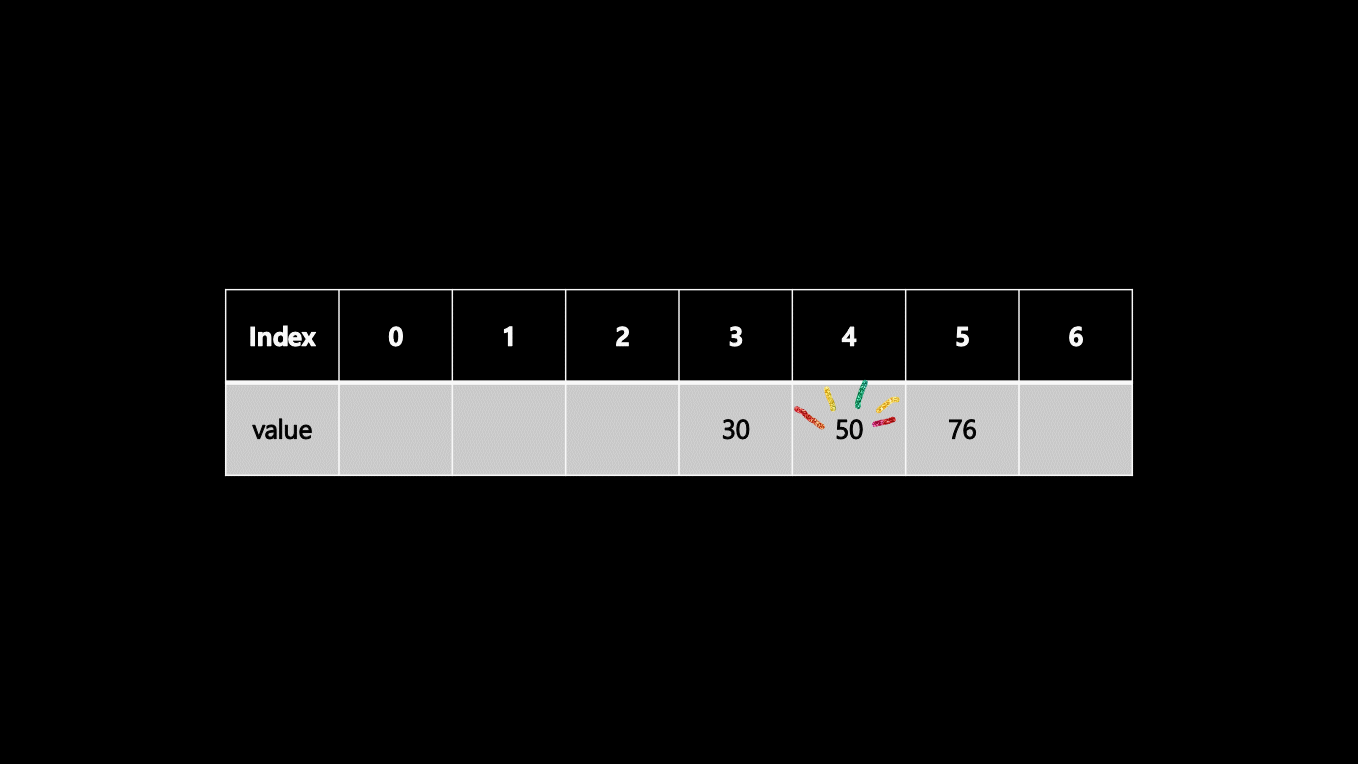
이진 탐색(Binary Search) 알고리즘은 특정한 값을 찾을 때까지 배열을 두 부분으로 분류한다.

선형 탐색과 이진 탐색 중 어떠한 것이 우세한 지는 상황에 따라 다르다. 정렬이 되어 있지 않다면 이진 탐색은 의미가 없다. 반대라면, 선형 탐색은 비효율적이다.

(2) 알고리즘 표기법

어떤 알고리즘의 효율을 판단하려면 특유의 척도를 알아둘 필요가 있다. 크게 Big O(빅오)와 Ω(오메가) 표기법 두 가지로 구분하며, 알고리즘의 시간 복잡도를 의미한다.

Big O는 최악의 경우 걸리는 시간을 나타내는 척도다.

위에서 살펴본 선형 탐색과 이진 탐색을 예로 들면, 전자의 최악은 찾고자 하는 값이 배열의 맨 끝에 있는 경우이다. n개의 사물함이 있다면 n번을 찾아야 한다. 이를 Big O로 표기하면 O(n)이 된다.

후자는 어떤 경우가 되었든 찾는 범위가 계속 반으로 줄어든다. n개의 사물함일 때 n/2/2/2/2…로 log₂ n에 수렴한다. 이때 밑은 생략하여 O(log n)으로 표기한다.

여기서 log의 밑뿐 아니라 상수도 마찬가지로 생략한다. 홀수 개씩 찾았다고 해서 O(2n+1)이 되는 게 아니라 O(n)으로 표기한다. 그 이유는 스케일업을 하면 상수가 있건 없건 그래프의 기울기가 비슷해지기 때문이다.

Ω는 반대로 최선의 경우를 나타낸다. 선형 탐색이나 이진 탐색이나 제일 좋을 때는 처음 위치에 찾는 숫자가 있을 때이다. 한 번이면 끝나므로 Ω(1)의 척도를 갖는다. 선형 탐색과 비슷하지만 총 개수를 세는 알고리즘은 최악이든 최선이든 언제나 n번 걸려 O(n), Ω(n)으로 표기한다.

여러 알고리즘 표기법이 있지만, 기본적인 것만 정리해보자.

Big O	알고리즘	Ω	알고리즘
O(n2)	-	Ω(n2)	-
O(n log n)	-	Ω(n log n)	-
O(n)	선형 탐색	Ω(n)	하나씩 세는 경우
O(log n)	이진 탐색	Ω(log n)	-
O(1)	-	Ω(1)	선형 탐색, 이진 탐색

표시하지 않은 부분은 아래에서 채울 예정이다(물론 몰라서 안 채워지는 곳도 있다.).

(3) 정렬

탐색을 효율적으로 하려면 정렬이 잘 되어 있어야 한다. 정렬의 방법에는 여러 종류가 있고, 각각 시간 복잡도를 가지고 있다. 강의에서는 버블 정렬, 선택 정렬, 병렬 정렬을 다뤘다.

(3)-1 버블 정렬

버블 정렬은 두 개의 인접한 자료 값을 비교하면서 위치를 교환하는 방식으로 정렬이다. [4, 2, 3, 1]의 배열을 오름차순 정렬한다면,

4 2 3 1 <- 첫 번째와 두 번째를 비교한다. 2가 4보다 작으므로 교환한다.
2 4 3 1 <- 두 번째와 세 번째를 비교한다. 3이 4보다 작으므로 교환한다.
2 3 4 1 <- 세 번째와 네 번째를 비교한다. 1이 4보다 작으므로 교환한다.
2 3 1 4 <- 1회전 결과

2 3 1 4
2 3 1 4
2 1 3 4
2 1 3 4 <- 2회전 결과

2 1 3 4
1 2 3 4
1 2 3 4
1 2 3 4 <- 3회전 결과. 종료

3회전 2행에서 끝나야 하는 게 아닌가 싶지만, 컴퓨터는 array[i]와 array[i+1]이 어떤 차이가 있는지 열어보지 않고는 알 수 없기 때문에 끝까지 진행한다. 때문에 버블 정렬의 시간 복잡도는 O(n²), Ω(n²)이 된다.

Big O	알고리즘	Ω	알고리즘
O(n2)	버블 정렬	Ω(n2)	버블 정렬
O(n log n)	-	Ω(n log n)	-
O(n)	선형 탐색	Ω(n)	하나씩 세는 경우
O(log n)	이진 탐색	Ω(log n)	-
O(1)	-	Ω(1)	선형 탐색, 이진 탐색

(3)-2 선택 정렬

선택 정렬은 '배열 안의 자료 중 가장 작은 수(혹은 가장 큰 수)를 찾아 첫 번째 위치(혹은 가장 마지막 위치)의 수와 교환해주는 방식의 정렬'로 '교환 횟수를 최소화하는 반면 각 자료를 비교하는 횟수는 증가'한다. [3, 4, 2, 1]를 오름차순으로 정렬해보자.

3 4 2 1 <- 가장 작은 수를 찾는다.
1 4 2 3 <- 1의 자리인 가장 첫 번째 위치와 교환한다. (1회전)
1 4 2 3 <- 다음으로 작은 수를 찾는다.
1 2 4 3 <- 2의 자리인 두 번째 위치와 교환한다. (2회전)
1 2 4 3 <- 다음으로 작은 수를 찾는다.
1 2 3 4 <- 3의 자리인 세 번째 위치와 교환한다. (3회전)
1 2 3 4 <- 교환할 숫자가 없으므로 종료한다.

선택 정렬 역시 교환할 숫자의 유무를 전부 훑어야 하는 정렬 알고리즘이다. 버블 정렬과 마찬가지로 O(n²), Ω(n²)의 시간 복잡도를 갖는다.

Big O	알고리즘	Ω	알고리즘
O(n2)	버블 정렬 선택 정렬	Ω(n2)	버블 정렬 선택 정렬
O(n log n)	-	Ω(n log n)	-
O(n)	선형 탐색	Ω(n)	하나씩 세는 경우
O(log n)	이진 탐색	Ω(log n)	-
O(1)	-	Ω(1)	선형 탐색 이진 탐색

(3)-3 병합 정렬

마지막 병합 정렬은 이진 탐색과 결이 비슷하다. 원소가 한 개가 될 때까지 계속해서 반으로 나누다가 다시 합쳐나가며 정렬이다. 이번에 숫자를 좀 늘려서 [7, 4, 5, 2, 6, 3, 8, 1]을 오름차순으로 정렬해보자.

7, 4, 5, 2 6, 3, 8, 1 <- 배열을 절반으로 나눈다.
7, 4 5, 2 6, 3, 8, 1 <- 왼쪽 절반을 다시 절반으로 나눈다.
7 4 5 2 6, 3, 8, 1 <- 왼쪽 절반의 원소가 하나가 될 때까지 나눈다.
4, 7 2, 5 6, 3, 8, 1 <- 나눈 절반을 정렬한 후 합친다.
2, 4, 5, 7 6, 3, 8, 1 <- 나눈 절반을 정렬한 후 합친다.
2, 4, 5, 7 6, 3 8, 1 <- 오른쪽을 진행한다.
2, 4, 5, 7 6 3 8 1
2, 4, 5, 7 3, 6 1, 8
2, 4, 5, 7 1, 3, 6, 7
1, 2, 3, 4, 5, 6, 7, 8 <- 전체를 정렬 후 합친다.

과정을 요약하면 아래와 같다.

7 4 5 2 6 3 8 1 <- 원소가 1개가 될 때까지 나눈 결과.
4, 7 2, 5 3, 6 1, 8 <- 1개씩 정렬하여 합친 결과
2, 4, 5, 7 1, 3, 6, 8 <- 2개씩 정렬하여 합친 결과
1, 2, 3, 4, 5, 6, 7, 8 <- 4개씩 정렬하여 합친 결과

'어떻게 합칠 때 제자리를 찾아 들어가는 거지?'라는 의문이 생겼었다. 우문이었다. '합친 후 정렬'이 아니라 '정렬 후 합침'이기 때문에 값의 위치를 컴퓨터가 기억하고 있어 빠르게 정렬되는 것이었다.

해당 정렬의 경우 시간 복잡도는 O(n log n), Ω(n log n)이 걸린다. 반으로 나누는 데에 log n의 시간이 걸리고, 합치는 데 n의 시간이 걸리기 때문이다.

Big O	알고리즘	Ω	알고리즘
O(n2)	버블 정렬 선택 정렬	Ω(n2)	버블 정렬 선택 정렬
O(n log n)	병합 정렬	Ω(n log n)	병합 정렬
O(n)	선형 탐색	Ω(n)	하나씩 세는 경우
O(log n)	이진 탐색	Ω(log n)	-
O(1)	-	Ω(1)	선형 탐색 이진 탐색