Sample 표본의 개념
-
sample
- 데이터 n개를 임의추출한 set
- 이런 sample을 여러 개 생성하여 활용
-
sample size n
- sample 한 개에 들어있는 데이터의 수.
- (e.g.) 20개의 데이터가 들어있는 sample을 100개 생성했다면, sample size는 20이다.
-
sample mean
- 한 개의 sample에서 구한 mean.
- 이 자체로 하나의 RV이 되는 경우가 많다.
-
sample variance
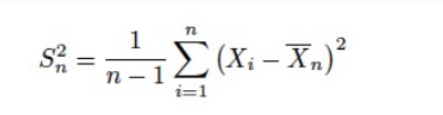
표준편차 비교
: Sample Standard Deviation, sample 1개의 표분편차
: 모분산, Standard Deviation, 원래 데이터 X의 표준편차
: 표본평균 간의 표준편차(일종의 Standard Error. SE의 개념은 다음 포스트 참고.) -
theorem
- if Xs are IID
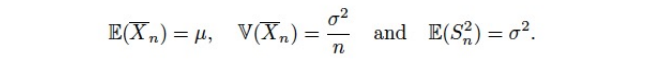
IID 란?
독립 항등 분포. 즉, 모든 변수들이 서로 독립이며 동일한 Distribution을 가진다.
- if Xs are IID
Converge(수렴) 개념
수렴 개념을 이용해서 표본평균과 표본분산을 통해, 모평균과 모분산을 구할 수 있다.
-
Definition

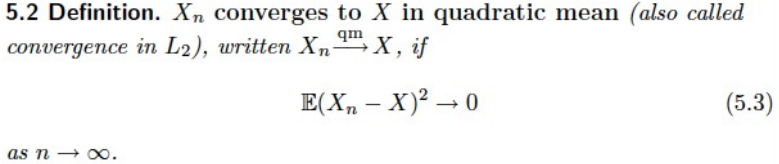
-
위 정의들 간의 관계
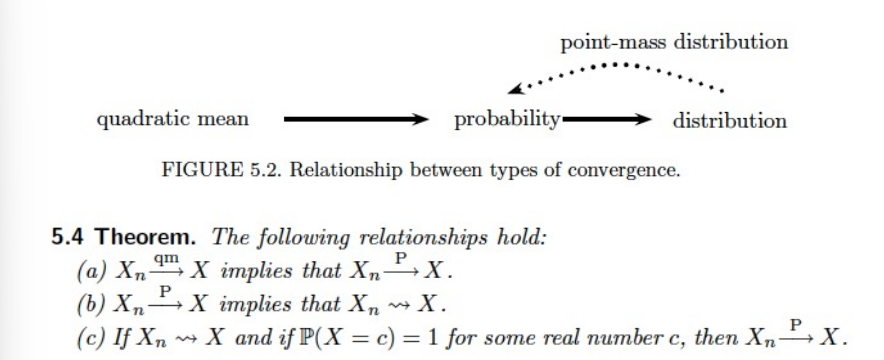
-
Property
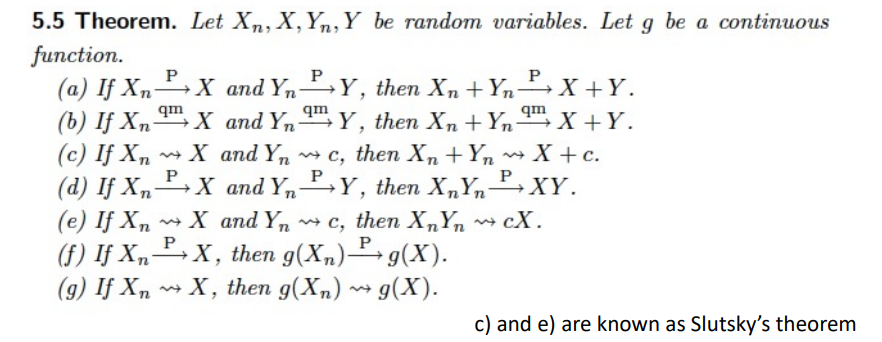
Law of large number
- The Weak Law of Large Number(WLLN)
- sample size 가 커질수록, sample mean은 mean에 수렴한다.
(sample mean의 distribution은 variance가 줄어든다.
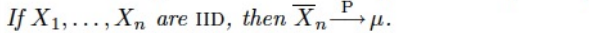
- sample size 가 커질수록, sample mean은 mean에 수렴한다.
Central Limit Theorem
-
sample mean 은 (X의 분포와 상관없이) normal distribution을 따른다.
(X 는 IID)
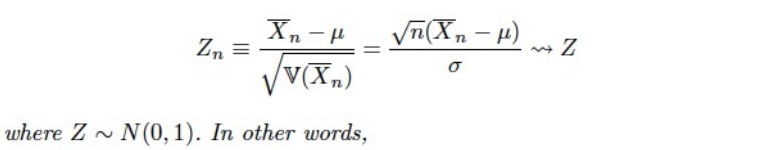
-
sample size가 커지면, sample variance는 모분산에 수렴한다.
이를 이용해, 아래와 같이 사용 가능하다.
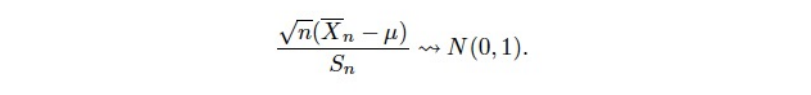
-
multuvariate CLT
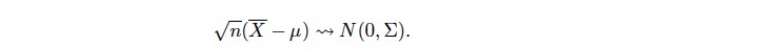
Delta Method
- 추정값 이 nomal distribution을 따르고, g가 미분가능한 함수일 때, 아래 성립
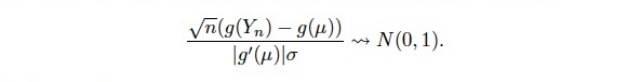
- =
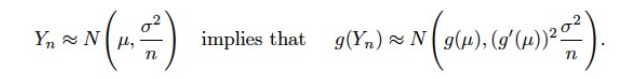
- Taylor Expansion 의 응용
