문제

다이아는 정말... 힘드네요

https://www.acmicpc.net/problem/10167
점과 가중치가 있을 때 x, y축과 평행한 직사각형으로 감싼 최대 2차원 연속합을 구하는 문제입니다.

풀이

연습 문제

연습문제로 [BOJ] 16992 / 연속합과 쿼리 문제를 먼저 풀이하는 것을 추천 드립니다.

연습 문제 풀이

연속합은 떨어지는 구간이 발생해서는 안됩니다. 따라서 기본적으로 연속합에 해당하는 구간이 왼쪽 끝, 오른쪽 끝에 닿는지 여부를 판단하는 것이 중요합니다. 이 여부에 따라 두 구간이 붙을 수 있는지 없는지에 대한 판단 기준이 됩니다.

결국 관리해야 되는 것은 4가지 입니다.

왼쪽 끝이 닿는 구간합(left)

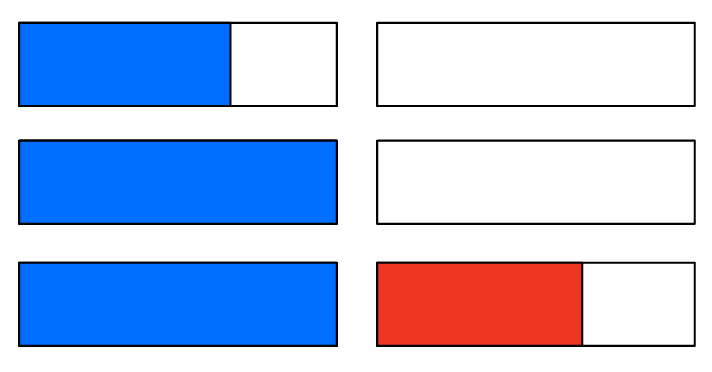
오른쪽 끝이 닿는 구간합(right)

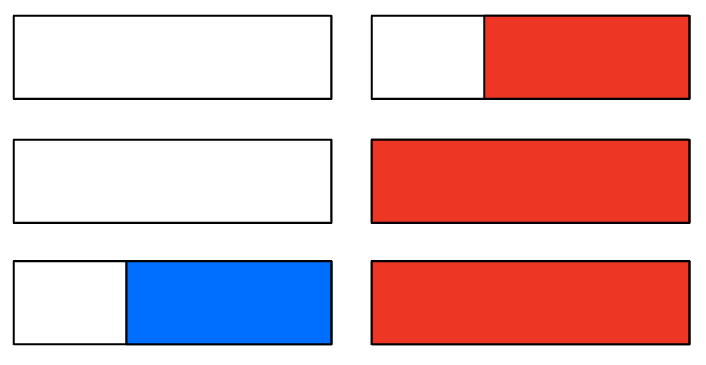
중간 부분에 걸친 구간합(mid)

전체 합(all)

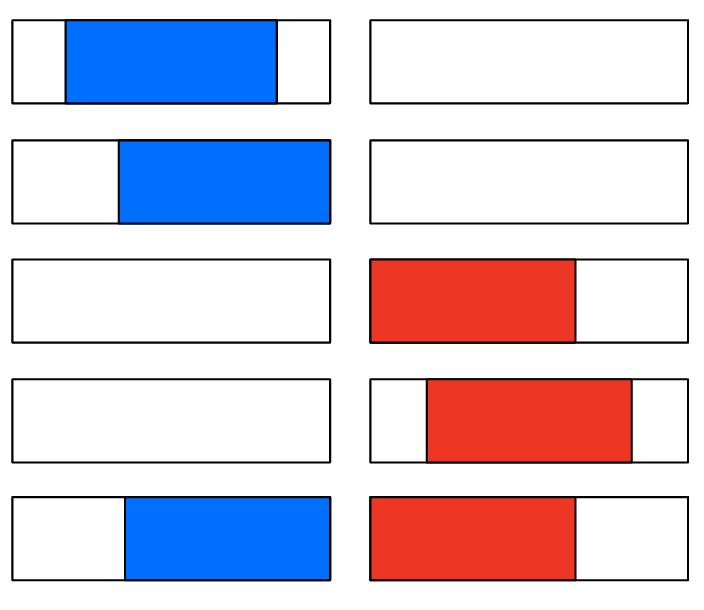
여기서 구간 내 최댓값은 사실상 모든 기준을 포함하는 mid 가 됩니다. 따라서 마지막에 get 할 때 mid 값을 가져오면 됩니다.

그리고 4개의 값을 가져와야 되므로 트리를 4개 만들어야 되는가 생각할 수 있는데, 4개나 따로 구현하기란 너무 귀찮은 일입니다. 이 4개를 하나로 통합하는 Node 를 만들어 관리하면 됩니다.

이제 남은 것은 두 구간합을 합치는 연산입니다. n1 노드와 n2 노드를 합치는 연산은 다음과 같습니다.

• left
  • 왼쪽 노드만 생각할 것인가 → n1.left
  • 오른쪽 노드도 고려할 것인가 → 왼쪽 전체 선택하고 오른쪽 노드의 left → n1.all + n2.left

  max(n1.left, n1.all + n2.left);

• right
  • 오른쪽 노드만 생각할 것인가 → n1.right
  • 왼쪽 노드도 고려할 것인가 → 오른쪽 전체 선택하고 왼쪽 노드의 right → n1.right + n2.all

  max(n2.right, n1.right + n2.all);

• mid
  • 왼쪽 노드만 생각할 것인가 → n1.mid
  • 오른쪽 노드만 생각할 것인가 → n2.mid
  • 둘을 이어 붙일 것인가 → 왼쪽 노드의 right + 오른쪽 노드의 left → n1.right + n2.left

  max(n1.mid, n2.mid, n1.right + n2.left);

• all
  • 둘 다 전체 선택한 거 더하면 됩니다.

  n1.all + n2.all

이 연산에 대한 항등원(세그먼트 트리 범위 밖일 경우 반환)도 생각해보면 다음과 같습니다.

• left, right, mid : max 연산의 항등원 → -INF
• all : + 연산의 항등원 → 0
  

참고로 정식 명칭은 MSP(Maximum Subarray Problem)라 하는데, 국내에서는 아래에 풀이할 금광 덕분에 금광세그라는 이름으로 더 많이 알려져 있습니다.

연습 문제 코드

import java.io.*;
import java.util.*;

public class Main {
    static class Node {
        int left, right, mid, all;

        Node() {
            this(-1_000_000_000);
            all = 0;
        }

        Node(int val) {
            left = right = mid = all = val;
        }
    }

    static int n, size;
    static int[] arr;
    static Node[] tree;

    static Node merge(Node n1, Node n2) {
        Node node = new Node();
        node.left = Math.max(n1.left, n1.all + n2.left);
        node.right = Math.max(n2.right, n1.right + n2.all);
        node.mid = Math.max(Math.max(n1.mid, n2.mid), n1.right + n2.left);
        node.all = n1.all + n2.all;
        return node;
    }

    static void init(int node, int s, int e) {
        if (s == e) {
            tree[node] = new Node(arr[s]);
            return;
        }
        int mid = (s + e) >> 1;
        init(node << 1, s, mid);
        init(node << 1 | 1, mid + 1, e);
        tree[node] = merge(tree[node << 1], tree[node << 1 | 1]);
    }

    static int query(int s, int e) {
        return get(1, 1, n, s, e).mid;
    }

    static Node get(int node, int s, int e, int ts, int te) {
        if (e < ts || te < s) return new Node();
        if (ts <= s && e <= te) return tree[node];
        int mid = (s + e) >> 1;
        Node l = get(node << 1, s, mid, ts, te);
        Node r = get(node << 1 | 1, mid + 1, e, ts, te);
        return merge(l, r);
    }

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
        StringTokenizer st;

        n = Integer.parseInt(br.readLine());
        size = 1 << ((int) Math.ceil(Math.log(n) / Math.log(2)) + 1);
        arr = new int[n + 1];
        tree = new Node[size];

        st = new StringTokenizer(br.readLine(), " ");
        for (int i = 1; i <= n; i++) {
            arr[i] = Integer.parseInt(st.nextToken());
        }

        init(1, 1, n);
        int m = Integer.parseInt(br.readLine());
        while (m-- > 0) {
            st = new StringTokenizer(br.readLine(), " ");
            int i = Integer.parseInt(st.nextToken());
            int j = Integer.parseInt(st.nextToken());
            sb.append(query(i, j)).append('\n');
        }

        System.out.print(sb);
        br.close();
    }
}

금광 풀이

지금까지 금광세그라는 것을 알아보았습니다. 하지만 이 세그를 알아도 풀이가 쉽지는 않습니다. 세그를 일단 생각하지 않고 접근 해보겠습니다.

처음 든 생각

[x1, x2] , [y1, y2] 범위의 점들을 선택해서 이 범위에 해당하는 점들의 합을 구합니다.

• [x1, x2] : O(N^2)
• [y1, y2] : O(N^2)
• 구간 내 점들의 합 : O(N^2)
• 전체 : O(N^6)

당연히 이렇게 풀면 TLE입니다. 여기서 힌트가 되는 것이 바로 서브테스크가 됩니다.

1. N ≤ 100 : O(N^6) 가능
2. N ≤ 500 : 조금 더 줄여야 됨
3. wi < 0 (1 개) : 연속합 중간에 끊기는 부분이 딱 하나 존재
4. y = 0 : 일직선 상에 존재하는 연속합의 최대, 위에서 설명한 금광세그 사용
5. 제약조건 없음 : 종합

점들 선택하는 과정

문제가 되는 부분은 바로 [x1, x2] , [y1, y2] 범위를 모두 본다는 것에 있습니다. 이중에서 하나만 보고 나머지는 뭔가 최적화하는 방법이 있을 것인지 생각해보는 것이 어떨까요?

마침 서브테스크 중에 y값이 같을 경우 어떻게 해결할 것인지 보는 것이 있습니다. [y1, y2] 에 대한 선택만 하도록 합니다 → O(N^2)

그러면 점들에 대한 순서 역시 필요하게 되고, 그 과정은 다음과 같습니다.

• y 기준으로 정렬
• y1을 고정하여 세그먼트 트리를 초기화
• 정점들을 하나씩 넣어서 세그먼트 트리를 갱신
  

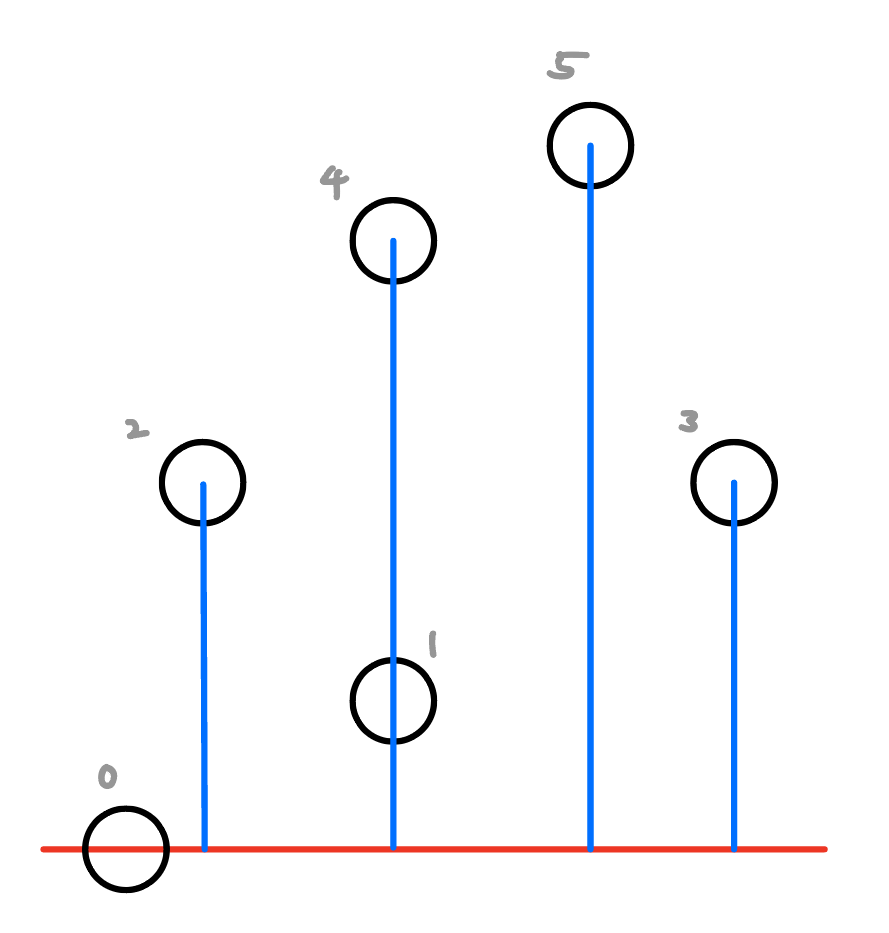
반례 잡기

이렇게 풀이하면 되는데, 반례 하나가 있습니다.

4
2 2 4
2 1 6
1 2 7
1 1 -1000

최대가 나올 수 있는 부분은 (1, 2) 와 (2, 1) 을 선택하면 됩니다. (답 : 11)

하지만 현재 풀이대로만 진행하면 17이 나옵니다. 문제의 원인은 다음과 같습니다.

• 정렬 순서 (1, 1) → (1, 2) → (2, 1) → (2, 2)
• (1, 1) 에서 4개의 점 삽입 시에는 문제 없음
• (1, 2) 에서 같은 높이에 있는 (1, 1)이 누락 → (1, 2), (2, 1), (2, 2) 만 포함된 범위가 계산됨 → error
  

즉, 같은 높이일 때는 해당하는 같은 높이의 모든 점을 다 삽입해주어야 됩니다.

다만, 조금 관점을 다르게 생각해서 x 좌표가 제일 작은 시점에서만 모두 넣어주고, 나머지는 모두 무시해보는 방법도 생각해볼 수 있습니다. 즉 중복은 무시해주면 됩니다.

for (int i = 0; i < n; i++) {
    // 같은 높이는 중복 처리 X
    if (i > 0 && point[i - 1].y == point[i].y) continue;
    init();
    for (int j = i; j < n; j++) {
        update((int) point[j].x, point[j].v);
        // 같은 높이는 모두 삽입된 후 처리
        if (j == n - 1 || point[j].y != point[j + 1].y) {
            res = Math.max(res, tree[1].mid);
        }
    }
}

코드

import java.io.*;
import java.util.*;

public class Main {
    static class Point implements Comparable<Point> {
        long x, y, v;
        int i;

        public Point(long x, long y, long v, int i) {
            this.x = x;
            this.y = y;
            this.v = v;
            this.i = i;
        }

        @Override
        public String toString() {
            return "[" + x + ", " + y + ", " + v + ", " + i + "]";
        }

        @Override
        public int compareTo(Point p) {
            return this.y == p.y ? Long.compare(this.x, p.x) : Long.compare(this.y, p.y);
        }
    }

    static class Pair {
        int idx;
        long val;

        public Pair(int idx, long val) {
            this.idx = idx;
            this.val = val;
        }

        @Override
        public String toString() {
            return "[" + idx + ", " + val + "]";
        }
    }

    static class Node {
        long left, right, mid, all;
    }

    static int n, m, size;
    static Node[] tree;
    static Point[] point;
    static Pair[] tmpX, tmpY;

    static void compression() {
        tmpX = new Pair[n];
        tmpY = new Pair[n];
        for (Point p : point) {
            tmpX[p.i] = new Pair(p.i, p.x);
            tmpY[p.i] = new Pair(p.i, p.y);
        }

        Arrays.sort(tmpX, (o1, o2) -> Long.compare(o1.val, o2.val));
        Arrays.sort(tmpY, (o1, o2) -> Long.compare(o1.val, o2.val));

        int ix = 0, iy = 0;
        for (int i = 0; i < n - 1; i++) {
            point[tmpX[i].idx].x = ix;
            if (tmpX[i].val != tmpX[i + 1].val) ix++;
        }
        point[tmpX[n - 1].idx].x = ix;

        for (int i = 0; i < n - 1; i++) {
            point[tmpY[i].idx].y = iy;
            if (tmpY[i].val != tmpY[i + 1].val) iy++;
        }
        point[tmpY[n - 1].idx].y = iy;

        Arrays.sort(point);
    }

    static void init() {
        for (int i = 0; i < size; i++) {
            tree[i].left = tree[i].right = tree[i].mid = (long) (-1e14);
            tree[i].all = 0;
        }
    }

    static Node merge(Node n1, Node n2) {
        Node node = new Node();
        node.left = Math.max(n1.left, n1.all + n2.left);
        node.right = Math.max(n2.right, n1.right + n2.all);
        node.mid = Math.max(Math.max(n1.mid, n2.mid), n1.right + n2.left);
        node.all = n1.all + n2.all;
        return node;
    }

    static void update(int idx, long val) {
        idx += m;
        tree[idx].all += val;
        tree[idx].left = tree[idx].right = tree[idx].mid = tree[idx].all;
        while ((idx >>= 1) > 0) {
            tree[idx] = merge(tree[idx << 1], tree[idx << 1 | 1]);
        }
    }

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        n = Integer.parseInt(br.readLine());
        m = 1 << (int) Math.ceil(Math.log(n) / Math.log(2));
        size = m << 1;
        tree = new Node[size];
        for (int i = 0; i < size; i++) tree[i] = new Node();
        point = new Point[n];
        for (int i = 0; i < n; i++) {
            st = new StringTokenizer(br.readLine(), " ");
            long x = Long.parseLong(st.nextToken());
            long y = Long.parseLong(st.nextToken());
            long v = Long.parseLong(st.nextToken());
            point[i] = new Point(x, y, v, i);
        }
        compression();

        long res = 0;
        for (int i = 0; i < n; i++) {
            if (i > 0 && point[i - 1].y == point[i].y) continue;
            init();
            for (int j = i; j < n; j++) {
                update((int) point[j].x, point[j].v);
                if (j == n - 1 || point[j].y != point[j + 1].y) {
                    res = Math.max(res, tree[1].mid);
                }
            }
        }

        System.out.println(res);
    }
}