[자료구조 & 알고리즘] Euler Tour Technique

개요

색깔 트리라는 문제를 풀어보며 다음과 같은 의문이 들었습니다.

만약 트리의 최대 깊이가 100이라서 단순 dfs로도 구현이 되는데, 만일 LCA 때처럼 10만이란 단위가 나온다면...?

여러가지 조건을 여기에 적용 가능하지만, 편의를 위해 다음과 같은 조건을 추가해보겠습니다.

대신 트리의 구조 자체는 변하지 않고 부모 노트 색 칠할 때 자식 노드도 모두 칠해지는 조건만 가져와서 적용해보자

Segment Tree with Lazy Propagation 을 적용하기에 딱 좋아보입니다. 그리고 마침 백준에 이에 해당하는 문제가 있습니다. 구조는 안바뀌는데, 뭔가 누적되는 것은 똑같아 보입니다. 하지만, O(depth) 로 처리 시에는 분명히 문제가 됩니다. 뭔가 O(1) 아니면 O(log N) 으로 접근하면 됩니다.

바로 세그먼트 트리로 관리 해주되, 해당되는 트리의 구간을 Lazy Propagation 을 활용해서 O(log N) 으로 진행하면 됩니다. 그런데 문제가 있습니다.

우리가 세그먼트 트리 만들 때는 분명히 완전 이진 트리여서 1차원 배열로 작성이 가능했습니다. 근데 저건 그런게 아니라 완전히 일반화된 트리입니다. 일반화된 트리를 저렇게 1차원 배열 형식으로 가능…은 할까요…?

네 가능합니다. 대신 특별한 기술이 들어갑니다. 바로 Euler Tour Technique(ETT) 입니다.

Euler Tour Technique(ETT)

ETT는 트리를 1차원 배열로 변환하는 기법으로, 트리에서 특정 노드의 서브트리를 연속된 구간으로 변환하여 세그먼트 트리와 같은 자료구조를 활용할 수 있도록 합니다.

트리는 일반적으로 계층적 구조를 가지고 있어서 1차원 배열을 기반으로 동작하는 세그먼트 트리나 펜윅 트리를 직접 적용하기 어렵습니다.

하지만 dfs를 수행하며 트리를 펼쳐서 1차원 배열로 표현하면 O(log N)의 시간 복잡도로 서브트리 연산이 가능해집니다.

ETT 과정

ETT의 과정은 다음과 같습니다.

1. dfs를 수행하며 정점을 방문하는 순서를 기록합니다.
2. 각 노드의 "들어온 시간 (In-Time)"과 "나가는 시간 (Out-Time)"을 저장합니다.
3. In-Time과 Out-Time을 이용해 서브트리를 하나의 연속된 구간으로 표현합니다.

뭔가 복잡해 보이지만, 사실은 단순한 개념입니다. 트리를 dfs로 순회하며 각 노드가 언제 탐색을 시작하고 끝나는지만 기록하면 됩니다.

이 방식은 dfs numbering 이라고도 부릅니다. 코드로도 아주 간단합니다.

int cnt = 0;
void dfs(int node) {
	in[node] = ++cnt; // 시작 번호 마킹
	// 탐색 부분
	out[node] = cnt;
}

아래는 트리에 대해서 dfs numbering을 진행한 결과입니다.

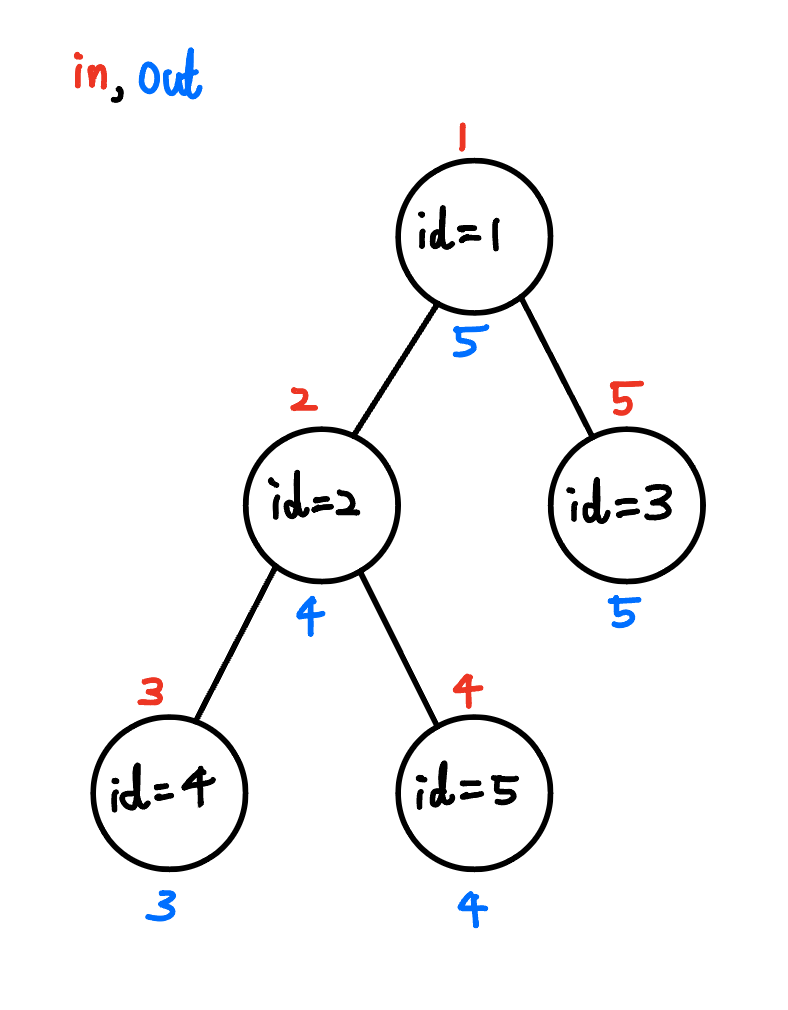
표로 나타내면 다음과 같습니다.

구분	1번 노드	2번 노드	3번 노드	4번 노드	5번 노드
in	1	2	5	3	4
out	5	4	5	3	4
idx(id)	1	2	3	4	5

이렇게 만들면 트리를 1차원 배열로 만들 준비가 끝났습니다. 적용은 다음과 같이 하면 됩니다.

idx(in/out)	ㅤㅤ0ㅤㅤ	ㅤㅤ1ㅤㅤ	ㅤㅤ2ㅤㅤ	ㅤㅤ3ㅤㅤ	ㅤㅤ4ㅤㅤ	ㅤㅤ5ㅤㅤ
1번 루트 서브 트리		in[1]				out[1]
2번 루트 서브 트리			in[2]		out[2]
3번 루트 서브 트리						in[3] out[3]
4번 루트 서브 트리				in[4] out[4]
5번 루트 서브 트리					in[5] out[5]

이렇게 구간으로 관리할 수 있습니다. 이제는 Lazy Propagation 활용해서 구간 관리하면 됩니다.

[BOJ] 16404 / 주식회사 승범이네

위 과정으로 얻은 서브트리 구간을 Segment tree with Lazy Propagation 을 통해 구간 갱신, 현재 노드 값은 시작 값을 가져와서 그대로 Segment tree에서 가져오면 됩니다.

#include <iostream>
#include <vector>

using namespace std;
typedef long long ll;

const int MAX = 100'001;

int n;
int num = 0;
int depth[MAX], s[MAX], e[MAX];
ll lazy[4 * MAX], tree[4 * MAX];
vector<int> g[MAX];

void dfs(int cur, int d) {
	depth[cur] = d;
	s[cur] = ++num;
	for (int nxt : g[cur]) {
		if (depth[nxt] == 0) {
			dfs(nxt, d + 1);
		}
	}
	e[cur] = num;
}

void updateLazy(int node, int s, int e) {
	if (lazy[node] == 0) return;
	tree[node] += (e - s + 1) * lazy[node];
	if (s != e) {
		lazy[node << 1] += lazy[node];
		lazy[node << 1 | 1] += lazy[node];
	}
	lazy[node] = 0;
}

void updateTree(int node, int s, int e, int ts, int te, int val) {
	updateLazy(node, s, e);
	if (te < s || e < ts) return;
	if (ts <= s && e <= te) {
		tree[node] += val;
		if (s != e) {
			lazy[node << 1] += val;
			lazy[node << 1 | 1] += val;
		}
		return;
	}

	int m = (s + e) >> 1;
	updateTree(node << 1, s, m, ts, te, val);
	updateTree(node << 1 | 1, m + 1, e, ts, te, val);
	tree[node] = tree[node << 1] + tree[node << 1 | 1];
}

ll get(int node, int s, int e, int ts, int te) {
	updateLazy(node, s, e);
	if (te < s || e < ts) return 0;
	if (ts <= s && e <= te) return tree[node];

	int m = (s + e) >> 1;
	return get(node << 1, s, m, ts, te) + get(node << 1 | 1, m + 1, e, ts, te);
}

void update(int i, int w) {
	updateTree(1, 1, n, s[i], e[i], w);
}

ll balance(int i) {
	return get(1, 1, n, s[i], s[i]);
}

int main() {
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	int m, p;
	cin >> n >> m;
	for (int i = 1; i <= n; ++i) {
		cin >> p;
		if (p == -1) continue;
		g[p].emplace_back(i);
	}

	dfs(1, 1);
	fill(lazy, lazy + (4 * n + 1), 0);
	fill(tree, tree + (4 * n + 1), 0);

	int q, i, w;
	while (m--) {
		cin >> q;
		if (q == 1) {
			cin >> i >> w;
			update(i, w);
		}
		else {
			cin >> i;
			cout << balance(i) << '\n';
		}
	}

	return 0;
}