[Math] Numerical Integration

여러 함수들의 적분은 간단한 꼴로 나타낼 수 없다. 예를 들어, $\sin{x^2}$나 $\frac{1}{\ln{x}}$와 같은 함수는 그 적분을 간단히 나타낼 수 없다. 이와 같이 적분해야 하는 함수의 적분을 찾기 어려울 때, 주어진 부분구간에서 함수 $f$와 비슷한 함수로 대체한 다음 이 함수의 적분값을 더하여 함수 $f$의 적분값을 구하는 방법을 수치적분(numerical integration)이라고 한다. 수치적분은 대부분의 경우 매우 많은 양의 계산을 필요로 한다. 본 보고서에서는 몇 가지의 대표적인 수치적분 방법을 알아보고, 이를 python을 이용하여 구현한다.

구분구적법

가장 간단한 수치적분 방법 중 하나는 구분구적법이다. 함수의 그래프를 매우
작은 직사각형으로 잘게 나누어 그 사각형들의 넓이의 합을 이용하여
정적분을 구하는 방법을 구분구적법이라고 한다.

구현

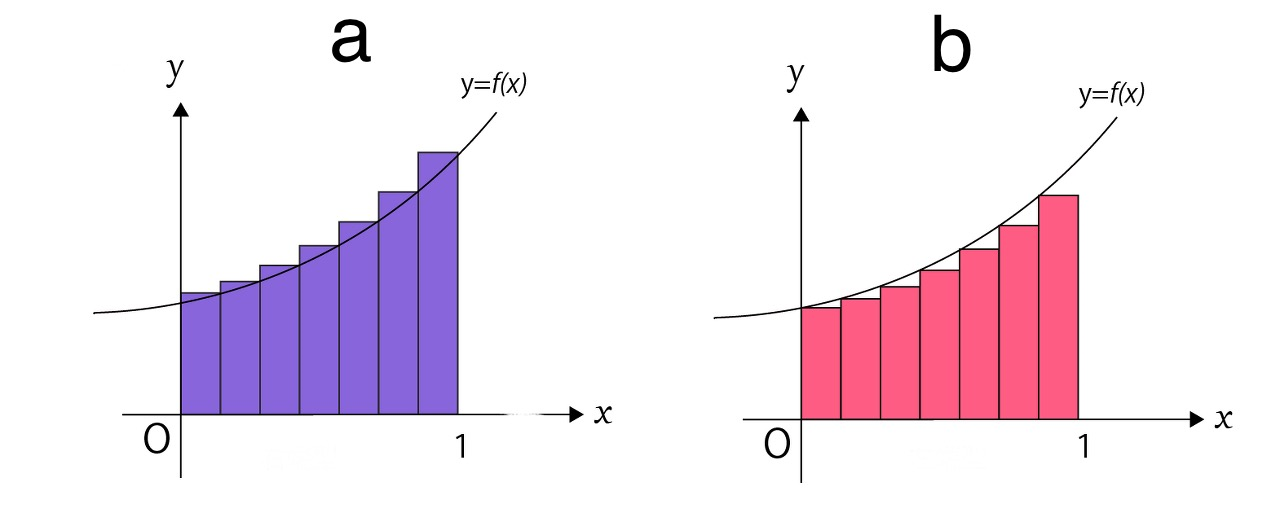
rectangle1과 rectangle2는 각각 아래 그림에서의 a와 b를 코드로 구현한 함수이다.

def rectangle(n, a, b):
    S = 0.0
    h = (b - a) / n

    for i in range(1, n + 1):
        S += f(a + (i - 1) * h) * h

    return S

def rectangle2(n, a, b):
    S = 0.0
    h = (b - a) / n

    for i in range(1, n + 1):
        S += f(a + i * h) * h

    return S

사다리꼴 공식

사다리꼴 공식은 우리가 앞서 학습한 구분구적법에서 직사각형 대신
사다리꼴을 적용한 방법이다. 함수 $f$를 구간 $[a,b]$에서 적분하는 경우를
생각하자. 구간 $[a,b]$를 $n$등분한 분할을 생각하자.
$a= x_0 < X_1 < x_2 < \cdot < x_{n-1} < x_n = b$에서, 부분구간의 길이는
$\Delta x = \frac{b-a}{n}$이다. $y_i = f(x_i )$일 때, $i$번째 구간의
사다리꼴 넓이는
$\Delta x \left( \frac{Y_{i-1} + y_i}{2} \right)= \frac{\Delta x}{2}\left( y_{i-1}+y_i \right)$이다.
$\Delta x$를 높이로 삼는다면 수직으로 놓인 두 변의 평균과 곱한 값이
넓이이다. 곡선 아래 넓이는 다음 식과 같이 모든 사다리꼴의 넓이를 더하여 근사값을 구한다.

따라서 다음과 같이 적분의 근사값을 구할 수 있다.

구현

앞에서 구현한 구분구적법과 비슷한 방법을 이용하여 사다리꼴 공식을 python을 이용하여 구현할 수 있었다.

def trapezoidal(n, a, b):
    S = 0.0
    h = (b - a) / n

    for i in range(1, n):
        S += f(a + i * h)

    S = (f(a) + 2 * S + f(b)) * h / 2.0
    return S

심프슨 1/3 공식

세 점을 지나는 포물선을 구하여 적분한 값을 더하여 근사값을 구하는 것을 심프슨 공식이라고 한다. 세 점 $(x_{0}, y_{0}),(x_{1}, y_{1}), (x_{2}, y_{2})$를 지나는 포물선을 생각하자. $x_0 = -h, x_1 = 0, x_2 = h$이라고 하자. 이때 $h=\Delta x = \frac{b-a}{n}$이 된다. 포물선의 방정식을

라고 하면 이 포물선의 아래 면적은

세 점 $(-h, y_{0}),(0, y_{1}), (h, y_{2})$가 포물선 위에
있으므로

따라서 위에서 구한 넓이는

마찬가지로 $(x_{2}, y_{2}),(x_{3}, y_{3}), (x_{4}, y_{4})$를 지나는 포물선 아래 넓이는

따라서 다음 식과 같이 근사값을 구할 수 있다.

구현

짝수항을 다 더하고, 홀수항을 모두 더하여 그 둘의 합을 구하는 방법으로 간단하게 심프슨 1/3공식을 구현할 수 있었다.

def simpson(n, a, b):
    h = (b - a) / (2 * n)
    S1 = 0.0
    S2 = f(a + h)

    for i in range(2, 2 * n, 2):
        S1 += f(a + i * h)
        S2 += f(a + (i + 1) * h)