
병합 정렬Merge Sort(합병이라고도 합니다)에 대해 다뤄보겠습니다!
병합 정렬
대표적인 분할 정복Divide-and-conquer 알고리즘입니다.
분할 정복
큰 문제를 작은 문제로 나눠 해결해가는 방식
정렬 알고리즘 중에 빠른 알고리즘에 속하며, 퀵 정렬Quick Sort보다 빠를 때도 있고 Stable합니다. 하지만 퀵 정렬Quick Sort가 더 많이 쓰이는데요, 이건 아래에 설명할게요.
전개 방식은 아래와 같아요.
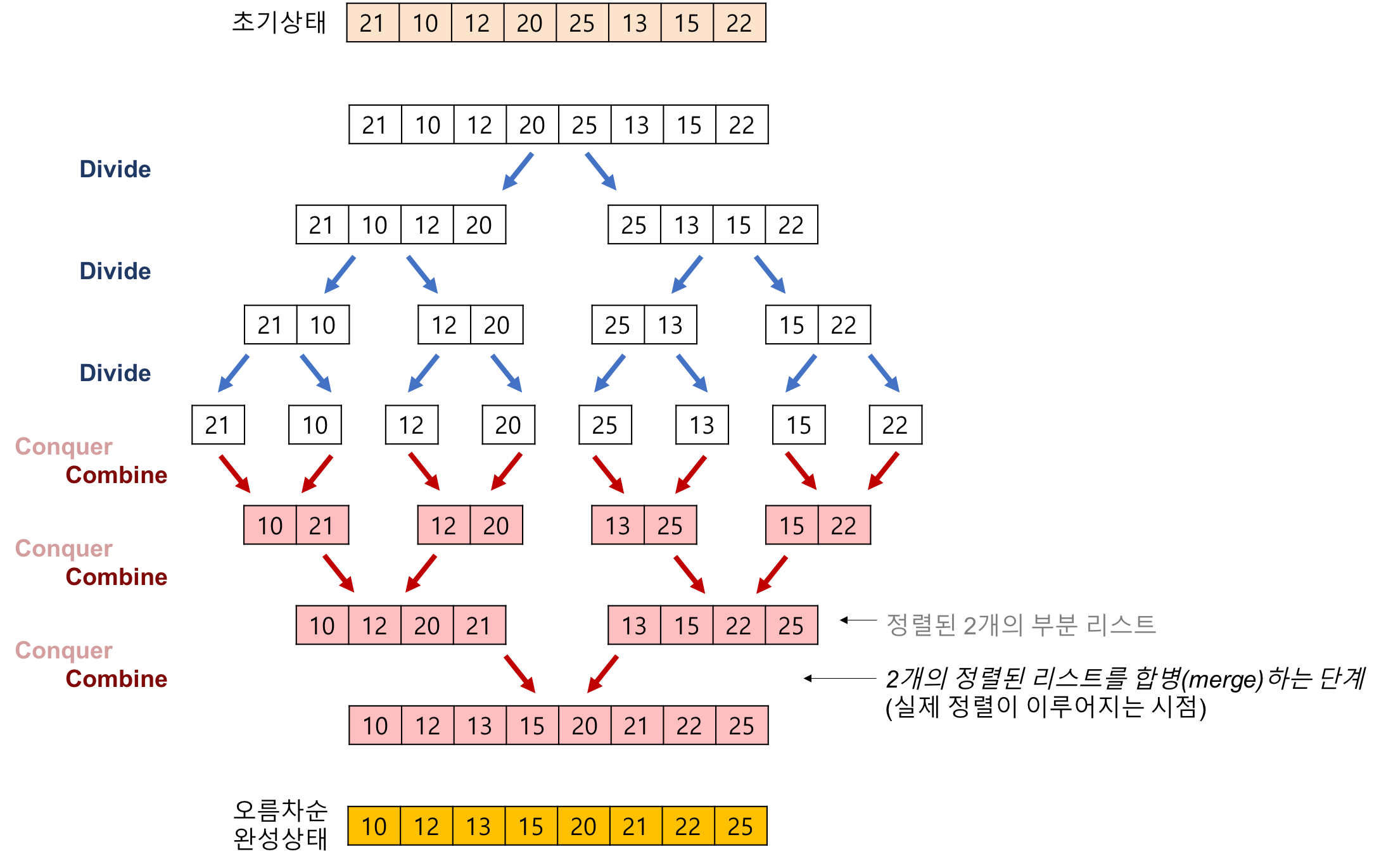
- 배열을 반으로 나눌 수 없을 때까지 계속 쪼갭니다.
- 이후 쪼갠 배열을 '새로운 배열'에 나눠서 정렬합니다. ->
Merge- 정렬이 완료되면 쪼갠 영역을 다시 붙여
Merge를 수행합니다.
특징
병합 정렬Merge Sort는 최선, 평균, 최악이 모두 으로 최악의 시간복잡도가 인 퀵 정렬보다 효율적이고, Stable합니다.
하지만, merge를 하는 과정에서 추가로 배열을 생성해야하기 때문에 In-place한 정렬은 아니에요. 그래서 퀵 정렬이 더 많이 사용됩니다.
소스
#include <vector>
template<typename T>
class MergeSort
{
public:
static void sort(vector<T>& arr)
{
mergeSort(arr, 0, arr.size() - 1);
}
private:
static void mergeSort(vector<T>& arr, int start, int end)
{
if(start >= end)
return;
int mid = (start + end) >> 1;
mergeSort(arr, start, mid);
mergeSort(arr, mid + 1, end);
merge(arr, start, end);
}
static void merge(vector<T>& arr, int start, int end)
{
if(start >= end)
return;
int mid = (start + end) >> 1;
vector<T> lArr(arr.begin() + start, arr.begin() + mid + 1);
vector<T> rArr(arr.begin() + mid + 1, arr.begin() + end + 1);
int ll = lArr.size(), rl = rArr.size();
int i = 0, j = 0, k = start;
while(i < ll && j < rl)
{
if(lArr[i] <= rArr[j]) arr[k++] = lArr[i++];
else arr[k++] = rArr[j++];
}
while(i < ll) arr[k++] = lArr[i++];
while(j < rl) arr[k++] = rArr[j++];
}
};