문제

Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of the line i is at (i, ai) and (i, 0). Find two lines, which, together with the x-axis forms a container, such that the container contains the most water.

Notice that you may not slant the container.

제한사항

• n == height.length
• 2 $\leq$ n $\leq$ $10^5$
• 0 $\leq$ height[i] $\leq$ $10^4$

접근1

전형적인 투 포인터Two Pointer 알고리즘 문제입니다.

기둥이 주어졌을 경우, 가장 많은 물을 담을 수 있도록 기둥을 설치하는 문제입니다. 참고로 기울이는 경우는 안 따진다네요. 농담도 참 잘해요 하하하

투 포인터는 기본적으로 $O(n^{2})$의 시간 복잡도를 가져요. 그래서 최대 $10^{5}$개의 기둥을 가진 경우, 전부 처리하게 되면 시간 초과가 발생하게 됩니다. 우선 생각나는데로 Brute-force 처리를 했지만, 역시나 시간 초과가 발생했습니다.

답안1

class Solution {
    public int maxArea(int[] height) {
        if(height.length <= 2){
            return (height[0] < height[1]) ? height[0] : height[1];
        }

        int answer = 0;

        for(int nLeft = 0; nLeft < height.length - 1; ++nLeft){
            int nRight = height.length - 1;
            while(nLeft < nRight){
                int nOffset = (height[nLeft] < height[nRight]) ? height[nLeft] : height[nRight];
                int nValue = nOffset * (nRight - nLeft);
                if(answer < nValue)
                    answer = nValue;

                --nRight;
            }
        }

        return answer;
    }
}

접근2

시간 초과가 발생했으니 다른 방식이 필요했습니다. 불필요한 처리를 최대한 배제하고 그 중 최대의 값을 구하면 되는 문제였어요.

생각하다가, 좌우 기둥을 기준으로 좌측이 우측보다 작으면 더 큰 기둥을 찾기 위해 좌측을 이동, 반대의 경우 반대를 이동시키는 방식을 생각했어요.

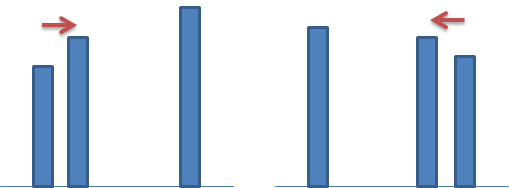
그 다음에 생각한 문제가 좌/우측의 기둥이 서로 같으면 어떻게 하는가였어요.

고민한 결과, 어떤 기둥을 이동한들 결국엔 최댓값을 비교해서 서로 기둥을 이동하기 때문에 괜찮다는 결과를 냈고, 정답을 제출하였습니다.

답안2

class Solution {
    public int maxArea(int[] height) {
        if(height.length <= 2){
            return (height[0] < height[1]) ? height[0] : height[1];
        }

        int answer = 0;

        int nLeft = 0, nRight = height.length - 1;
        while(nLeft < nRight){
            final int lValue = height[nLeft];
            final int rValue = height[nRight];

            int nOffset = (lValue < rValue) ? lValue : rValue;
            int nValue =  nOffset * (nRight - nLeft);
            if(answer < nValue)
                answer = nValue;

            if(lValue < rValue)
                ++nLeft;
            else
                --nRight;
        }


        return answer;
    }
}