문제

Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.

제한사항

• ${1}\leq{n}\leq{8}$

접근

생성 가능한 괄호 셋의 수가 주어졌을 때 만들 수 있는 모든 경우의 문자열을 반환하는 문제였습니다.

답안의 양식을 봤었을 때 이 문제는 DFS 방식으로 풀어야 순서도 맞출 수 있는 결과를 반환한다는 사실을 발견했어요.

문제는 부적절한 괄호 셋을 어떻게 속아내는 것인가 였어요. 그리고 발견한 것은,

1. 열린 괄호는 n의 수까지 무조건 추가가 가능합니다.
2. 닫힌 괄호는 추가된 열린 괄호의 개수보다 적게 있을 때만 추가합니다.

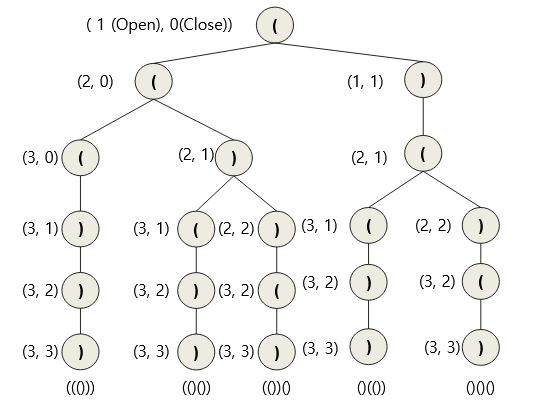
닫힌 괄호가 열린 괄호보다 많다면 부적절한 셋이 된다는 사실을 알았고, 이를 기반으로 문제를 푸니 해결되었습니다.

처음에 풀었을 때 String 타입에 추가하는 방식으로 진행하니 속도면에서 다소 느려, 답안을 보니 다른 풀이는 StringBuilder를 풀어서 해결했더라고요. 이걸 StringBuiler로 바꾸니 1등 속도 풀이와 동일한 속도가 나왔습니다. StringBuilder의 중요성을 다시금 깨닫습니다.

답안

import java.util.ArrayList;
import java.util.List;

public class Solution {
    public void generateRecursively(int n, int openCnt, int closeCnt, StringBuilder parentheses, List<String> ret){
        if(openCnt == n && closeCnt == n){
            ret.add(parentheses.toString());
            return;
        }

        if(openCnt < n){
            parentheses.append("(");
            generateRecursively(n, openCnt + 1, closeCnt, parentheses, ret);
            parentheses.setLength(parentheses.length() - 1);
        }

        if(closeCnt < n && openCnt > closeCnt){
            parentheses.append(")");
            generateRecursively(n, openCnt, closeCnt + 1, parentheses, ret);
            parentheses.setLength(parentheses.length() - 1);
        }
    }
    public List<String> generateParenthesis(int n) {
        List<String> ret = new ArrayList<>();
        if(n == 1){
            ret.add("()");
            return ret;
        }

        generateRecursively(n, 0, 0, new StringBuilder(), ret);

        return ret;
    }
}