프로그래밍 입문 시 보통 처음으로 접하게 되는 정렬 거품 정렬Bubble Sort에 대해 다뤄보겠습니다.

거품 정렬

서로 인접한 원소들끼리 비교해서 현재 인덱스 기준, 다음 인덱스의 원소가 크면 위치를 바꿔주는 방식으로 진행되요.

1. i번째 인덱스부터 시작하여 다음 인덱스i+1의 원소가 현재 i번째보다 크면 바꿔줍니다. (${0}\leq{i}<{n - 1}$)
   1-1. 이 때 마지막인덱스에선 해당 위치에 적합한 그 시점에 가장 큰 원소가 배치됩니다.
2. 따라서, 이후 ${i+1}\leq{i}<{n - i}$ 범위를 반복하면 정렬이 완료됩니다.

그림

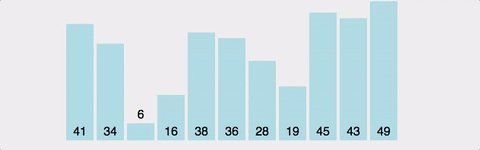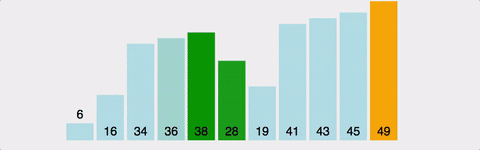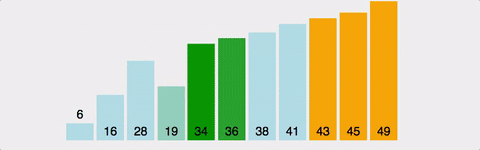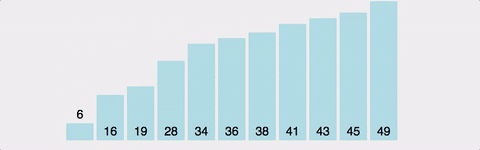
시간복잡도

(n-1) + (n-2) + $\dots$ + 1 = $\frac{n(n+1)}{2}$가 되므로 시간복잡도는 $O({n}^{2})$이 됩니다. 정렬 여부에 관계 없이 동일한 로직을 수행하므로 최선, 평균, 최악 모두 $O({n}^{2})$이에요.

소스

template<typename T>
class BubbleSort
{
public:
	static void sort(vector<T>& arr)
	{
		if(arr.size() <= 1)	return;

		for(int i = 0; i < arr.size(); ++i)
		{
			for(int j = 1; j < arr.size() - i; ++j)
			{
				if(arr[j] < arr[j - 1])
					swap(arr[j], arr[j - 1]);
			}
		}
	}
};