자료구조의 기본이 되는 배열Array와 연결 리스트Linked List에 대해 다뤄보아요.

배열(Array)

가장 기본적인 자료구조입니다.

논리적 저장 순서와 물리적 저장 순서가 일치합니다. 따라서, 인덱스index를 통해 해당 원소element에 접근이 가능합니다.

아랫 부분이 인덱스index 값입니다. 즉, 인덱스는 0부터 시작하며 크기가 n일 경우 접근할 수 있는 인덱스의 최대 값은 n - 1입니다.

인덱스를 통해 찾을 수 있다는 것은 찾고자 하는 위치만 알고 있으면 O(1)의 속도로 접근이 가능하며, 이는 임의 접근Random Access가 가능하다는 것을 의미합니다.

추가, 삭제가 쉽지 않다

마냥 좋아 보이지만, 배열은 한번 생성된 후 원소element 추가/삭제를 원할 경우 작업을 따로 해줘야 하는 문제가 있어요.

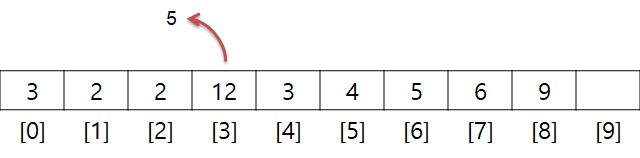
삭제를 예로 들면, 3번째 원소를 지우려고 하면 삭제한 인덱스보다 큰 원소들을 우측으로 shift를 해주어야 합니다. 거기다 배열 개수도 이에 맞춰 주고 싶으면 배열을 기존 배열보다 1 작은 크기로 생성을 하고 복제를 해줘야하죠. 이 경우 최악의 경우 모든 원소들을 shift 해줘야 하기 때문에 O(n)이 발생합니다. 삽입도 마찬가지죠.

연결 리스트(Linked List)

배열Array과 달리 추가/삭제가 용이한 자료구조입니다. 각 원소들은 자기 자신 다음 원소가 어떤 것인지만 기억하고 있어요. 이전 것을 기억할 수 없습니다. 이걸 단일 연결리스트`Single Linked List라고 합니다. 이를 보완한 양방향 연결 리스트Circular Linked List도 존재하지만 추후에 다루도록 할게요.

연결 리스트는 추가/삭제가 용이합니다. 배열과 달리 원소와 다음 원소 정보를 기억하는 next를 가지고 있는데 이를 노드Node라고 합니다.

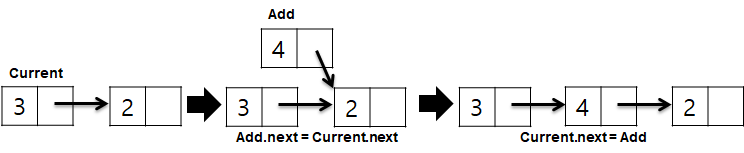
해당 위치에 추가를 원할 경우 위치에 있는 노드Current의 next를 추가하려는 노드Add의 next가 참조하고 노드Current의 next가 Add를 참조하면 됩니다.

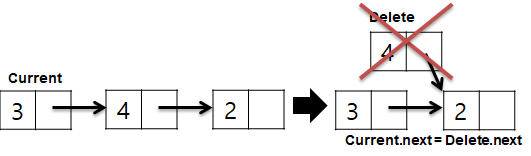
삭제의 경우 Current가 삭제하려는 노드Delete의 next를 참조하면 됩니다. 결과적으로 추가/삭제가 O(1)이 됩니다.

리스트도 마냥 완벽한 것은 아니다.

연결 리스트의 단점은 배열과 달리 임의 접근Random Access가 아니라 순차적 접근입니다. 즉, 특정 위치의 원소를 찾는데 필요한 시간은 O(n)이에요.

이는 배열Array와 달리 논리적 저장 순서와 물리적 저장 순서가 일치하지 않기 때문입니다. 이 때문에 찾아서 추가/삭제를 수행하기 위해 결국 O(n)의 수행 시간을 거칩니다.

그렇다고 마냥 의미 없는 자료구조는 아닙니다. 연결 리스트는 추후 트리Tree 등 유용한 알고리즘의 근간이 되기 때문에 기본적으로 학습해야할 자료구조 중 하나입니다.

오늘은 여기까지 다루겠습니다.