이진 탐색 트리

원리 : Parent Node보다 값이 작으면 왼쪽으로 값이 크거나 같으면 오른쪽으로 노드를 생성한다

노드 생성

class Node:
  def __init__(self,value):
     self.value=value
     self.left= None
     self.right=None

링크드 리스트를 이용해 연결

이진 탐색 트리 삽입

    def insert(self,value): #이진트리 탐색 삽입
        self.current_node = self.head
        while True:
            if value < self.current_node.value:
                if self.current_node.left!=None:
                    self.current_node = self.current_node.left
                else:
                    self.current_node.left= Node(value)
                    break
            else:
                if self.current_node.right != None:
                    self.current_node= self.current_node.right
                else:
                    self.current_node.right=Node(value)
                    break      

현재 노드를 루트 노드로 지정을 해서 삽입할 위치를 찾는다
현재노드의 값보다 작을 때는 왼쪽으로 이동하고
현재노드의 값보다 클 때는 오른쪽으로 이동시킨다
중요한 포인트는 값을 비교할 떄 공간이다
예를 들어서 현재노드의 값보다 작으면 왼쪽으로 이동해야 하지만 현재노드의 왼쪽에 노드가 존재하지 않으면 그 공간에 삽입을 해주면되고 노드가 존재하면 현재노드의왼쪽으로 이동하면 된다.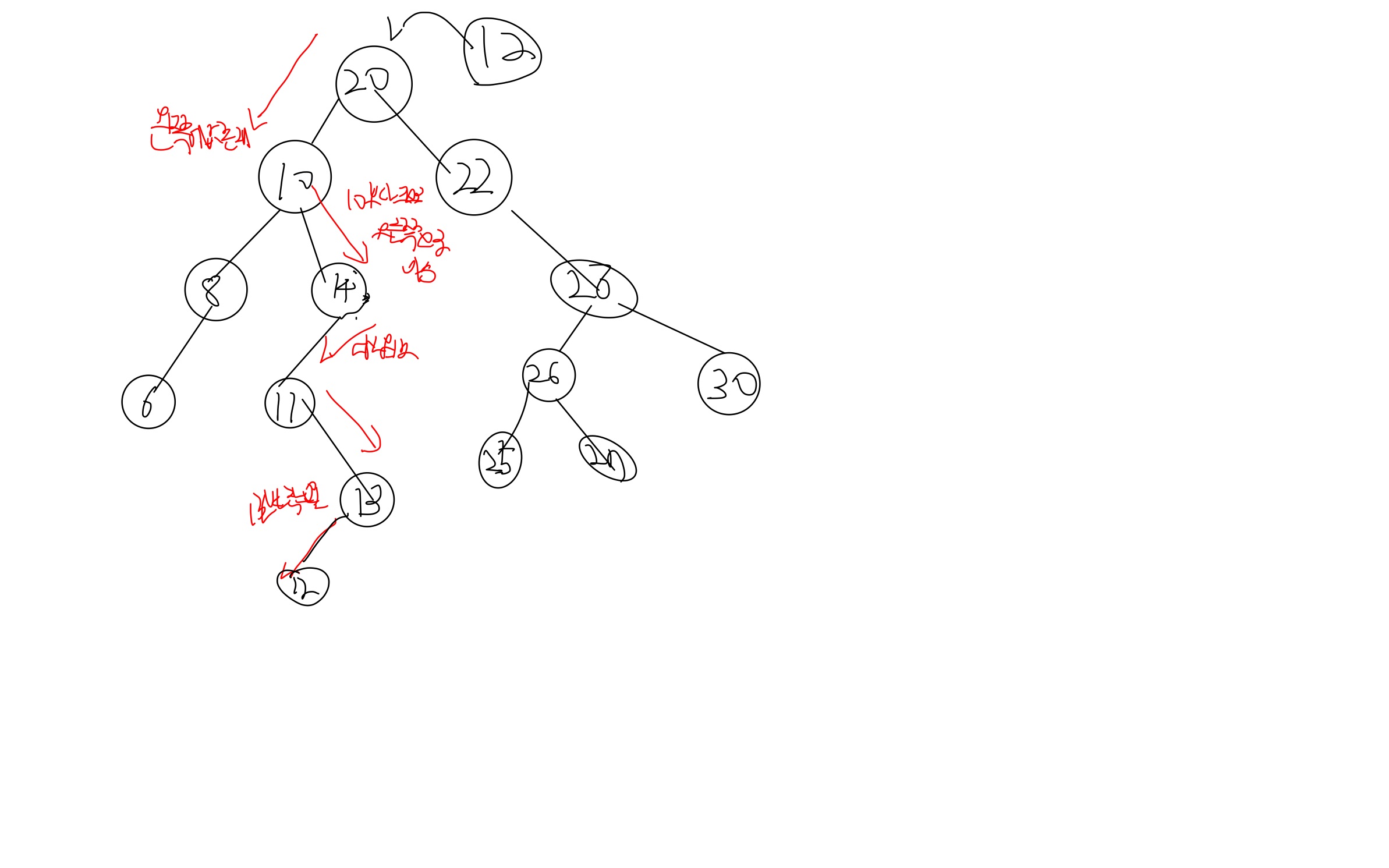

이진 검색 트리 탐색

어떠한 값을 받으면 그 값이 트리에 존재하는지 안하는지 판단

def search(self,value):
        self.current_node= self.head
        while self.current_node:
            if self.current_node.value==value:
                return print(True)
            elif value < self.current_node.value:
                self.current_node=self.current_node.left
            else :
                self.current_node=self.current_node.right
        return print(False)

while문에 현재 노드의 값이 있을때만 동작하게 해서
현재 노드의 값이 입력값보다 클 떄는 left로 이동
작을 때는 right로 이동
같을 때는 True를 리턴시킨다

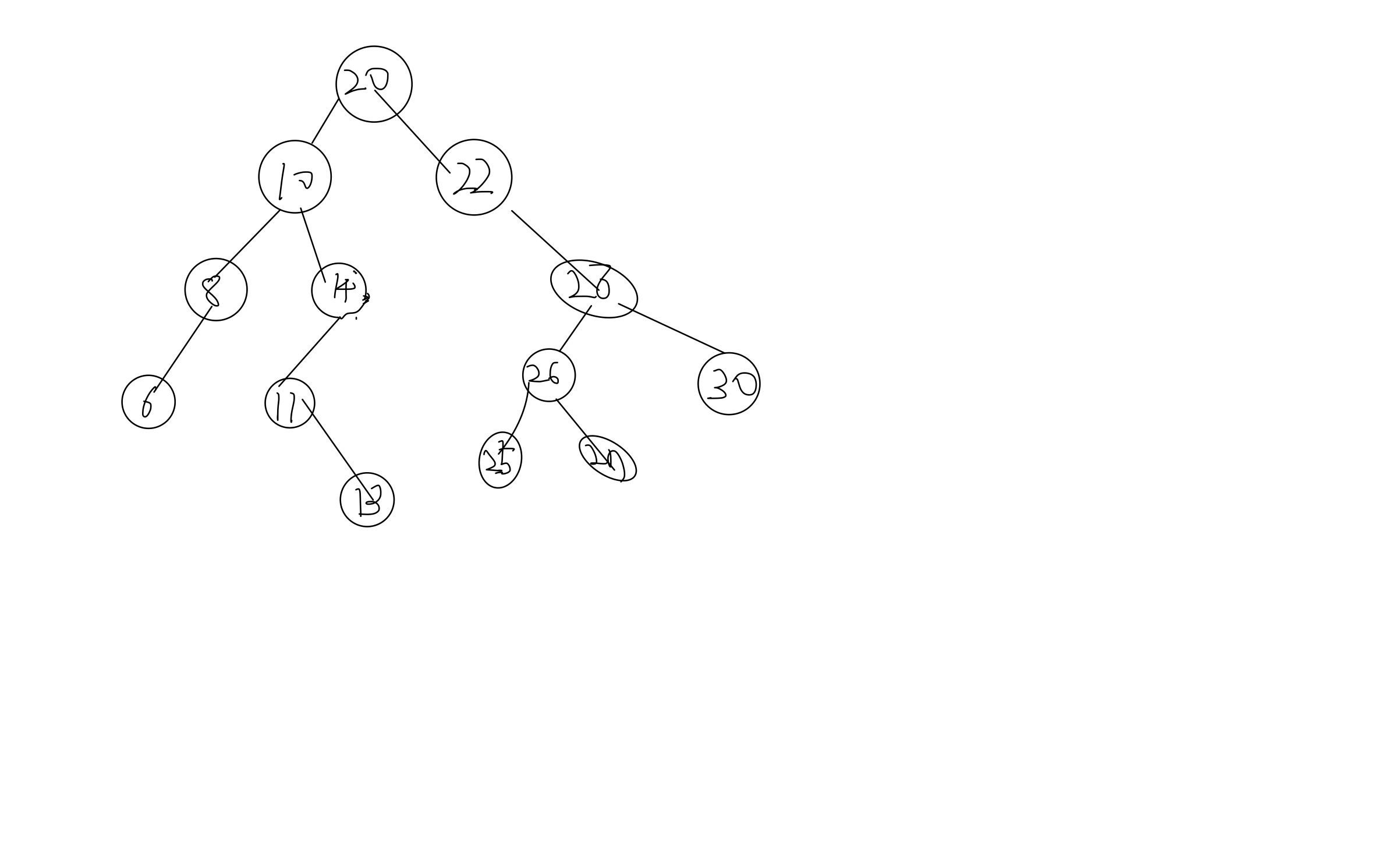
이진 검색 트리의 삭제

삭제가 경우의 수가 너무나도 많다
일단 탐색을 통하여 입력값에 대응되는 노드의 위치를 탐색한다

        searched = False # 이 트리에 FAlse면 존재X
        self.current_node=self.head
        self.parent= self.head # 삭제할 노드 위에 있는 parent node
        while self.current_node:
            if self.current_node.value == value:
                searched = True
                break
            elif value < self.current_node.value:
                self.parent= self.current_node
                self.current_node= self.current_node.left
            else:
                self.parent = self.current_node
                self.current_node = self.current_node.right
        if searched == False:
            return print(False)

탐색할 시엔

삭제할 노드의 위치를 찾은 다음 삭제를 진행하자

1. 삭제할 노드가 leaf Node일 경우
   leaf Node란 자손이 없는 경우이다
   이 경우에는 자손이 없기 때문에 까다로운 것이 없고
   삭제할 노드의 바로 위 부모 노드와의 연결을 끊어버리면 된다

  if self.current_node.left == None and self.current_node.right == None:
            if value < self.parent.value:
                self.parent.left = None
            else:
                self.parent.right = None
            del self.current_node

2. 삭제할 노드가 자식 노드를 한 개 가질 때
   삭제할 노드의 자식노드가 삭제할 노드의 왼쪽에 있는지 오른쪽에 있는지 찾은 후에 삭제할 노드를 삭제하고 삭제할 노드의 자식노드를 부모노드에 연결해주면된다

   if self.current_node.left != None and self.current_node.right == None:
            if value < self.parent.value:
                self.parent.left=self.current_node.left
            else:
                self.parent.right=self.current_node.left
        elif self.current_node.left == None and self.current_node.right != None:
            if value < self.parent.value:
                self.parent.left= self.current_node.right
            else :
                self.parent.right=self.current_node.right

3.마지막으로 자식노드를 양쪽 다 가질 때
이때가 경우의 수가 조금 복잡하다
일단 크게 두갈래로 나누어 지는데

1. 삭제노드가 부모노드 왼쪽에 있을 떄
2. 삭제노드가 부모노드 오른쪽에 있을 때

1번의 경우
삭제노드의 오른쪽 노드에서 제일 값이 낮은 녀석을 찾으면 된다
그 말은 삭제노드의 오른쪽 노드에서 계속 왼쪽으로 이동하면 되는데
여기서 또 경우의 수가 발생한다

1-1. 삭제 노드 오른쪽 노드에서 맨 왼쪽 노드를 찾을 떄 그 노드에게 자손이 있을 때(즉 그 노드에서 오른쪽 노드가 있을때ㅣ)
1-2. 삭제 노드 오른쪽 노드에서 맨 왼쪽 노드를 찾을 때 그 노드에게 자손이 없을 때

즉 17번 노드의 존재 유무에 따라 분기해야 한다

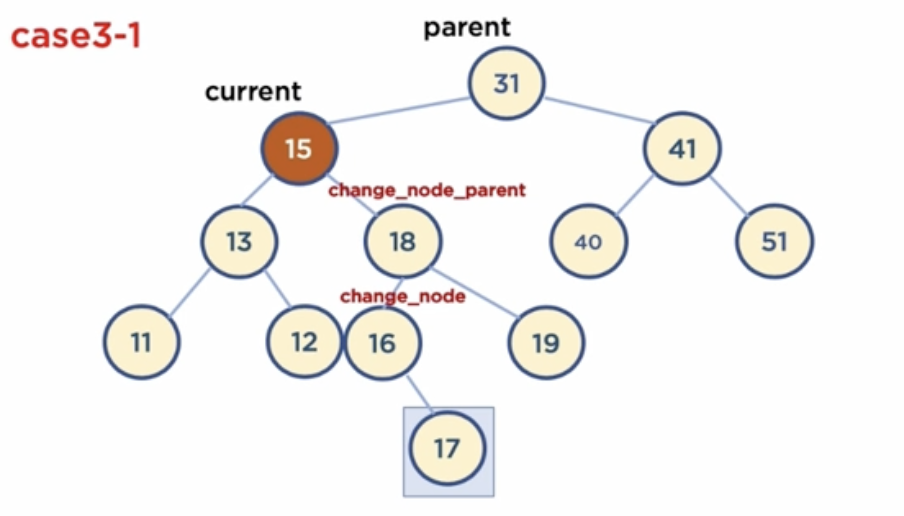
            if value < self.parent.value:
                self.change_node = self.current_node.right
                self.change_node_parent = self.current_node.right
                while self.change_node.left != None:
                    self.change_node_parent= self.change_node
                    self.change_node = self.change_node.left
                self.change_node_parent.left = None
                if self.change_node.right != None:
                    self.change_node_parent.left=self.change_node.right
                else:
                    self.change_node_parent.left = None
                self.parent.left = self.change_node
                self.change_node.right = self.current_node.right
                self.change_node.left = self.current_node.left

change_node와 change_node의 부모 노드를 생성해서
while문을 통해 제일 왼쪽으로 이동하다가
더 이상 왼쪽으로 이동할 수 없을 때의 노드에게 오른쪽 노드가있는지에 대한 유무에 따라 처리한다.
오른쪽 노드가 없으면 current_node는 change_node가 되는 것이므로
change_node의 왼쪽오른쪽은 current_node의 왼쪽 오른쪽이 되고
부모노드에서 삭제할노드가 왼쪽에 있었으니깐
부모노드의 왼쪽에 삭제할 노드 대신에 change_node가 들어간다

반대로 부모노드 오른쪽에 삭제할 노드가 있으면 지금 쓴 코드에서 부모노드에서 change_node를 오른쪽으로만 연결하면 된다.