Heap Sort는 힙의 특성을 이용하여 정렬하는 알고리즘
힙은 부모의 값이 자식의 값보다 항상 크다는 조건을 만족하는 이진 트리

1. 힙의 가장 위쪽에 위치한 루트는 힙 중에 최댓값이다
2. 형제 노드 사이에서 대소 관계는 따지지 않는다

힙을 구성할 때 중요한 포인트

원소a[i]에서
부모: a[(i-1)//2]
왼쪽 자식: a[i*2+1]
오른쪽 자식: a[i*2+2]

루트를 삭제한 힙의 재구성

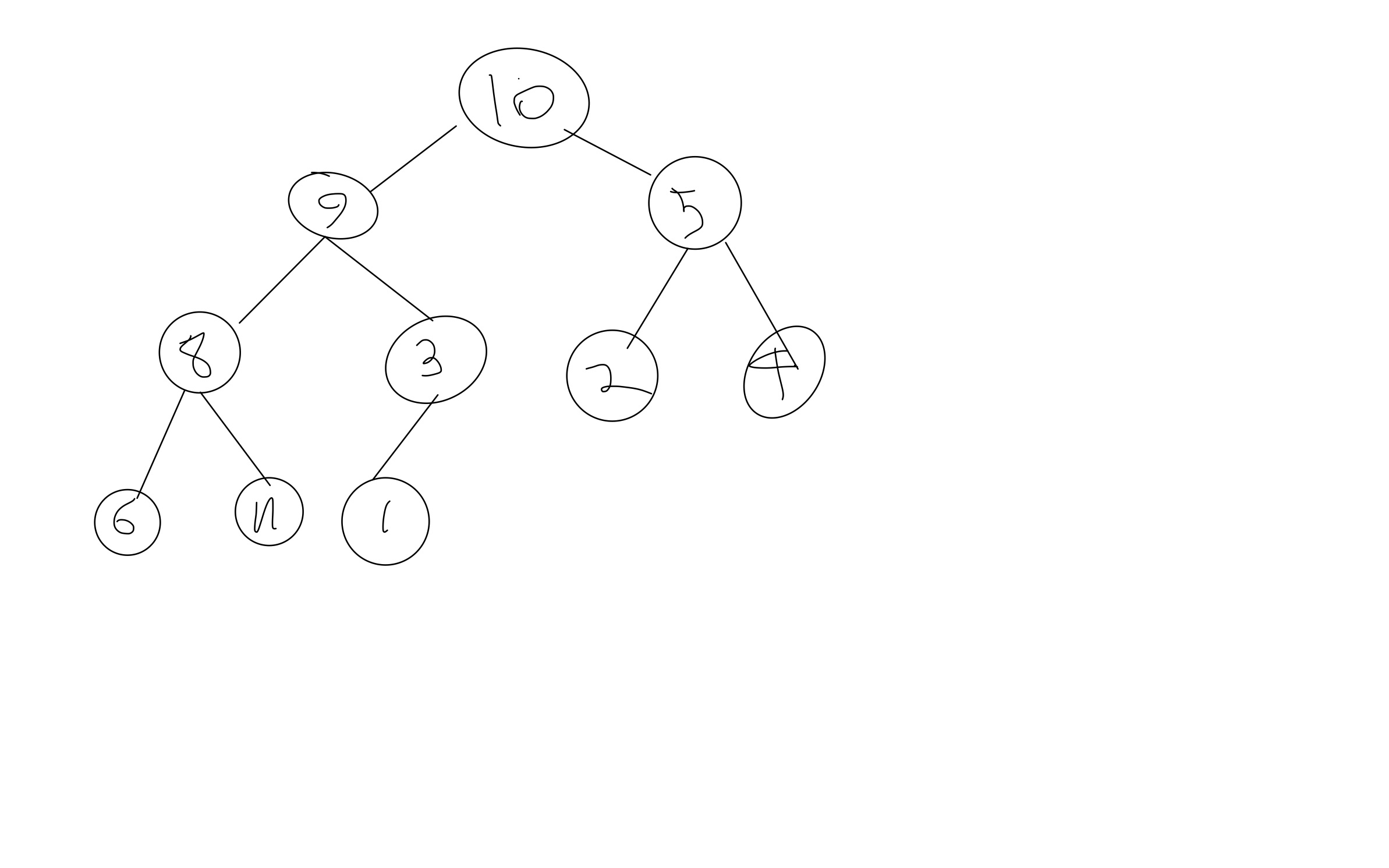
1.힙에서 루트인 10을 꺼내고, 힙의 마지막원소인 1을 10의자리로 옮김
2. 1을 앎자은위치로 이동, 이동할 1의 두 자식은 9와 5이므로 1,9,5중 최댓값이 9이므로 9와 자리를 바꿈
3. 1,8,3에서 8이 제일 크므로 8과 자리바꿈
4. 1,6,7에서 7이 제일크므로 자리바꿈

코드

Heap 설정
1. 1번째 인덱스부터 설정하므로 0번째 노드는 None으로 해둔다

class Heap:
    def __init__ (self,data):
        self.heap_array=list()
        self.heap_array.append(None) #인덱스는 1부터 시작
        self.heap_array.append(data)

2. 추가할 노드와 부모 노드를 비교하여 부모노드보다 자식노드가 크면 True를 리턴 시키는 move_up 함수 구현

    def move_up(self,inserted_idx): #노드의 위치를 판별
        if inserted_idx <=1:
            return False
        
        parent_idx = inserted_idx//2
        if self.heap_array[inserted_idx]>self.heap_array[parent_idx]:
            return True

3. 삽입 함수 구현
   예외처리 1. 삽입할 노드가 첫 노드이면 0번쨰인덱스에 None추가
   삽입할 때 필수 조건: 노드를 맨 끝의 요소에 둔다
   마지막으로 move_up함수를 통해서 부모노드보다 크면 부모노드와 위치를 바꿔주는 함수 구현

       def insert(self,data):
        if len(self.heap_array) == 0:
            self.heap_array.append(None)
            self.heap_array.append(data)
            return True
        
        self.heap_array.append(data)
        
        inserted_idx=len(self.heap_array) - 1
        while self.move_up(inserted_idx): #바꿔줘야 할 노드이면 계속해서 바꿀 수 있게
            parent_idx = inserted_idx//2
            self.heap_array[inserted_idx],self.heap_array[parent_idx] = self.heap_array[parent_idx], self.heap_array[inserted_idx]
            inserted_idx=parent_idx
        return True
       

4.삭제 함수 구현
삭제는 진짜 어제 트리만큼 어려운 것 같다.
분기를 촘촘히 해서 모든 경우를 막아내야 한다.
삭제의 경우
1. 맨 앞에 루트 노드와 맨 뒤의 노드의 위치를 바꿔준다
2. 자식 노드 오른쪽과 왼쪽과 비교하여 더 큰 값을 가진 노드와 위치를 교환한다.
3. 위치를 아래로 점 점 이동할때
1) 자식노드가 아무도 없을 때
2) 오른쪽 노드만 있을 떄
3) 왼쪽 노드만 있을 때
생각하면서 내려가야 한다.

    def move_down(self,popped_idx):
        left_child_popped_idx=popped_idx*2
        right_child_popped_idx=popped_idx*2+1
        if left_child_popped_idx>=len(self.heap_array): #자식노드가 없을 때
            return False
        elif right_child_popped_idx>=len(self.heap_array):
            if self.heap_array[popped_idx]<self.heap_array[left_child_popped_idx]:
                return True
            else:
                return False
        else:
            if self.heap_array[left_child_popped_idx]>self.heap_array[right_child_popped_idx]:
                if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
                    return True
                else:
                    return False
            else:
                if self.heap_array[popped_idx] < self.heap_array[right_child_popped_idx]:
                    return True
                else :
                    return False

    def pop(self):
        if len(self.heap_array) <=1:
            return None
        returned_data = self.heap_array[1]
        self.heap_array[1]=self.heap_array[-1]
        del self.heap_array[-1]
        popped_idx=1

        while self.move_down(popped_idx):
            left_child_popped_idx=popped_idx*2
            right_child_popped_idx=popped_idx*2+1

            if right_child_popped_idx >= len(self.heap_array):
                if self.heap_array[popped_idx]<self.heap_array[left_child_popped_idx]:
                    self.heap_array[popped_idx],self.heap_array[left_child_popped_idx]=self.heap_array[left_child_popped_idx],self.heap_array[popped_idx]
                    popped_idx = left_child_popped_idx
            else:
                if self.heap_array[left_child_popped_idx]>self.heap_array[right_child_popped_idx]:
                      self.heap_array[popped_idx],self.heap_array[left_child_popped_idx]=self.heap_array[left_child_popped_idx],self.heap_array[popped_idx]
                      popped_idx = left_child_popped_idx
                else:
                    if self.heap_array[popped_idx] < self.heap_array[right_child_popped_idx]:
                        self.heap_array[popped_idx],self.heap_array[right_child_popped_idx]=self.heap_array[right_child_popped_idx],self.heap_array[popped_idx]
                        popped_idx=right_child_popped_idx
        return returned_data