동적 프로그래밍

동적 프로그래밍

하위 문제가 중첩되는 재귀 문제를 최적화하는 절차

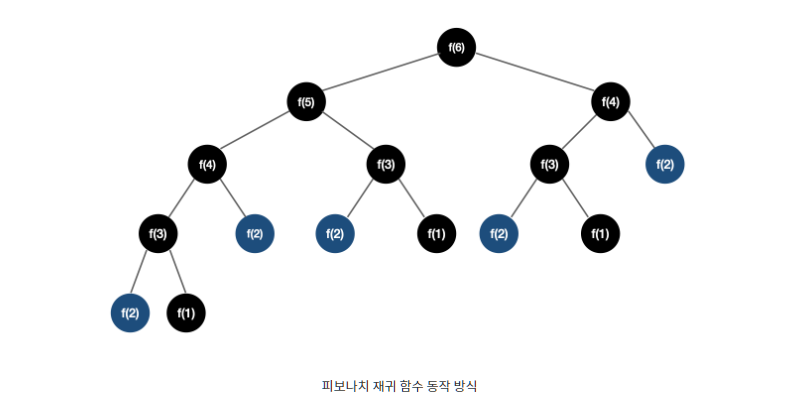
피보나치 수열을 재귀로 표현 하면 아래와 같이 표현된다.

public class Simple {

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		dp  = new int[n+1];
		System.out.println(fibo(n));
	}
	
	// 단순 재귀
	static int fibo(int x) {
		if( x ==1 || x==2) return 1;
		return fibo(x-1) + fibo(x-2);
	}
}

이때, 같은 함수를 여러번 반복하여 호출하므로 시간복잡도 $O(2^n)$을 갖게 된다.

DP 문제가 성립할 조건

1. 최적 부분 구조
   • 상위 문제를 하위 문제로 나눌 수 있으며 하위 문제의 답을 모아서 상위 문제를 해결할 수 있다.
2. 중복되는 부분 문제
   • 동일한 작은 문제를 반복적으로 해결해야 한다.

동적 프로그래밍을 통한 알고리즘 최적화에는 일반적으로 두 가지 방법이 사용된다.

Top-down(하향식)

상위 문제를 해결하기 위해서 하위 문제를 재귀적으로 호출하여 하위 문제를 해결함으로써 상위 문제를 해결하는 방식이다. 이 때 해결해놓은 하위 문제를 저장해 놓기 위해 Memoization이 사용된다.

public class Topdown {
	static int[] dp;
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		dp  = new int[n+1];
		System.out.println(fibo(n));
		
	}
	
    // Top-down
	static int fibo(int x) {
		if( x ==1 || x==2) return 1;
		if(dp[x] != 0) return dp[x];
		dp[x] = fibo(x-1) + fibo(x-2);
		return dp[x];
	}
}

Bottom-up(상향식)

하위에서부터 문제를 해결해나가면서 먼저 계산했던 문제들의 값을 활용해서 상위 문제를 해결해나가는 방식으로 DP의 전형적인 형태는 Bottom-up이다. 여기서 사용되는 문제 결과 값 저장용 리스트는 DP 테이블이라고 부른다.

public class Bottomup {

	static int[] dp;
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		dp  = new int[n+1];
		
		System.out.println(fibo(n));
	}
	
    // Bottom-up
	static int fibo(int x) {
		dp[1] =1;
		dp[2] =1;
		for(int i=3; i<x+1; i++) {
			dp[i] = dp[i-1] + dp[i-2];
		}
		return dp[x];
	}
}

Memoization(메모이제이션)

한 번 계산한 결과를 메모리 공간에 메모하는 기법

메모이제이션 특징

• 같은 문제를 다시 호출 하면 메모했던 결과를 그대로 가져온다
• 값을 기록해 놓는다는 점에서 캐싱(Cachig)이라고 한다
• DP에만 국한된 개념이 아니다. 한 번 계산된 결과를 담아 놓기만 하고 DP가 아닌 다른 방식으로도 사용될 수 있다. (캐싱,메모이제이션)
  
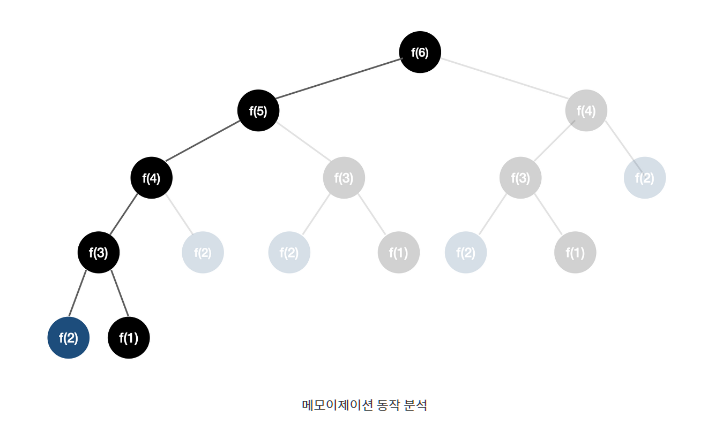
  출처: https://loosie.tistory.com/150