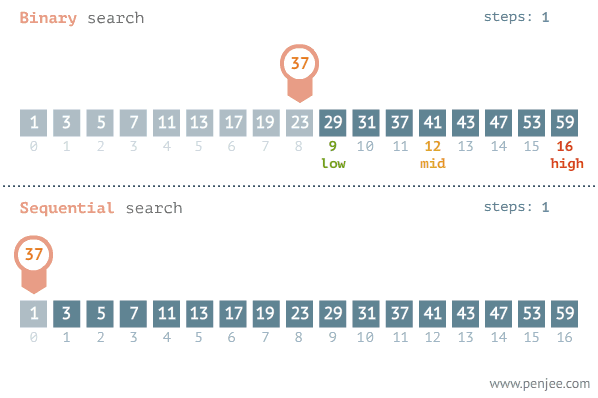
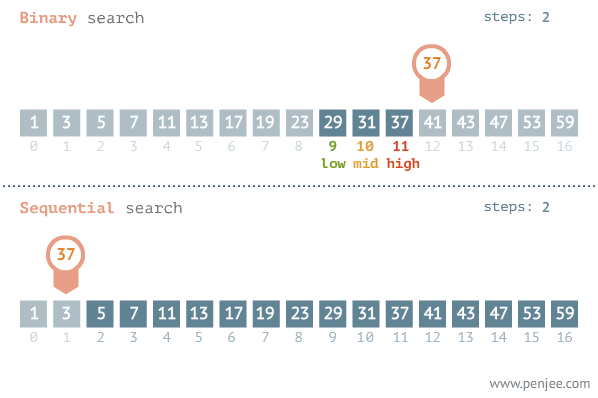
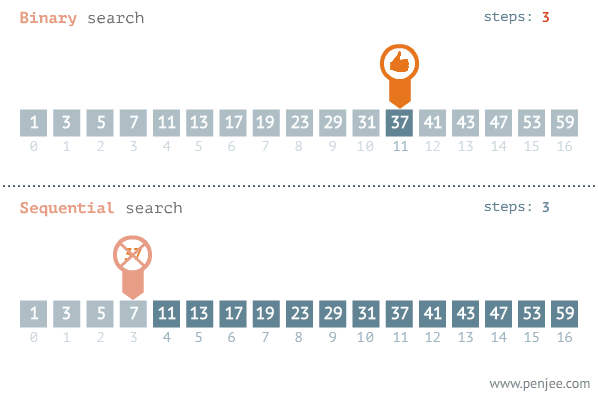
이진탐색과 순차탐색 비교
이진탐색(binary search)
- BigO - O(LogN)
- 정렬된 자료를 반으로 나누어 탐색하는 방법
- 주의사항 : 자료는 반드시 오름차순으로 정렬된 자료여야 한다.
순차탐색(linear search)
- BigO - O(N)
- 순서대로 찾는다. 성능평가시 비교대상으로 사용하고 정렬방식이 상관 없다.
순차탐색의 예시
finding_target = 14
finding_numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]
def is_existing_target_number_sequential(target, array):
for number in array:
if target == number:
return True
return False
result = is_existing_target_number_sequential(finding_target, finding_numbers)
print(result)
이진탐색의 예시
finding_target = 14
finding_numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]
def is_existing_target_number_binary(target, array):
current_min = 0
current_max = len(array) - 1
current_guess = (current_min + current_max) // 2
while current_min <= current_max:
if array[current_guess] == target:
return True
elif array[current_guess] < target:
current_min = current_guess + 1
else:
current_max = current_guess - 1
current_guess = (current_min + current_max) // 2
return False
result = is_existing_target_number_binary(finding_target, finding_numbers)
print(result)
- 이진 탐색을 반복할수록 남아있는 탐색할 자료의 개수는 1/2로 줄어든다.
- 1번째 실행시 탐색할 남은 자료의 개수: N
- 2번째 실행시 탐색할 남은 자료의 개수: N/2
- 3번째 실행시 탐색할 남은 자료의 개수: N/2 * 1/2
- 4번째 실행시 탐색할 남은 자료의 개수: N/2 1/2 1/2
- K번째 실행시 탐색할 남은 자료의 개수: N*(1/2)^K
- 탐색이 끝나는 시점에는 남은 자료의 개수가 1이 되어야 한다. 따라서 N*(1/2)^K = 1
- 양 변에 2^K를 곱해주면 2^K = N > K = log2^N
- K의 의미는 실행횟수 따라서 자료의 갯수 N에 따른 시행횟수는 log2^N
시간 복잡도는 BigO 표기법으로 O(logN) 으로 나타낼 수 있다.