[자료구조] 트리 (Tree)

트리(tree)

트리는 방향 그래프의 일종으로 정점을 가리키는 간선이 하나 밖에 없는 구조를 가지고 있다.

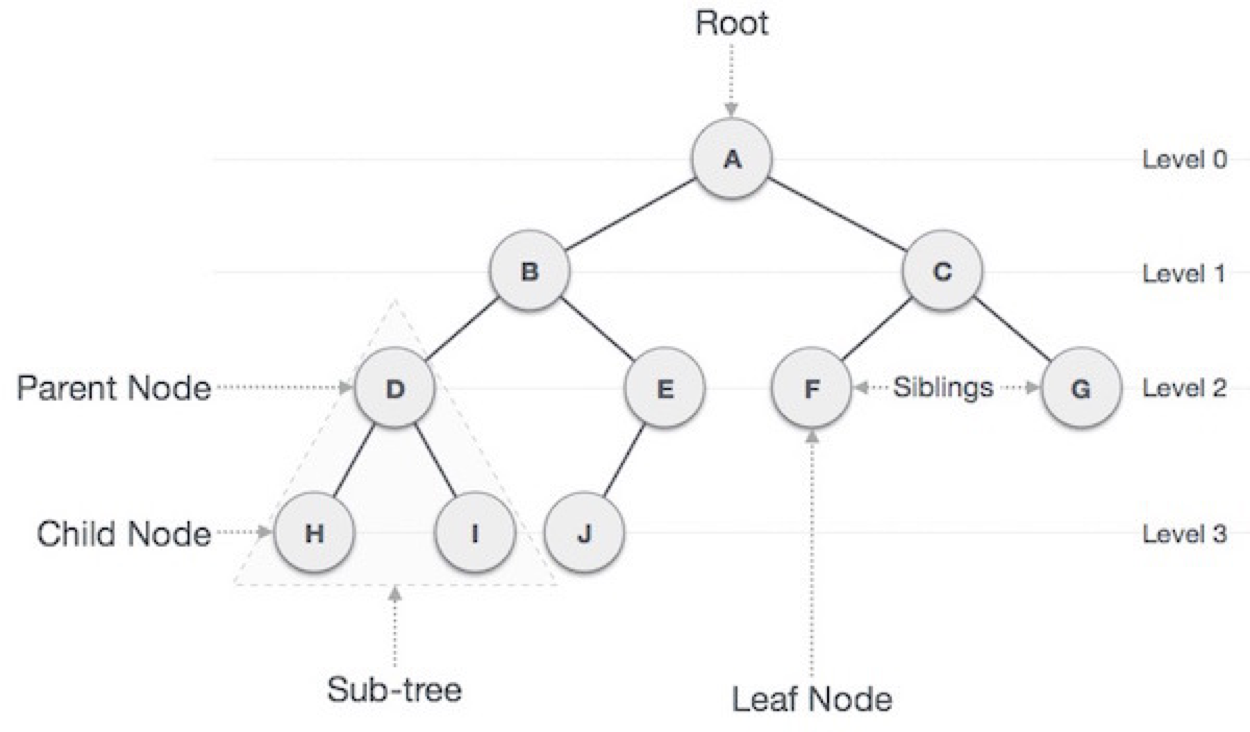
Root : 트리 구조의 시작점이 되는 노드(가장 상위 부모)
Node : 트리 구조를 이루는 모든 개별 데이터
Edge : 노드를 연결하는 선 (간선)
Leaf Node : 트리 구조에서 자식이 없는 노드(가장 하위 자식)
depth : 루트 노드에서 어떤 노드까지 도달하기 위해 거쳐야 하는 간선의 수
Lvevl : 레벨은 Root(0레벨)에서 몇번째 깊이 인지 나타낸다. 같은 깊이를 가지고 있는 노드를 묶어 레벨로 표현할 수 있다.
Degree : 한 정점에서 뻗어나온 간선의 수(자식 노드의 수)

트리의 특징

• 루트 정점을 제외한 모든 정점은 반드시 하나의 부모 정점을 가진다.
• N개의 노드를 가진 이진 트리는 반드시 N-1개의 간선을 가진다.
• 루트에서 특정 정점으로 가는 경로는 유일하다.

트리의 종류

이진 트리 (Binary Tree)

• 부모 노드가 자식 노드를 최대 2개 갖고 있는 트리이다.

완전 이진 트리 (Complete Binary Tree)

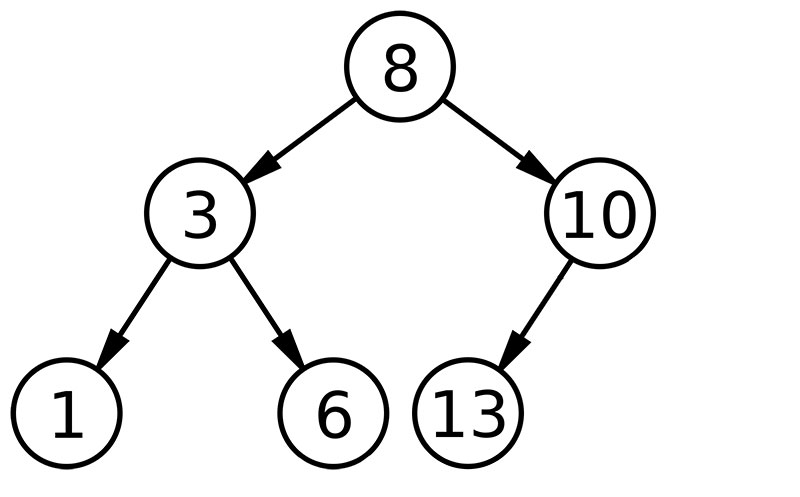
• 완전 이진 트리는 마지막 레벨을 제외하고 모든 레벨이 완전히 채워진 트리이다.
• 노드가 왼쪽에서 오른쪽으로 채워져야 한다.
• 완전 이진트리는 배열을 사용해 효율적으로 표현이 가능한다.

포화 이진 트리 (Perfect Binary Tree)

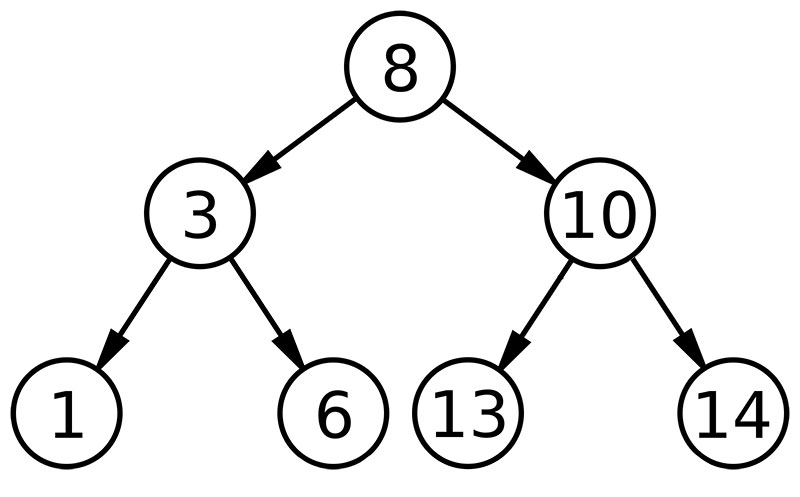
• 마지막 레벨의 노드를 제외하고 모든 노드가 2개의 노드(자식)을 가지는 트리
• 마지막 레벨의 노드까지 모두 채워져 있는 트리이다.

편향 트리 (skewed tree)

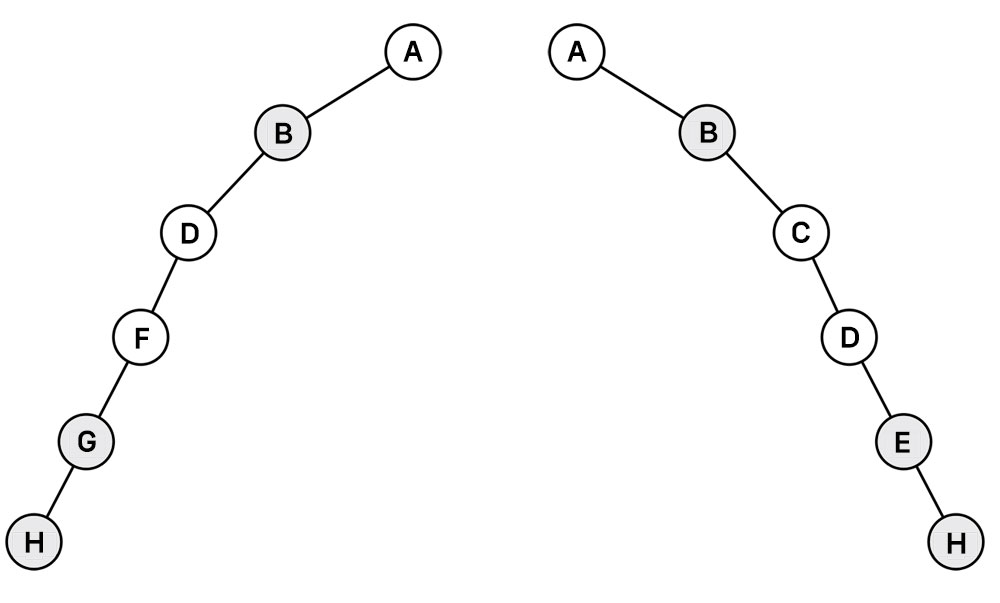
• 모든 노드들이 자식을 하나만 가진 트리
• 편향 트리는 모든 노드가 루트(부모) 노드의 왼쪽 자식 노드이거나 오른쪽 자식 노드인 경우와 같다.

이진 트리의 특징

• 정점이 N개인 이진 트리는 최악의 경우 높이가 N이 될 수 있다.
• 정점이 N개인 포화 또는 완전 이진 트리의 높이는 log N이다.
• 높이가 h인 포화 이진 트리는 2h - 1개의 정점을 가진다.

배열로 간단하게 구현하는 이진트리

// 편의상 0번 Index는 비워두고 시작한다.
// leftChild = Index * 2
// rightChild = Index * 2 + 1
// parent = Math.floor(Index / 2)
const tree = [null,8,4,5,2,3,1];