[DP] LEETCODE.494 TARGET SUM

[ 문제설명 ]

[ 문제해결 #1 ]

BackTracking

각 인덱스별 숫자에 따라 +/-의 조합으로 풀 수BackTraking 방식으로 풀게 되면 O(2^n)의 시간복잡도가 예상된다. 사실 최초 제시된 n의 값이 20이었기 때문에 2^20이더라도 1억 미만의 값이 산출되므로 시간복잡도 상 문제가 되지 않을 것이라 예상하였다.

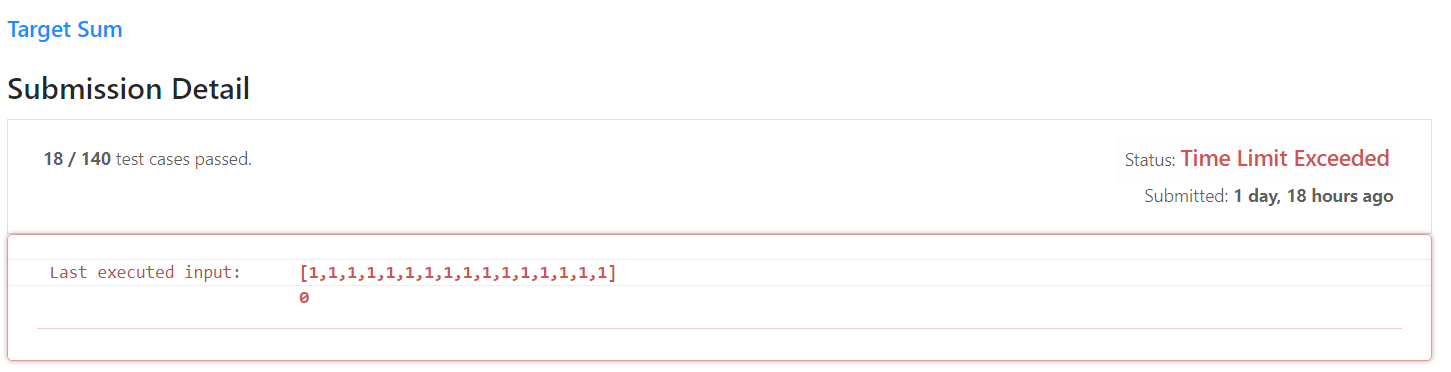
BackTracking 방식으로 푼 방식은 아래와 같으며 예상과 달리 TLE 발생하였다.

Backtracking 기반 풀이법

class Solution(object):
    def findTargetSumWays(self, nums, target):
        sumval,answer=0,[]
        len_num=len(nums)
        if len_num<1 :
            return 0
            
        self.backtrack(target,sumval,answer,-1,len_num,nums)
        
        return len(answer)
        
        
    def backtrack(self,target,sumval,answer,i,len_num,nums):

        if i is -1:
            
            self.backtrack(target,nums[i],answer,0,len_num,nums)
            self.backtrack(target,nums[i]*(-1),answer,0,len_num,nums)
            return
        if i >= len_num :
            return
        if i is len_num-1 and sumval == target:
            answer.append(1)
        plus_sumval , minus_sumval = sumval+nums[i],sumval-nums[i]
        self.backtrack(target,plus_sumval,answer,i+1,len_num,nums)
        self.backtrack(target,minus_sumval,answer,i+1,len_num,nums)
        

[문제해결 #2]

나의 현재 상태 관점에서 내가 찾고자 하는 것에만 집중한다
위 문장은 DP 문제를 접근할 때 가지고 있는 나의 개인적인 철학과도 같다.

BackTracking 방식이 TLE가 발생했던 것은 최초 Test Case인 [1,1,1,1,1]과 같이 조합에 따라 이전 결과가 중복되는 부분이 있고 이로 인한 비효율이 그 원인이라고 생각이 들었다.

내가 찾고자 하는 것은 상세한 조합 결과가 아니고 단순 조합의 수이다. 즉 상세한 조합 결과를 찾고자 한다면 +/-를 각 수에 계산해나가면서 Target 값에 도달하면 Count+1를 해줘야 하나 단순 조합의 수라면 나의 현재 상태에서 이전의 결과 값을 활용하기만 하면 된다라고 생각했다.

그러면 나의 상태를 정의해야 한다. 해당 문제에서 나의 상태는 nums 배열의 인덱스였다. 즉 i 번째 숫자를