문제
https://leetcode.com/problems/shortest-palindrome/
상기 문제는 주어진 문자를 회문(Palindrome)으로 변환하기 위한 최소한의 문자를 판단하여 추가하는 문제이다.
문제풀이
#시간 초과 알고리즘
class Solution:
def shortestPalindrome(self, s: str) -> str:
l=0
r=len(s)-1
while(l<r):
if s[l]==s[r]:
l2=l
r2=r
while(s[l2]==s[r2]):
if l2>=r2:
return s[r+1:][::-1]+s
break
l2+=1
r2-=1
l=0
r-=1
return s[r+1:][::-1]+s
#Rolling Hash 알고리즘
class Solution:
def shortestPalindrome(self, s: str) -> str:
if not s:
return ""
mod = 10**9 + 7
dp, inv_dp = 0, 0
result_index = 0
power = 1
for i in range(len(s)):
dp = (dp + hash(s[i])*power) % mod
inv_dp = (inv_dp *10 + hash(s[i])) % mod
power = (power * 10) % mod
if dp == inv_dp:
result_index = i + 1
return s[result_index:][::-1] + s
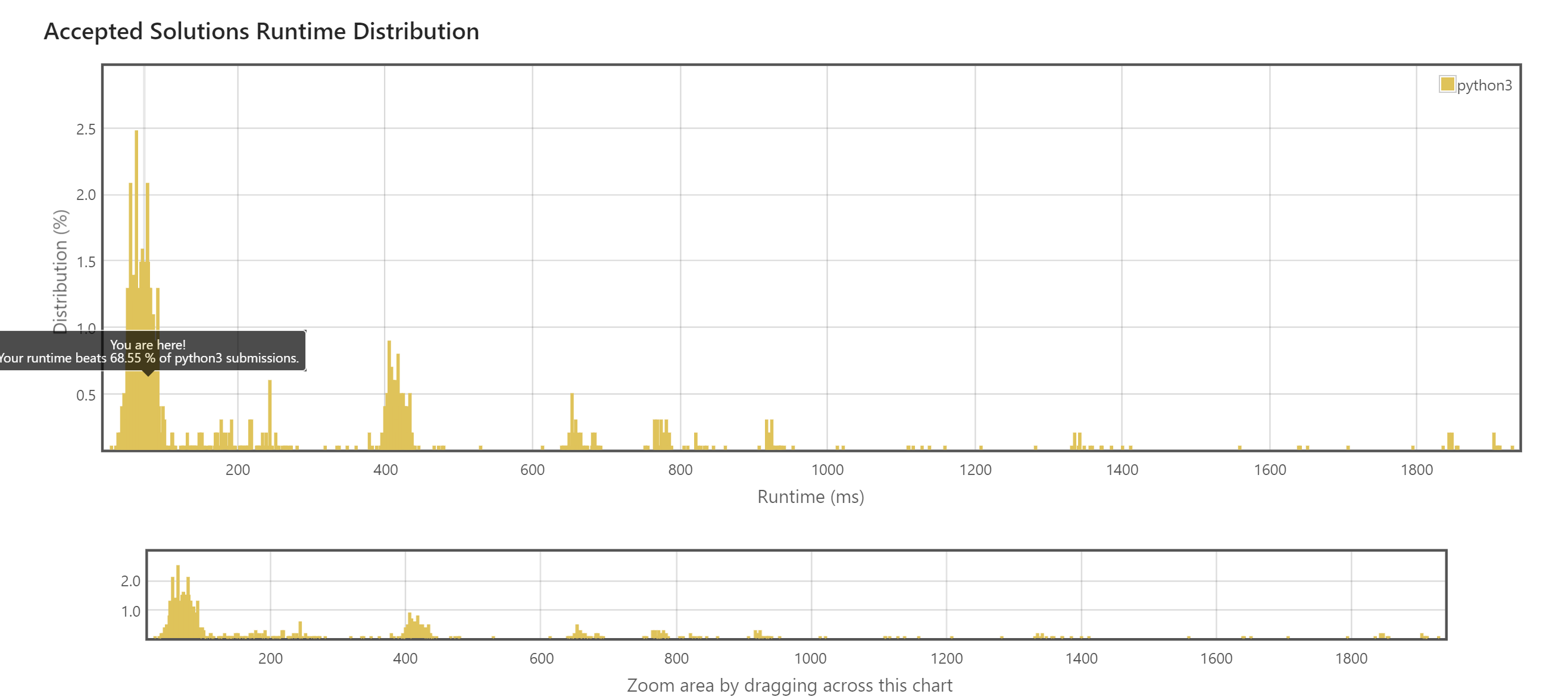
핵심 코드 설명
이 문제는 좌측에서만 문자를 추가해야 하는 조건이 존재하므로 첫번째 인덱스 값을 시작점으로 갖는 가장 긴 회문을 찾은 후 잔여 문자를 좌측에 삽입하면 해결이 가능한 문제였다.
다만 문제는 이러한 형태를 어떻게 효율적으로 찾을 것인가가 핵심문제였다.
최초 나는 위 소스 중 첫번째인 반복문을 통해 판단을 하였으나 aaa..aa등으로 무수히 긴 문자가 존재하는 경우 매번 동일한 판단을 여러번 해야 하는 비효율이 존재하였다. (아래 표 참조)

이를 해결하기 위해 Rolling Hash 기법을 통해 접근하였다.
로직을 간단히 설명해보자면 아래와 같다.
1. idx 0에서 시작점을 갖는 가장 긴 Palindrome을 찾기 위해 탐색 범위를 늘려간다.
2. 탐색 범위가 정해지고 나면 정순과 역순 기준으로 각각 Hash 값을 산출한다. 단 여기서 중복 계산을 막기 위해 dp 메모이제이션 개념을 활용한다.
즉 정순 방향인 경우 기존 값 + 추가되는 문자의 hash값을 위치를 반영(10^i)하여 더한다. 역순 방향의 경우 기존 값을 Shifting한 후 추가되는 문자의 Hash 값을 더한다.
3. 최종적으로 동일한 i에 대해 정순/역순 값이 같은 것 중 가장 큰 i가 시작 인덱스가 0인 가장 긴 회문이 된다. 이를 활용하여 좌측에 잔여 문자의 역순을 더해 Return한다.
단, 큰 숫자 방지를 위해 Mod 처리를 수반하여야 Time Exceed 발생하지 않음
Lookback
- Palindrome 문제의 경우 Dp,Manacher Algorithm 등 다양한 풀이범이 있다. 하나씩 차근차근 스터디해 볼 필요가 있을 것 같다.
- 이번 문제는 String Matching과 관련된 문제였다. 이러한 류의 문제에는 흔히 KMP 알고리즘을 통해 O(n)으로 해결이 가능하다고 하는데 강의로 봐선 이해가 잘 안가지만 좀 더 시간을 들여 확인해봐야겠다.
