이진 탐색 트리란?
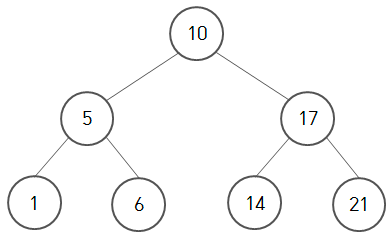
- 각 노드의 왼쪽 자식은 부모보다 작다.
- 각 노드의 오른쪽 자식은 부모보다 크다.
- 각 노드의 자식이 2개 이하
- 중복된 노드가 없어야 함
- 검색 목적 자료구조인데, 굳이 중복이 많은 경우에 트리를 사용하여 검색 속도를 느리게 할 필요가 없습니다. 트리에 삽입하는 것보다, 노드에 count값을 가지게 하여 처리하는 것이 훨씬 효율적입니다.
이진 탐색 트리의 최소값
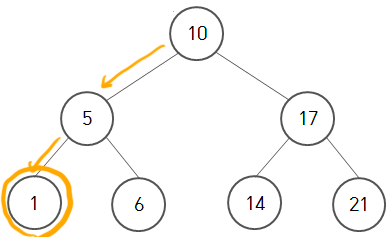
이진 탐색 트리의 가장 왼쪽에 존재 → 모든 노드는 자신의 왼쪽에 자신보다 작은 값을 가져야 하기 때문이다.
이진 탐색 트리의 최대값
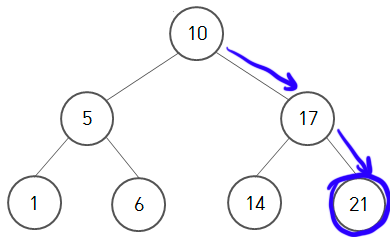
트리의 가장 오른쪽에 존재 → 모든 노드는 자신의 오른쪽에 자신보다 큰 값을 가지기 때문이다.
이진 탐색 트리 순회 방법
순회란? 모든 노드들을 한번씩 방문하는 것을 의미한다.
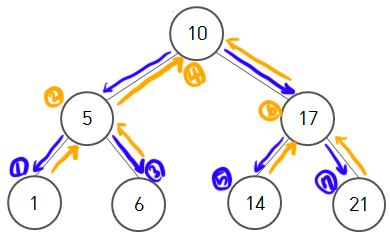
중위 순회 (inorder traversal)
루트 노드를 기준으로 왼쪽 서브 트리로 가다가 더 이상 왼쪽 서브트리가 없으면 현재 노드를 방문해서 처리할 일들을 처리한 후 그 노드의 오른쪽 서브트리로 간다. 오른쪽 서브트리가 없다면 루트 트리로 이동 후 다시 중위 순회를 한다.
위의 출력 순서를 보면 1 → 5 → 6 → 10 → 14 → 17 → 21
이진 탐색 트리의 값들을 순서대로 방문을 한다는 특징이 있다.
노드의 successor(후임자)
해당 노드보다 값이 큰 노드들 중에서 가장 값이 작은 노드
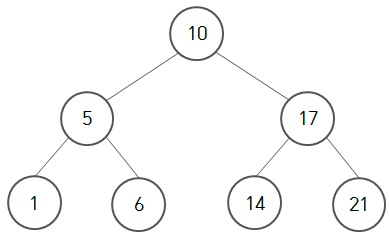
- 10의 successor : 14
- 6의 successor : 10
- 5의 successor : 6
노드의 predecessor(선임자)
해당 노드보다 값이 작은 노드들 중에서 가장 값이 큰 노드
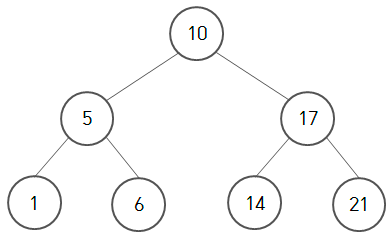
- 10의 predecessor : 6
- 6의 predecessor : 5
- 5의 predecessor : 1
추가하기
이진 검색 트리를 생성하기 위해 노드를 추가할 때 쓸 insert함수
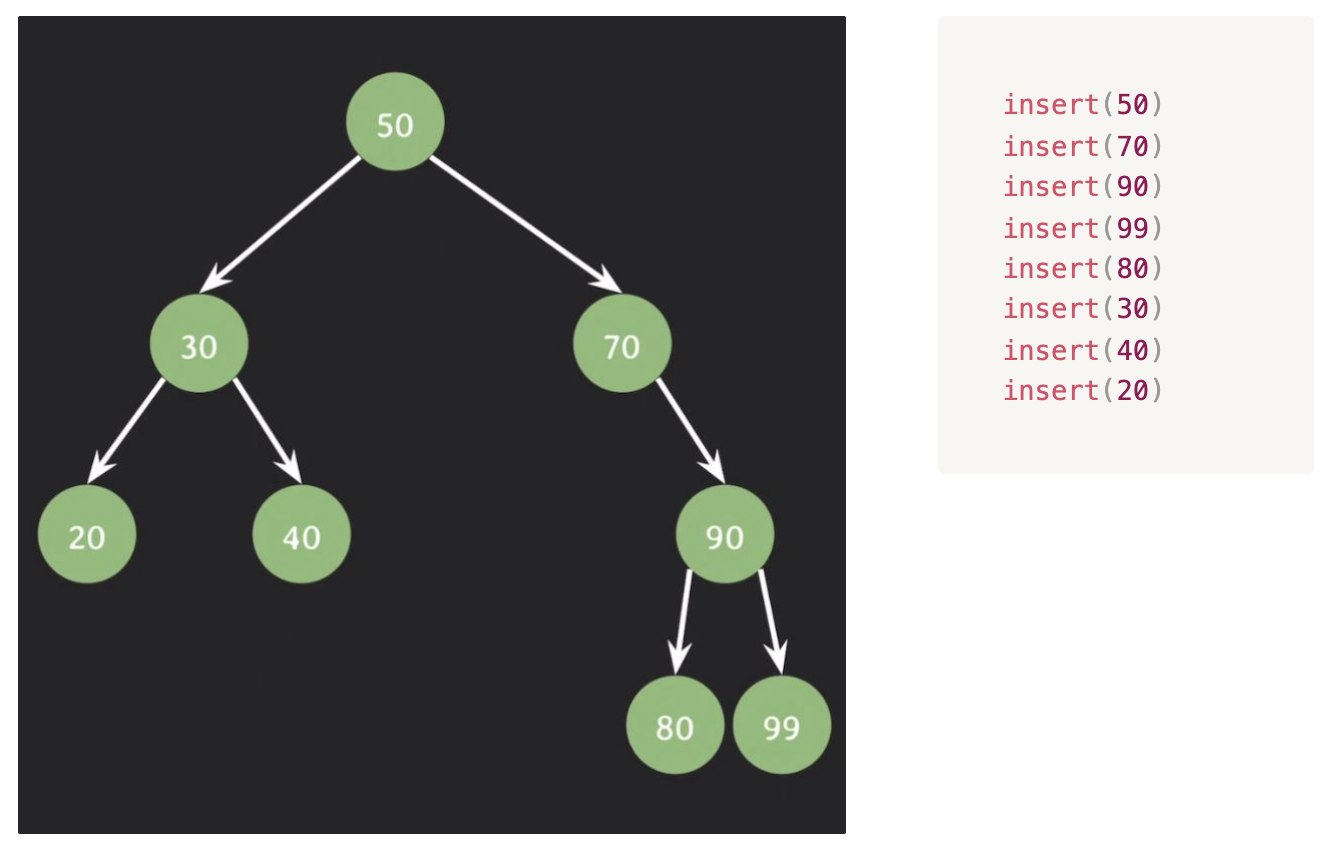
삭제하기
삭제하려는 노드가 있는지 검색 → 있으면 삭제
결국 삭제가 검색을 동반한다. 삭제를 알면 자연스럽게 검색이 이해된다.
삭제의 3가지 Case
- 자식이 없는 노드일 때 → 그냥 삭제
- 자식이 1개인 노드일 때 → 지워진 노드에 자식을 올리기
- 자식이 2개인 노드일 때 → 오른쪽 자식 노드에서 가장 작은 값 or 왼쪽 자식 노드에서 가장 큰 값 올리기
1. 자녀가 없는 노드를 삭제
delete(20)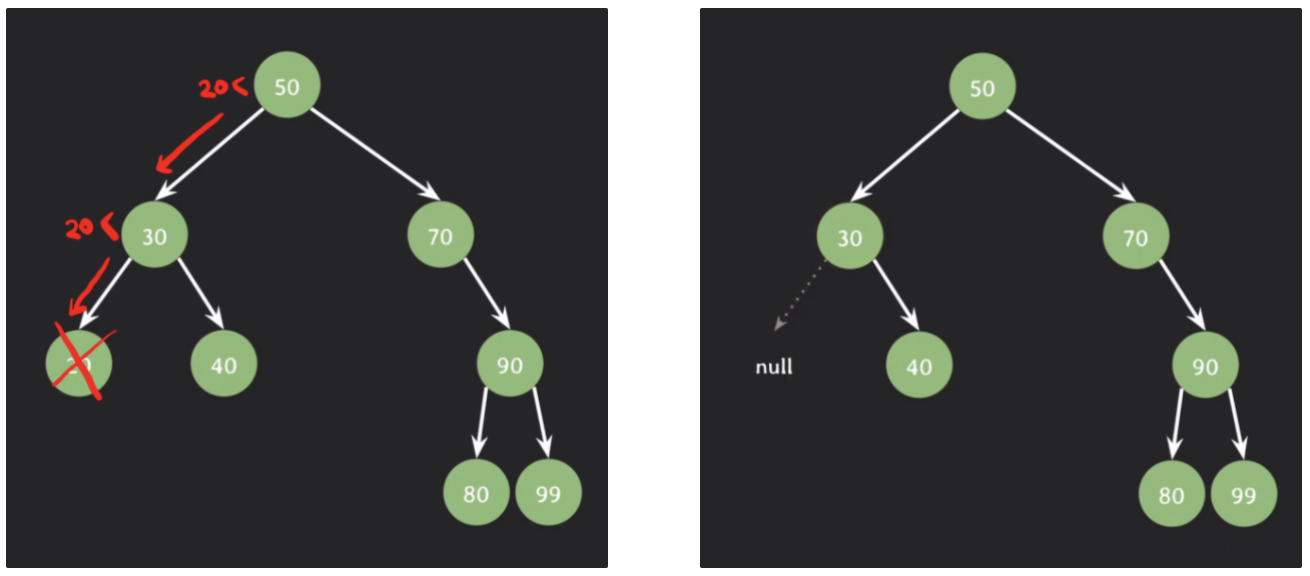
삭제될 노드를 가리키던 레퍼런스를 가리키는 것이 없도록 처리
2. 자녀가 하나인 노드 삭제
delete(30)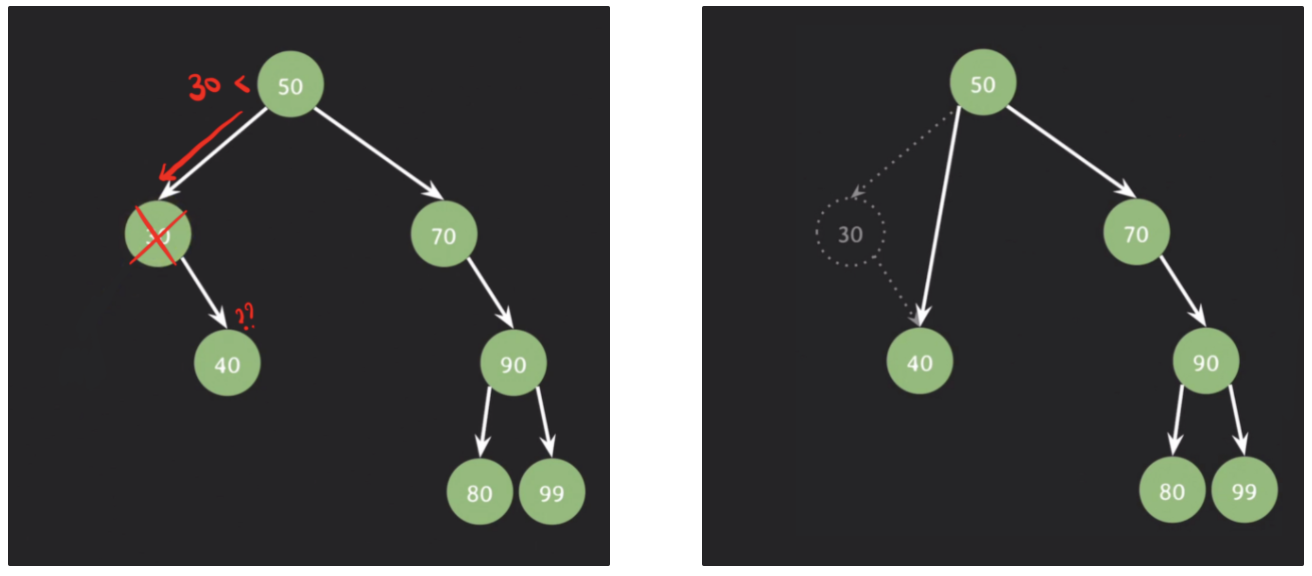
삭제될 노드를 가리키던 레퍼런스를 삭제될 노드의 자녀를 가리키게 변경
3. 자녀가 둘인 노드 삭제
삭제될 노드의 오른쪽 서브 트리에서 제일 값이 작은 노드가 삭제될 노드를 대체한다.
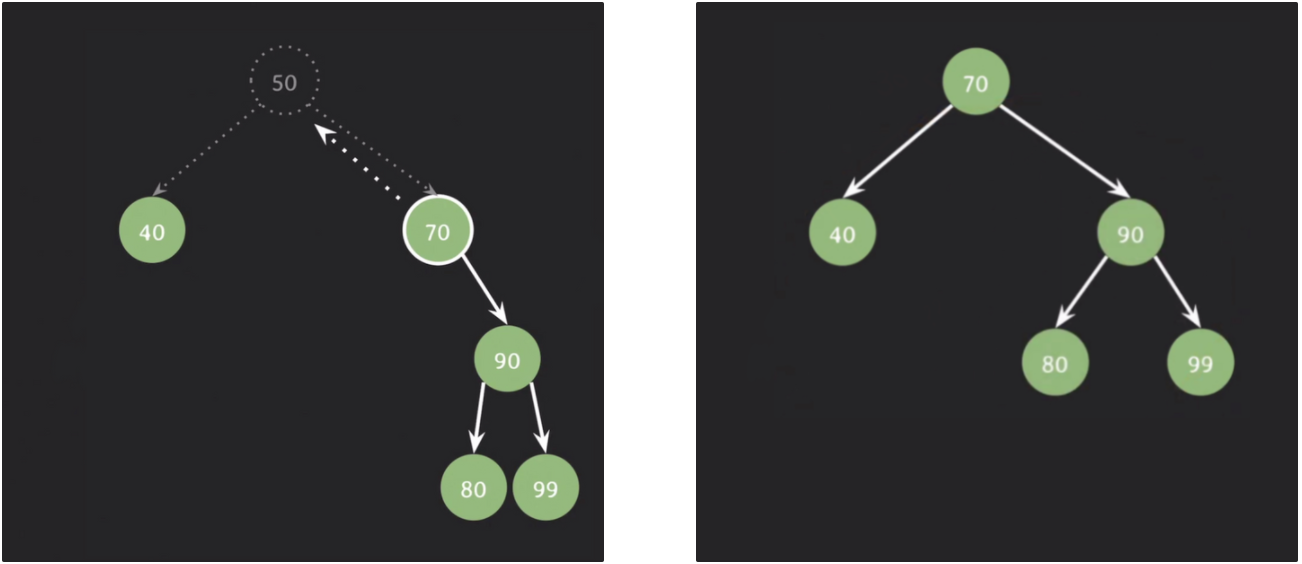
위의 상태에서 85를 추가하고 70을 삭제한다면
add(85)
delete(70)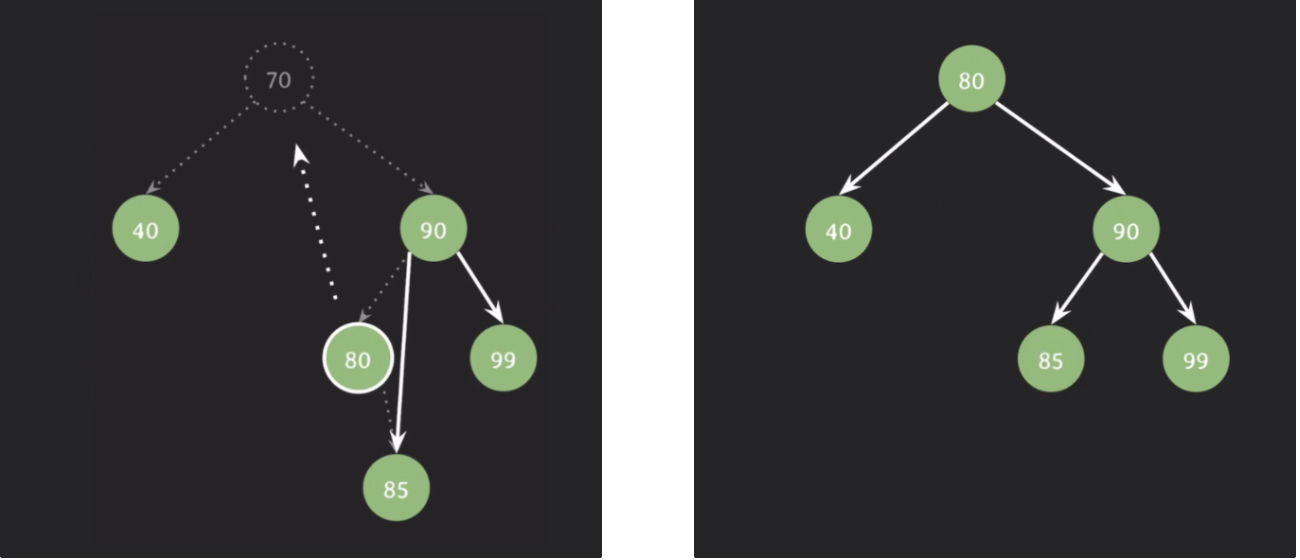
중요한 것은 삭제가 되더라도 이진 탐색트리의 특징이 유지돼야 한다는 것이다.
이진트리의 장정
- 삽입 삭제가 유연하다
- 값의 크기에 따라 좌우 서브트리가 누눠지기 때문에 삽입/삭제/검색이 보통은 빠르다.
- 값의 순서대로 순회가 가능하다.

