문제

DP문제인지 그래프 문제인지 헷갈렸던 문제
https://www.acmicpc.net/problem/1890

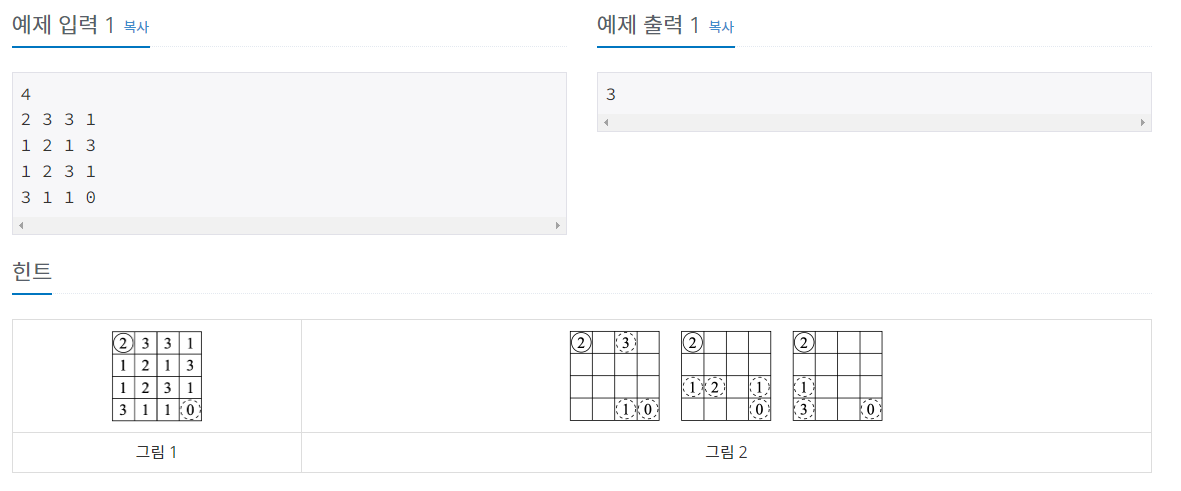
이런식으로 그래프가 주어지는데, 각 칸에는 이동할 때 건너뛰는 거리가 주어진다.
즉 이동의 규칙이

• (0,0) 좌표에서 시작하는데 무조건 오른쪽 혹은 아래쪽으로 이동해서 (N-1, N-1) 좌표에 도착해야 한다.
• 그런데 한번 이동할 때에는 현재 칸에 적혀있는 숫자만큼 무조건 건너뛰어야 한다.

딱봐도 모양새가 그래프로 풀면 될거같이 생겨서 처음에는 DFS로 구현했다.

왜 DFS냐면

이문제는 최단경로나 하나의 경로만 찾는것이 아닌 모든 경우의 수를 다 구해야 하므로 어차피 완전탐색을 해야하는건 BFS를 쓰나 DFS를 쓰나 같다.
하지만 BFS를 쓰면 메모리를 많이 차지할 뿐더러 최단경로를 찾는 이점 또한 활용할 수 없기에 DFS를 사용했다.

그래프탐색이론 리마인드 해보자면
DFS는 이렇게 무지성으로 한가지 루트만 저장하면서 탐색하면 되지만

BFS는 모든 경로를 저장하면서 탐색하기 때문에 최단경로를 바로 찾을 수 있는 장점이 있지만 메모리를 많이 차지한다.

첫번째 시도

import sys
"""
DFS (시간초과)
"""
N = int(sys.stdin.readline())
graph = list()
for _ in range(N):
    graph.append(list(map(int, sys.stdin.readline().split())))
stack = list()
answer = 0
stack.append((0, 0))
while stack:
    y, x = stack.pop()
    dist = graph[y][x]
    if y == N-1 and x == N-1:
        answer += 1
        continue
    for dir in [(1, 0), (0, 1)]:
        tar_y, tar_x = y + (dist * dir[0]), x + (dist * dir[1])
        if tar_y >= N or tar_x >= N:
            continue
        stack.append((tar_y, tar_x))
print(answer)

스택을 이용한 매우 정석적인 DFS 로 모든 경우의 수를 완전탐색, 목적지에 도착하면 카운트를 1 증가시켰다. 딱히 뭐 설명할건 없는거같다.
조금 다른점이라면 이동방향이 아래, 우측방향 두가지 라는점.

두번째 시도

조금 더 효율적인 풀이를 해보자. (사실 DP 문제로 분류되어있기 때문에 이게 정석이긴 하다.)

일반적인 그래프 탐색에서는 모든 방향으로 이동이 가능하기 때문에 DFS나 BFS를 사용해서 이동경로를 메모리에 저장해두어야 한다.
그러나 이 문제에서는 이동경로가 딱 두 가지 케이스로 고정되는 특징이 존재한다.
그 말의 뜻은 A -> B로 이동한다고 했을 때 B 입장에서는 들어오는 방향이 딱 두 가지 케이스로 정의되고 그 두 가지 경우만 체크해보면 되기 때문에 굳이 이동방향을 메모리에 저장해두지 않아도 된다.
즉, B 입장에서 위에서 들어오는경우, 왼쪽에서 들어오는 경우 두 가지로 점화식을 세울 수 있다는 뜻.

• dp배열은 graph와 똑같은 모양을 하고 graph의 각 칸에 도달할 수 있는 경우의 수를 저장한다.
• 나머지는 0, (0, 0) 시작점을 1로 초기화한다. (모두 0인 상태에서 항상 시작점부터 시작하므로)
• 좌측에서 우측, 위에서 아래 방향으로 순서대로 보면서,현재 시점에서 갈 수 있는 목적지 두 곳에 경우의 수를 더해나간다.

"""
DP (정해)
"""
N = int(sys.stdin.readline())
graph = list()
dp = [[0 for i in range(N)] for j in range(N)]
for _ in range(N):
    graph.append(list(map(int, sys.stdin.readline().split())))
dp[0][0] = 1

# 이동방향이 좌측에서 우측, 상단에서 하단으로 고정인 특징이 있으므로, 
# 가장 상단부터 우측방향으로 차례대로 훑고 지나가도 문제가 없다.
for y in range(N):
    for x in range(N):
        if y == N-1 and x == N-1:
            continue	# 마지막 목적지의 값이 0이면 무한루프를 돌기 때문에 빠져나와준다.
        dist = graph[y][x]
        for dir in [(1, 0), (0, 1)]:
            tar_y, tar_x = y + (dist * dir[0]), x + (dist * dir[1])
            if tar_y >= N or tar_x >= N:
                continue
            dp[tar_y][tar_x] += dp[y][x]
print(dp[-1][-1])

결과

DFS로 풀었을 때 테스트케이스는 통과했지만 결과적으로 시간초과가 나왔다.
DFS의 시간복잡도는 O(V+E)인데, 이 그래프는 정점의 수가 $N^2$개이고 각 정점마다 2개의 노드가 존재하므로 $V = N^2, E = 2\times N^2$ 가 된다.
DP의 경우 2차원 배열을 한번만 훑으면 되므로 시간복잡도는 $O(N^2)$가 된다.
DFS역시 $V+E = 3N^2$이고 시간복잡도에서 상수는 생략하므로 똑같이 $O(N^2)$라고 볼 수 있찌만 실제로는 DP에 비해 같은 반복문이 3배로 돌아가기 때문에 시간초과가 나는것 같다.

배운점
그래프 탐색 문제라도 이동의 규칙이 있고 제한시간이 부족한 경우라면 DP형식으로 풀 수 있는지 고려해보자.