Source Transformation(전원의 변환)

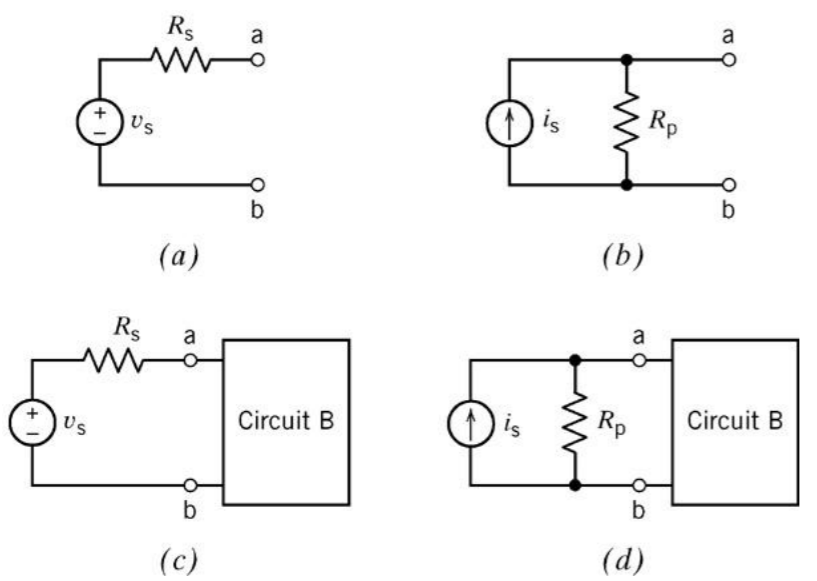
위의 그림에서 a,b처럼 생긴 회로가 있을 때, 두 회로에 circuit B를 연결시켜서 작동이 잘 된다고 생각해보자. 이때 특정 조건에서 Circuit B가 c,d에서 똑같은 작업이 된다고 할 때, a,b를 equivalent(등가)라고 한다.

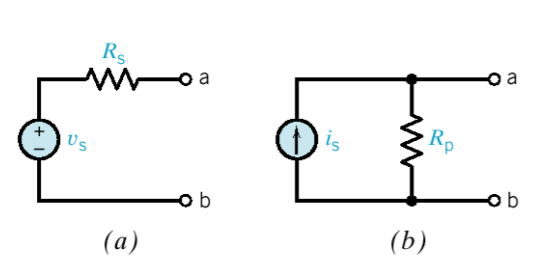
a,b는 둘다 open curcuit이므로, 전류가 흐르지 않는다. 따라서 a를 b의 형태로 변환하여도, 두 저항 $R_s= R_p$라고 본다.
(조금더 풀어쓰면 a라는 직렬연결 회로를 b라는 병렬 연결로 변환을 해주는 변환이라고 나는 이해했다. 아닐 수도 있습니다! )
$R = 0$이면,
$i_s = \frac{v_s}{R_s}$
$R = \infin$일때
$v_s = i_sR_p$를 만족한다.
위의 두 정리에 의하여 $R_p = R_s$가 되게 된다.

Superposition (중첩의 원리)

$i_1 => v_1$
$i_2 => v_2$
$i_1 + i_2= v_1 + v_2$을 만족하면 linear하다. 이를 이용하여
독립 전원이 있을 경우 ,mesh나 노드에 KCL을 적용하는 것이 아닌, 독립 전원을 키고 꺼서 linear conbination으로 구할 수 있다.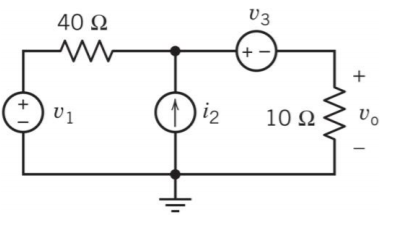
위의 식에서 각각의 독립 전원 하나씩을 키고 꺼서 식을 구한다.
독립 전원을 키고 끈다는 것의 의미는 독립 전압원일 경우, 전선을 연결한다고 받아들이고, 독립 전류원일 경우 선이 없다고 가정한다.

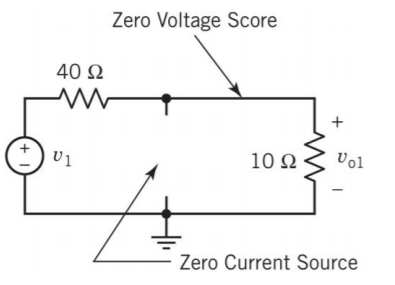
• $v_1$만 남겼을 경우의 식을 구하고 ,
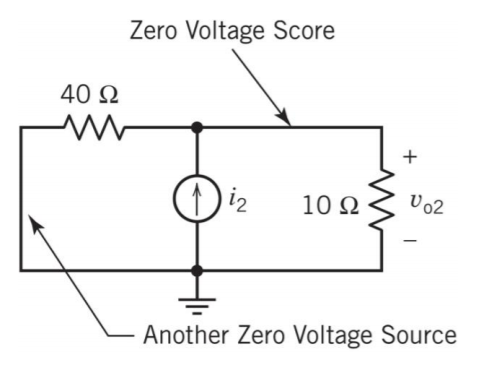
• $i_2$독립 전류원만 있을 때를 구하고,
  
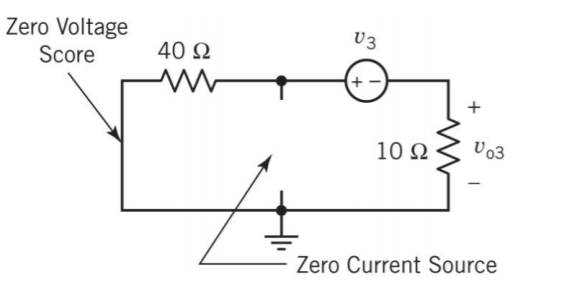
• $v_3$만 존재할 때의 식을 구해서 나온 식을 모두 더하면 해석할 수 있다.

Thevenin's Theorem

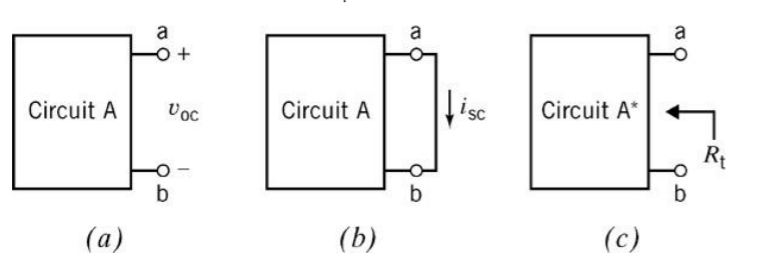
curcit이 다음과 같이 존재할 때, $R_t = \frac{v_{oc}}{i_{sc}}$를 만족한다. 즉, Circuit A에 2개의 경우만 구하면 나머지 하나는 위의 식을 통해 알아낼 수 있다.