멀쩡한 사각형

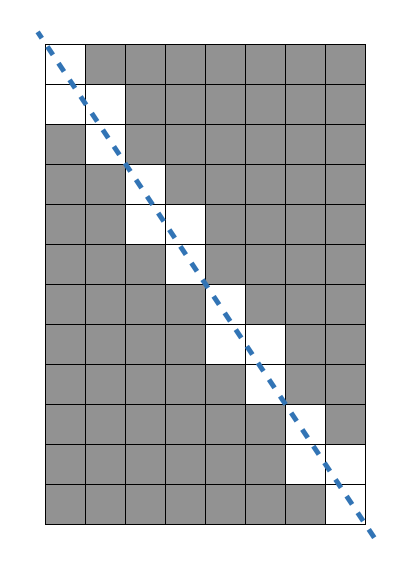
💣 문제

가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다. 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상태이기 때문에, 이 종이에서 원래 종이의 가로, 세로 방향과 평행하게 1cm × 1cm로 잘라 사용할 수 있는 만큼만 사용하기로 하였습니다.
가로의 길이 W와 세로의 길이 H가 주어질 때, 사용할 수 있는 정사각형의 개수를 구하는 solution 함수를 완성해 주세요.

https://programmers.co.kr/learn/courses/30/lessons/62048

💬 내 접근 방식

못 풀었다. 하나의 테스트케이스에서 시간초과가 계속 나더라. 내 접근 방식이다.

1. 선을 하나의 직선으로 생각
2. y 좌표를 계속해서 더해준다.

   for x in range(1, w):
       y = slope * x + h
       temp += int(y)

3. 다수 케이스 시간초과 => O(N)인 연산 횟수를 줄여야겠다.
4. 직선이 점을 지날 때, 겹치는 사각형이 반복적으로 나타나는구나 => gcd를 사용해서 나눠야겠다.
5. 유클리드 호제법으로 gcd를 찾고 나눈 값으로 진행한다.

   for x in range(1, int(w / gcd)):
   	y = slope * x + h / gcd
       temp += int(y)

6. 하나의 케이스에서 시간초과 발생

내가 생각할 땐, gcd가 1인 케이스에서 시간초과가 나는거 같은데, 확인할 방법은 없다. c언어로 풀이를 했으면 돌아갈까라는 생각이 들긴한다.

💯 확인한 풀이

조금 아쉬운 풀이였다. gcd로 사각형의 크기를 줄이고 진행했을 때, 겹치는 사각형은 $w/gcd + h/gcd -1$이라는 공식을 사용하면 된다고 한다. 예를 들어 $2\times3$ 사각형의 겹치는 부분은 $2 \times 3-1= 5$ 라는 것. 조금 더 재밌는 풀이가 있을 줄 알았는데 아쉽다.