[Mathematics] Haversine Formula

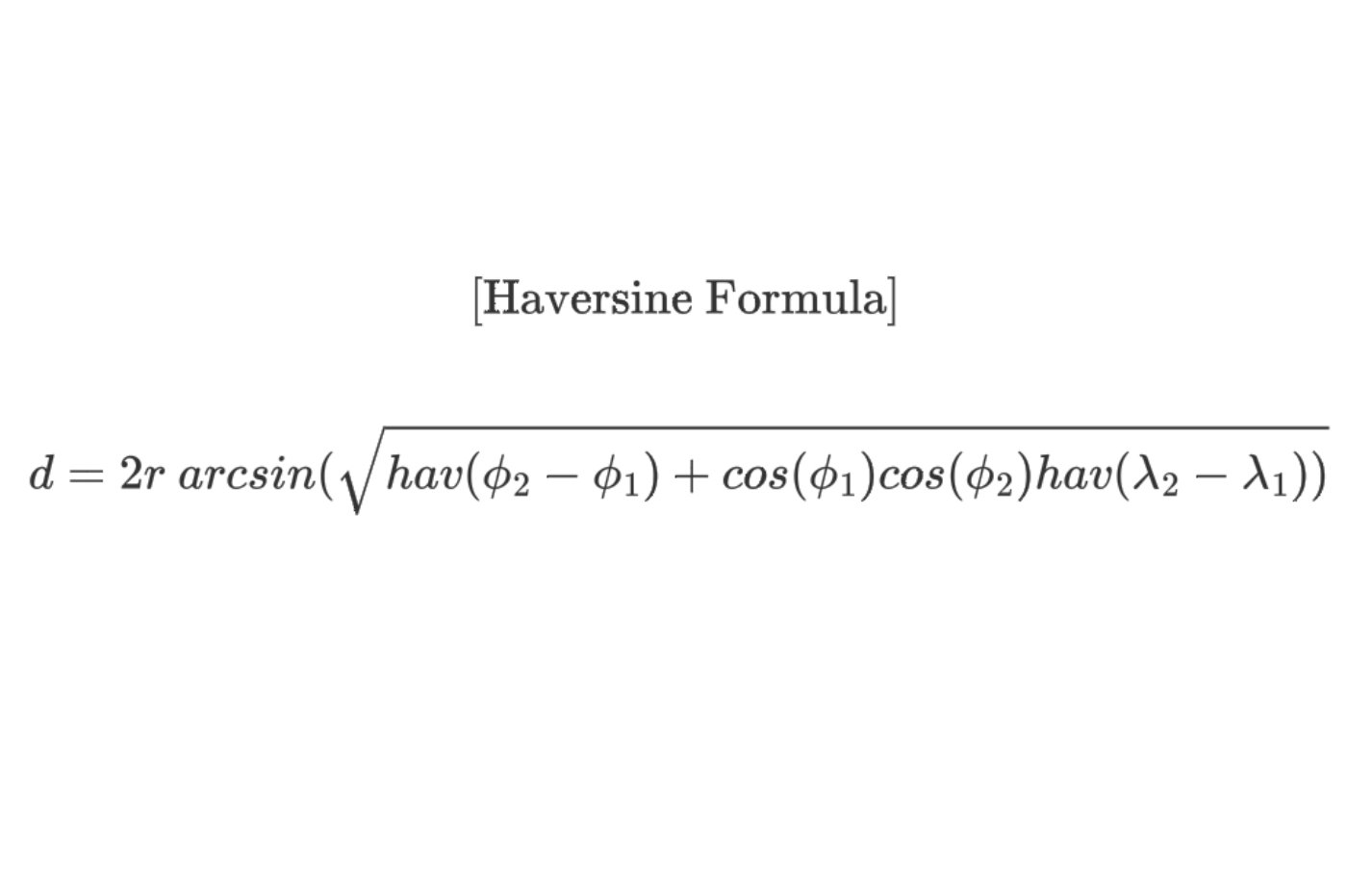
개요

gourmet-service 프로젝트를 개발하면서 지리 데이터를 건드릴 일이 생겼다.
Domain(Entity) 클래스에 지리 정보가 포함되게 되어, Geospatial이라는 지리 데이터 클래스를 구현하게 된 것.
위도, 경도, 그리고 선택적으로 고도를 통해 기술된 두 위치 사이의 최단 거리를 계산하는 로직이 필요했다.

구면에서의 거리 구하기

지구는 평면이 아니기 때문에, 단순 사칙연산만으로는 두 점 사이의 최단 거리를 구할 수 없다.
구면에서 두 점 사이의 최단 거리를 Greate-circle Distance(이하, 대원 거리)라고 부르는데, 이를 구하면 최단 거리의 근사값을 얻을 수 있다.

이를 구하는 방법으로는 Haversine Formula라는 공식이 있다.

Haversine Formula

위도와 경도로 기술된, 구면 좌표계 상의 두 점 사이의 대원 거리를 구하는 공식.

우선, 호의 중심각에 대한 수식을 보자.

다음으로는, 두 점의 위도와 경도로부터 중심각의 Haversine1을 구하는 수식을 보자.

Haversine은 그 이름에서 알 수 있듯이 Versine2의 절반을 계산하는 삼각함수이다.
그에 따라, Haversine 함수는 아래와 같이도 표현될 수 있다.

[수식 1] 과 [수식 3]을 가지고 중심각의 Haversine으로부터 두 점 사이의 대원거리를 구하는 수식을 만들어보자.

최종적으로 [수식 4]의 h에 [수식 2]를 대입하면, 두 점의 위도와 경도로부터 대원거리를 구할 수 있게 된다.

고도를 포함시키기

위치 정보에 고도가 포함되어 있는 경우, 이에 대한 거리도 고려해야 한다.

처음에는 구면 좌표계와 직교 좌표계 사이를 오가면서 좌표 변환을 해주어야 하나 머리를 싸맸는데... 생각해보니 그럴 필요가 없다.

이미 우리는 대원 거리를 구했으므로, 이를 통해 위도, 경도, 고도를 통해 기술된 두 위치를 아래와 같이 표현할 수 있다.

이제, P0와 P1사이의 유클리디안 거리3를 구하면 된다.

구현 방법

typealias Degree = Double
typealias Radian = Double
fun Degree.toRadian(): Radian = (this / 180 * PI)
fun Radian.toDegree(): Degree = (this * 180 / PI)
fun haversineFormula(x1: Double, y1: Double, x2: Double, y2: Double): Double {
    val haversineFunction: (Double) -> Double = { radian -> ((1 - cos(radian)) / 2) }
    val earthRadius: Double = 6372.8
    val latDelta = (x2 - x1).toRadian()
    val lonDelta = (y2 - y1).toRadian()
    val latDeltaHav = haversineFunction(latDelta)
    val lonDeltaHav = haversineFunction(lonDelta)
    val sqrtResult = sqrt(
        latDeltaHav +
            cos(x1.toRadian()) *
            cos(x2.toRadian()) *
            lonDeltaHav
    )
    return 2 * earthRadius * asin(sqrtResult)
}
fun haversineWithAltitude(x1: Double, y1: Double, z1: Double, x2: Double, y2: Double, z2: Double): Double {
    return sqrt(haversineFormula(x1, y1, x2, y2).pow(2) + ((z2 / 1000) - (z1 / 1000)).pow(2))
}

Haversine Formula의 모든 각 단위는 라디안 단위임을 명심하자.
또, 대다수의 지리 데이터에서 고도는 미터 단위라는 것에 유의하며, 단위 변환을 잘 해주자.

earthRadius값은 지구의 평균 반지름으로, Haversine Formula에서는 지구가 완전한 구라고 가정하고 계산하게 된다.

구현 검증

구현 검증 - 가까운 거리

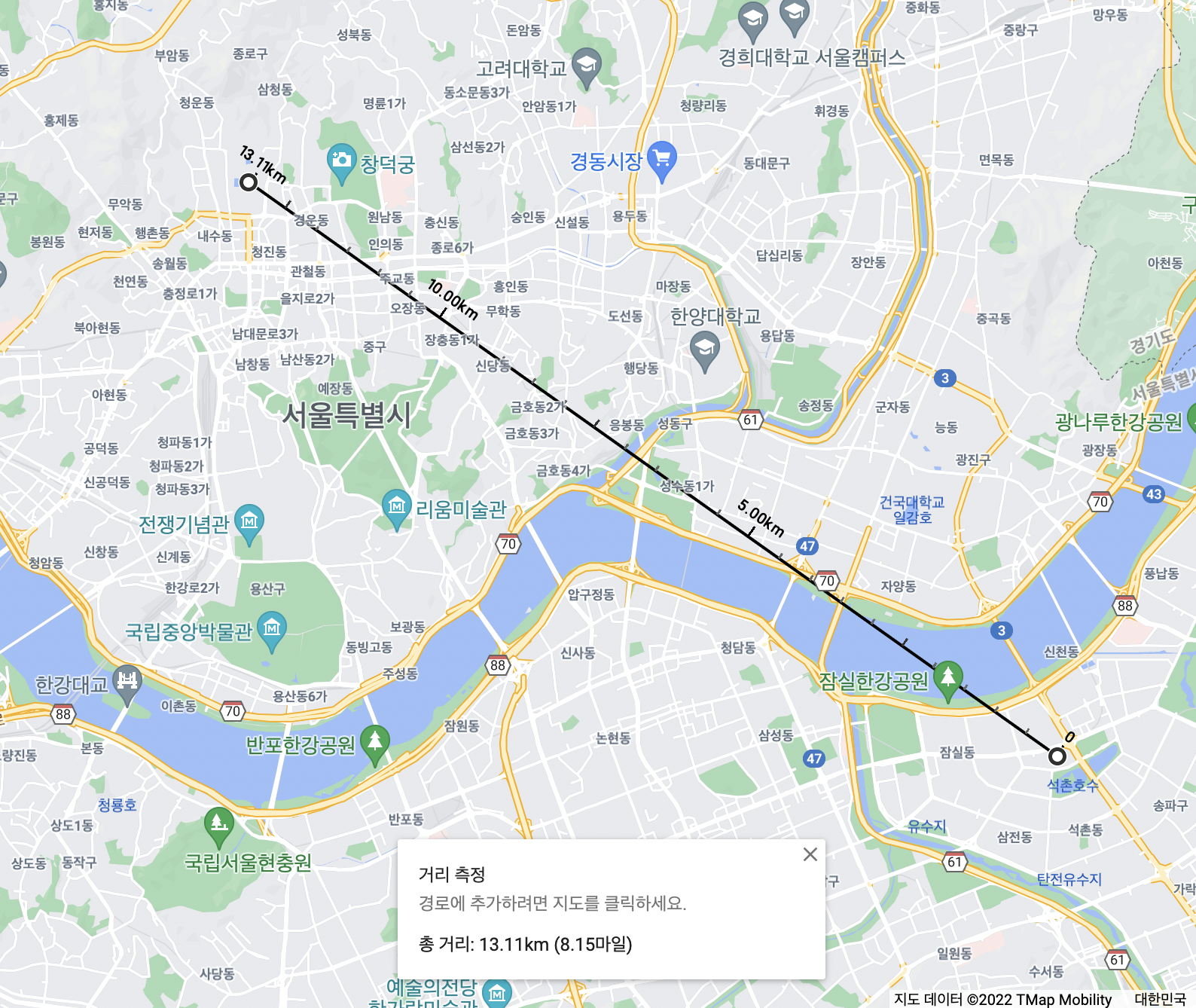
경복궁(37.57972629472382, 126.97703995428492)과 롯데월드(37.51132003130456, 127.09819918422973) 사이의 거리를 측정해보자.

Google Map으로 측정한 거리

Haversine Formula로 계산한 거리

• Haversine Distance: 13.116976136232822
• 오차: 0.00km

경복궁의 고도를 0km, 롯데월드의 고도를 3km로 설정하고 계산한 거리

• Altitude Distance: 13.455670290197412
• 오차: 0.01km

구현 검증 - 도시간 거리

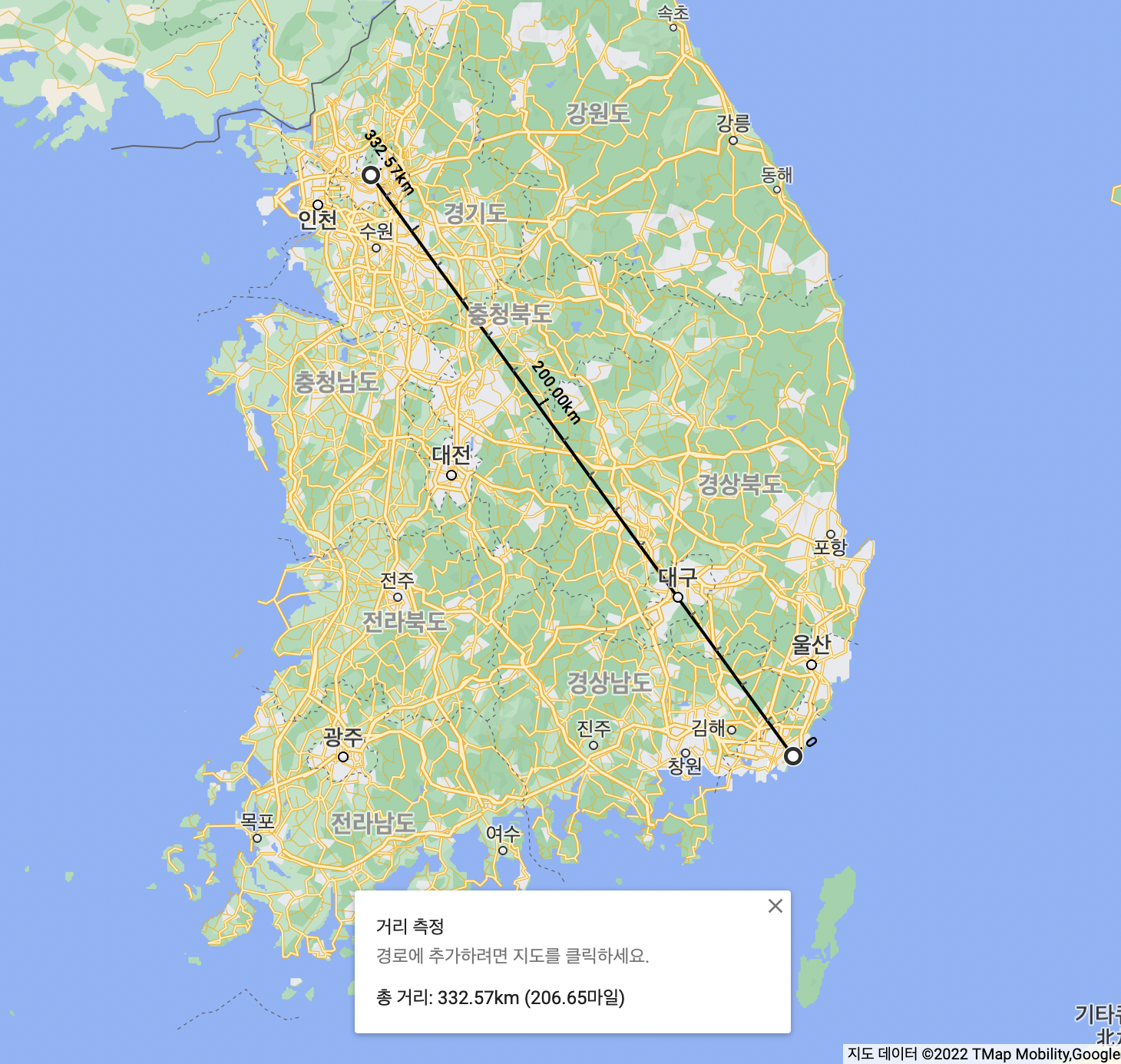
경복궁(37.57972629472382, 126.97703995428492)과 해운대(35.158853203095845, 129.16041116961833) 사이의 거리를 측정해보자.

Google Map으로 측정한 거리

Haversine Formula로 계산한 거리

• Haversine Distance: 332.753056608918
• 오차: 0.18km

구현 검증 - 대륙간 거리

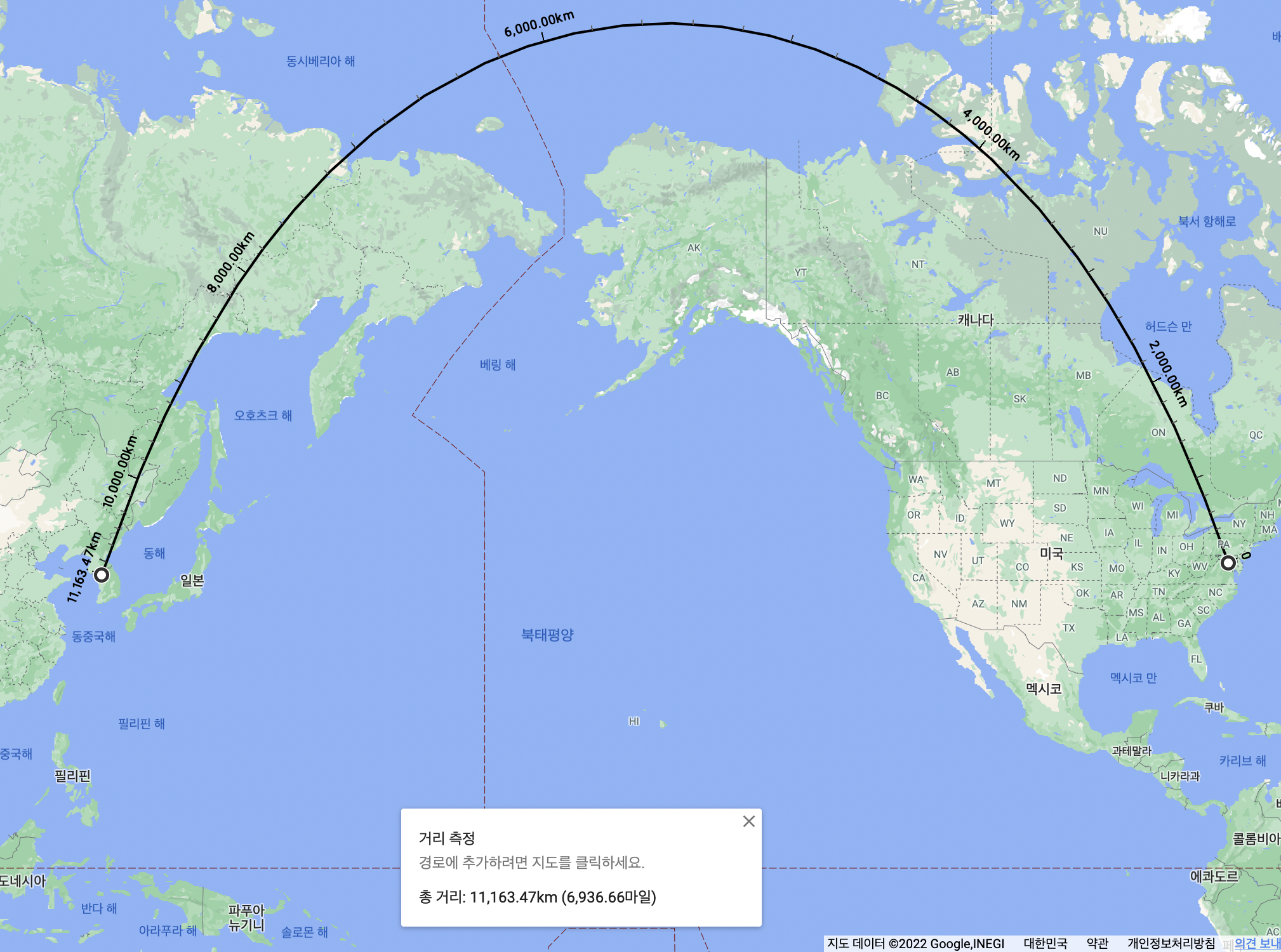
경복궁(37.57972629472382, 126.97703995428492)과 백악관(38.89803328255308, -77.03623996849913) 사이의 거리를 측정해보자.

Google Map으로 측정한 거리

Haversine Formula로 계산한 거리

• Haversine Distance: 11166.620281224583
• 오차: 3.15km

마치며

아무래도 지구를 완전한 구형으로 가정하고 계산을 하다 보니, 두 점 사이의 거리가 엄청나게 멀 경우에는 유의미한 계산 오차가 발생하게 된다.
더 정확한 거리 측정을 위해서는, 회전 타원체 상의 두 점 사이 거리를 계산하는 Vincenty's formulae4라는 공식을 사용하면 된다.

다만, Vincenty's formulae는 Haversine Formula에 비해 계산이 압도적으로 복잡한 것이 단점.

일반적인 경우에는 Haversine Formula를 쓰는게 무난하나, 위치가 멀거나 정확도가 중요한 경우에는 Vincenty's formulae를 쓰자.

---

Footnotes

[1]: 삼각함수의 일종, hav(x)와 같이 쓰인다. (상세 설명은 4번 출처, "Versine"을 참고)
[2]: 삼각함수의 일종, versin(x)와 같이 쓰인다. (상세 정보는 4번 출처, "Versine"을 참고)
[3]: 피타고라스 정리와 같아 보일텐데, 실제로 유클리디안 거리는 피타고라스 정리의 응용이다.
[4]: 추후, 별도 문서로 작성 예정.

---

References

1. "Great-circle distance" by "Wikipedia"
2. "Central angle" by "Wikipedia"
3. "Haversine formula" by "Wikipedia"
4. "Versine" by "Wikipedia"
5. "Euclidean distance" by "Wikipedia"
6. "Vincenty's formulae" by "Wikipedia"

---