📌 최적 부분 구조 (Optimal Substructure)
📝 동적 계획법의 조건
- 최적 부분 구조(Optimal Substructure)
- 중복되는 부분 문제(Oberlapping Subproblems)
최적 부분 구조가 있다는 건 부분 문제들의 최적의 답을 이용해서 기존 문제의 최적의 답을 구할 수 있다는 걸 의미한다.
ex) 피보나치 수
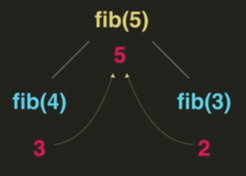
ex) 최단 경로 찾기
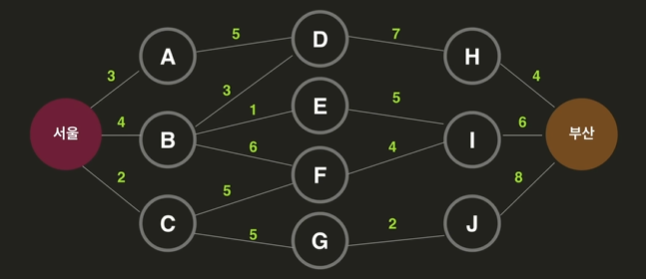
부산으로 가기 위해서는 H, I, J를 반드시 거쳐가야 한다.
서울에서 H, 서울에서 I, 서울에서 J로 가는 최단 경로 문제를 풀어야 한다.
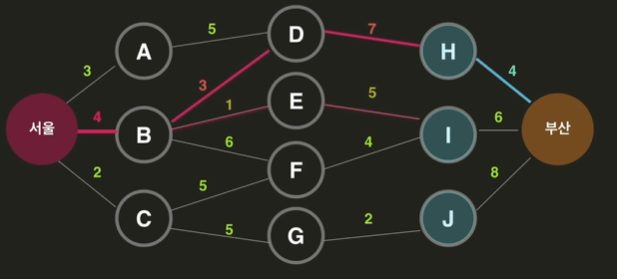
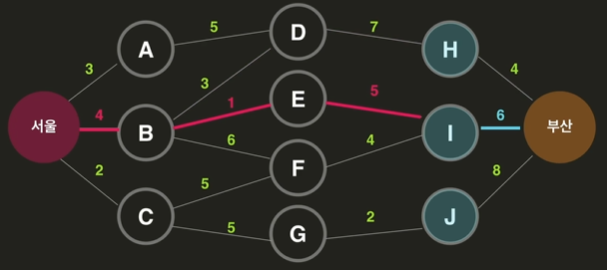
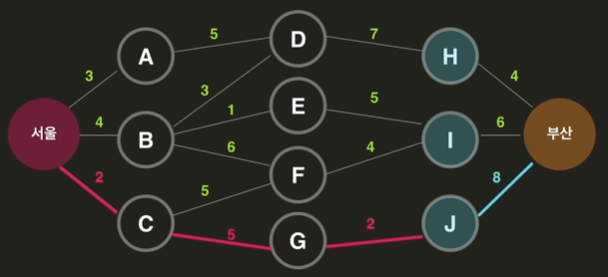
위의 세 가지를 비교해보면 서울-부산의 최단 경로를 알 수 있다.
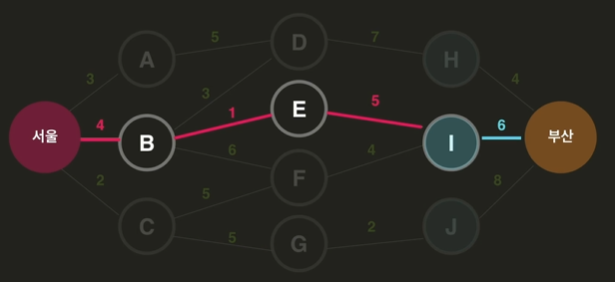
📌 중복되는 부분 문제(Overlapping Subproblems)
ex) 피보나치 수
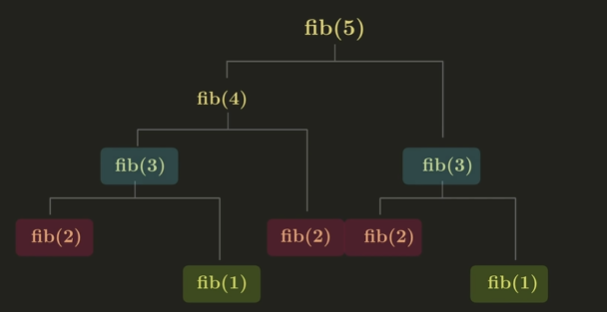
중복되는 부분 문제들이 존재한다.
이렇게 중복되는 부분 문제들을 여려 번 계산하는 건 비효율적이다.
이 문제를 해결하는 게 동적 계획법(Dynamic Programming)이다.
그러나 문제를 부분 문제로 나눈다고 해서 항상 중복되는 부분 문제가 있는 것은 아니다. 예를 들어서 분할 정복을 사용하는 합병 정렬을 보자.
merge-sort ([16, 11, 6, 13, 1, 4, 10, 7])8개의 리스트를 합병 정렬하려면 우선 4개의 리스트 두 개 [16, 11, 6, 13], [1, 4, 10, 7]로 나눈다. 그리고 각 리스트를 각각 합병 정렬 한다. 왼쪽 리스트를 부분 정복하는 것과 오른쪽 리스트를 부분 정복하는 것은 서로 독립적이다. 따라서 합병 정렬은 중복되지 않는 부분 문제(Non=overlapping Subproblem)이라고 한다.
📌 동적 계획법
최적 부분 구조가 있다는 것은 부분 문제들의 최적의 답을 이용해서 기존 문제를 풀 수 있다. 기존 문제를 부분 문제로 나눠서 풀다보면 중복되는 부분 문제들이 있을 수도 있다. 똑같은 문제를 여러 번 풀게되는 비효율이 발생되게 된다. 이 문제를 해결하기 위해 사용하는 방법이동적 계획법(Dynamic Programmaing)이라고 한다.
- 최적 부분 구조가 있다.
- 중복되는 부분 문제들이 있다
위의 경우 동적 계획법(Dynamic Programmaing)으로 문제를 해결한다.
동적 계획법(Dynamic Programmaing)이란 한 번 계산한 결과를 버리지 않고 재활용하는 방식을 의미한다.
ex) 피보나치 수
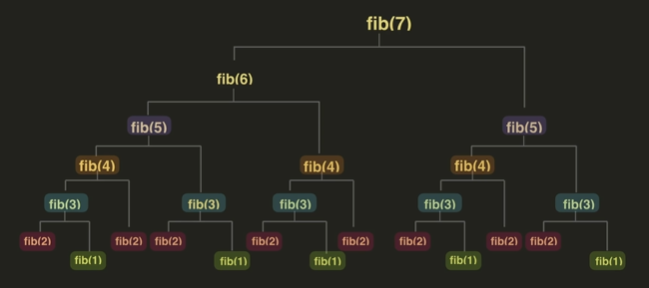
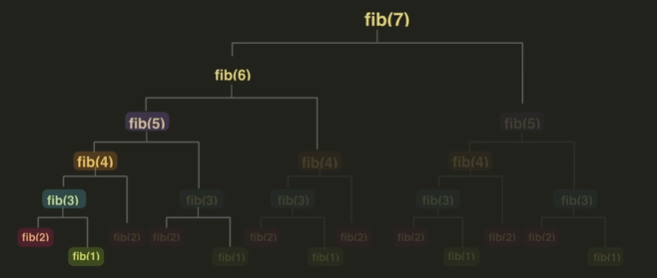
중복되는 부분 문제들을 각각 딱 한 번씩만 풀자는 게 동적 계획법의 취지이다.
동적 계획법을 구현하는 방법은 두 가지가 있다.
- Memoization
- Tabularion
📌 Memoization
중복되는 계산은 한 번만 계산 후 메모하는 방식을 Memoization이라고 한다.
Memoization 방법은 하향식 접근(Top-down Approach)이라고도 한다.
ex) 피보나치 수
한 번 계산한 값을 담아놓을 딕셔너리를 만든다. 이처럼 다시 사용할 값들을 저장해놓는 공간을 cache라고 한다.
6번째 피보나치 수를 찾는다고 가정하자.

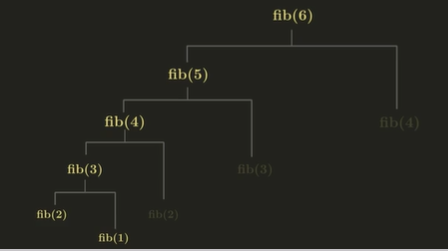
fib(2)는 base case이므로 답을 바로 알 수 있다. 다음 번에 fib(2)를 또 사용하게 될지도 모르니 이를 딕셔너리 cache에 담아두도록 하자.
fib(1)도 base case이므로 답을 바로 알 수 있다. fib(1)의 값도 cache에 기록해둔다.
fib(2)와 fib(1)을 알게되었으므로 fib(3)도 계산할 수 있다. fib(3)의 결과값도 cache에 기록해둔다.
fib(2)는 이미 cache에 담겨 있으므로 cache에서 값을 가져와 사용한다.
fib(3)과 fib(2)를 통해 fib(4)도 계산할 수 있고 이 값을 cache에 기록한다.
fib(3)은 cache에 담겨 있으므로 값을 가져와 사용하면 fib(5)도 계산할 수 있고 cache에 기록해둔다.
반대편의 fib(4)는 cache에서 값을 가져와 사용할 수 있다.
fib(5)와 fib(4)를 이용하여 fib(6)을 계산할 수 있다.
각 부분 문제를 한 번씩만 풀어서 중복되는 부분 문제에 대한 비효율성을 해결했다.
✅ 피보나치 수열(Memoization)
n번째 피보나치 수를 찾아주는 함수 fib_memo을 작성하라.
fib_memo는 반드시 memoization 방식으로 구현해야 한다.
💻 풀이
def fib_memo(n, cache):
if n <= 2:
return 1
if n in cache:
return cache[n]
cache[n] = fib_memo(n-1, cache) + fib_memo(n-2, cache)
return cache[n]
def fib(n):
fib_cache = {}
return fib_memo(n, fib_cache)
print(fib(10))
print(fib(50))
print(fib(100))👉 결과
55
12586269025
354224848179261915075❗ 딕셔너리[key] = value
📌 Tabulation
이번에는 중복되는 것 부터 푸는 Tabulation에 대해 알아보자.
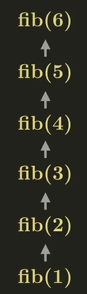
fib(1) -> fig(2) -> fib(3) -> fib(4) -> fib(5) -> fib(6)
아래에서 위로 올라가는 상향식 접근(Bottom-up Approach)이라고 한다.
이 방식으로 하면 당연히 중복되는 과정이 없어진다.
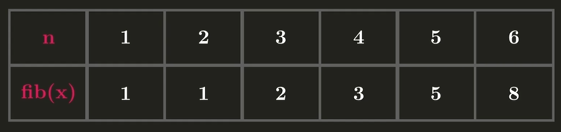
Tabulation은 Table 방식으로 정리한다는 뜻이다.
📝 Memoization vs Tabulation
Memoization은재귀를 사용한다.Tabulation은반복문을 사용한다.
✅ 피보나치 수열(Tabulation)
n번째 피보나치 수를 찾아주는 함수 fib_tab을 작성하라.
fib_tab는 반드시 tabulation 방식으로 구현하셔야 한다.
💻 풀이
def fib_tab(n):
fib_table = [0, 1, 1]
for i in range(3, n+1):
fib = (fib_table[i-1] + fib_table[i-2])
fib_table.append(fib)
return fib_table[n]
print(fib_tab(10))
print(fib_tab(56))
print(fib_tab(132))👉 결과
55
225851433717
1725375039079340637797070384... ing
