[백준 파이썬] 1005 ACM Craft

백준 1005

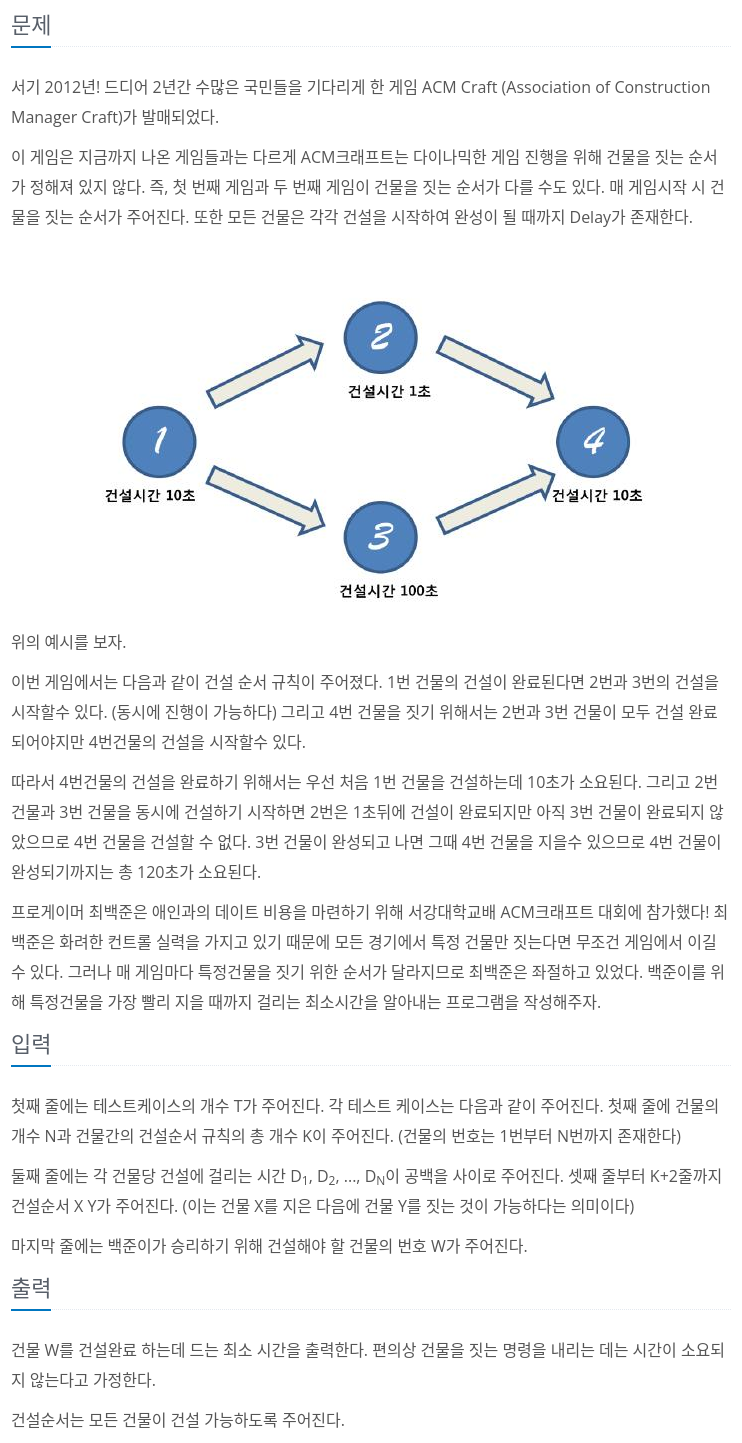
백준 2252번 문제와 같은 유형의 위상 정렬 문제이다. 차이점은 진입 차수가 0일 때 큐에 추가하는 것 뿐만 아니라 선행 노드에 걸리는 시간이 최대인 값으로 업데이트 시켜줘야한다.
인접 리스트와 진입 차수 배열, 걸린 시간을 저장하기 위한 또 다른 배열이 필요하다.
이 문제에서 진입 차수 배열은 현재 건물을 짓기 위해 건설해야하는 남은 건물 수로 볼 수 있다.

from collections import deque

T = int(input())
for _ in range(T):
    N, K = map(int, input().split())
    D = [0] + list(map(int, input().split()))
    X_Y = [list(map(int, input().split())) for _ in range(K)]
    target = int(input())

    graph = [[] for _ in range(N+1)] # 인접 리스트 초기화
    in_degree = [0 for _ in range(N+1)] # 진입 차수 배열 초기화
    times = [0 for _ in range(N+1)] 시간 저장용 배열 초기화

    for x, y in X_Y:
        graph[x].append(y)
        in_degree[y] += 1 # 진입 차수 카운트

	# 노드의 진입 차수가 0이라면 해당 노드를 큐에 추가
    q = deque()
    for i, n in enumerate(in_degree[1:], 1):
        if n == 0:
            q.append(i)

    while q:
        build = q.popleft()
        for next_build in graph[build]:
        	# 다음 건설까지 필요한 시간은 `이때까지 걸린 시간 + 현재 건물을 짓는데 필요한 시간`의 최댓값이다.
            times[next_build] = max(times[next_build], times[build]+D[build])
            in_degree[next_build] -= 1 # 선행되어야 하는 건물 완성
            if in_degree[next_build] == 0: # 선행 되어야 하는 건물이 모두 완성되었다면
                q.append(next_build) # 리스트에 추가

    print(times[target] + D[target]) # 마지막 타겟 건물에 필요한 시간 추가