[백준 파이썬] 1654 랜선 자르기

백준 1654

import sys
input = sys.stdin.readline

K, N = map(int, input().split())
lans = [int(input()) for _ in range(K)]

# 탐색의 시작 지점과 끝 지점을 정해준다
start, end = 1, max(lans)

while start <= end:
    mid = (start + end) // 2
    # 자르고 난 랜선의 수는 몫들의 합으로 표현할 수 있다.
    lan = sum([length//mid for length in lans])

	# 랜선의 수가 너무 많다면 너무 짧게 잘랐다 -> 시작 지점을 키워준다.
    if lan >= N:
        start = mid + 1
    # 그게 아니라면 너무 길게 잘랐으므로 끝 지점을 줄여준다.
    else:
        end = mid - 1

print(end)

랜선을 잘랐을 때 N개의 랜선을 만드는데 랜선의 길이를 최대로 해야한다. 이런 문제는 이분 탐색으로 답을 찾을 수 있다.
이분 탐색에서는 탐색의 시작 지점과 끝 지점을 잘 지정해두어야한다. 문제에서 답이 나올 수 있는 범위보다 작게 설정하면 답이 안나오는 경우가 생긴다.

이 문제의 경우
예제 입력 1:
4 11
802
743
457
539
일 때 랜선을 11개로 잘랐을 때 길이의 최대값을 찾는 과정이다.

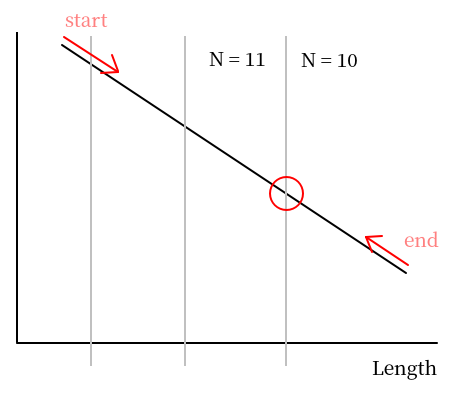
이런 느낌으로 start와 end 사이 mid를 수정해가면서 최대 또는 최솟값을 찾아나간다고 보면 된다.
시작점과 끝 지점을 수정하는 조건문에서 범위나 start, mid, end 어떤걸 출력해야 할지 헷갈리는 경우가 많다.
위에 그래프와 이분 탐색 반복문의 조건을 보면 while start <= end:에서 start와 end가 엇갈릴 때 반복문이 종료 된다. 그래프처럼 두 값의 중간값으로 잘라주는 값을 수정하고 점점 목표로 하는 값에 가까워진다. 반복문마다 start와 mid, end, 랜선의 수를 출력해 보면

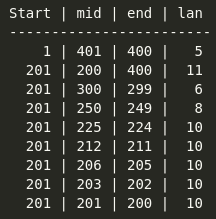
이렇게 나타나는데 마지막 출력을 보면 시작점과 끝 지점이 엇갈려있고 lan의 수가 목표로 하는 숫자보다 1개 적게 나타난다. 이 결과와 그래프부터 start는 N=10일 때 랜선 길이의 최솟값, end는 N=11일 때 랜선 길이의 최댓값이 되는 것을 확인할 수 있다.