[Algorithm/Programmers] 자바 - 정수 삼각형

문제	플랫폼	난이도	유형	풀이 링크	문제 링크
정수 삼각형	Programmers	Level 3	DP	풀이	문제

풀이

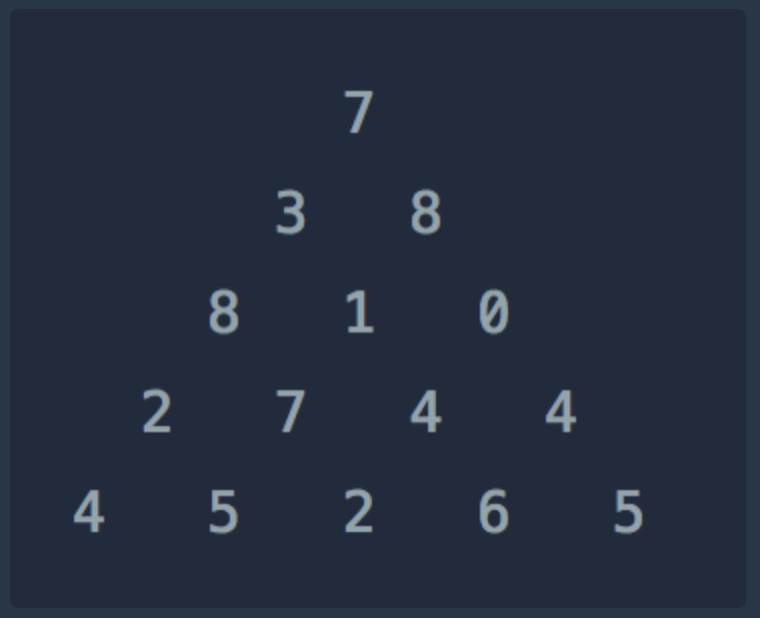
주어진 정수로 이루어진 삼각형의 꼭대기에서 최하단까지
좌, 우 한 칸씩 이동하며 합한 수의 최댓값을 구하는 문제입니다.

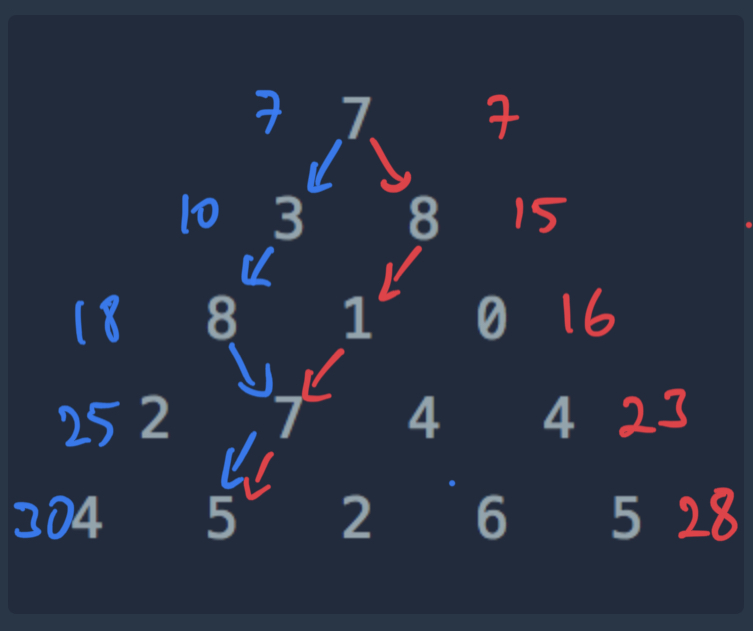
두 가지 예시처럼 아래로 내려오며 각 지점의 정수를 합하여 최하단에 도착한 합들의 경우의 수 중에서 최댓값을 구하면 됩니다.

파란색처럼 내려오는 경우가 최댓값이 되는 경우의 수입니다.
이렇게 찾은 최댓값을 반환하면 되는 문제입니다.

높이가 최대 500 입니다.
효율성 없이 풀면 무조건 터질 것 같습니다.

Case 1 : DFS

private void dfs(int r, int c, int sum) {

    if (r == len - 1) {
        maxSum = sum > maxSum ? sum : maxSum;
        return;
    }

    dfs(r + 1, c, sum + triangle[r + 1][c]);
    dfs(r + 1, c + 1, sum + triangle[r + 1][c + 1]);

}

무지성 DFS를 해보니 역시 자비없는 시간초과를 받았습니다.
DFS를 할 경우 완전탐색을 하게 되는데, 이는 지수 시간 복잡도를 가집니다. O(2^N)

Case 2 : DP

이 문제는 꼭대기부터 바닥까지 내려가며 정수의 합 중 가장 큰 값을 구하는 것입니다.

DP로 생각해면,
큰 문제를 작은 문제로 쪼개어야 합니다.

결국, 각 층, 각 칸에 대환 최대값을 구하면 됩니다.

따라서, 점화식은 다음과 같을 것입니다.

dp[i][j] = triangle[i][j] + 상단(이전 row) 좌/우 중 최댓값

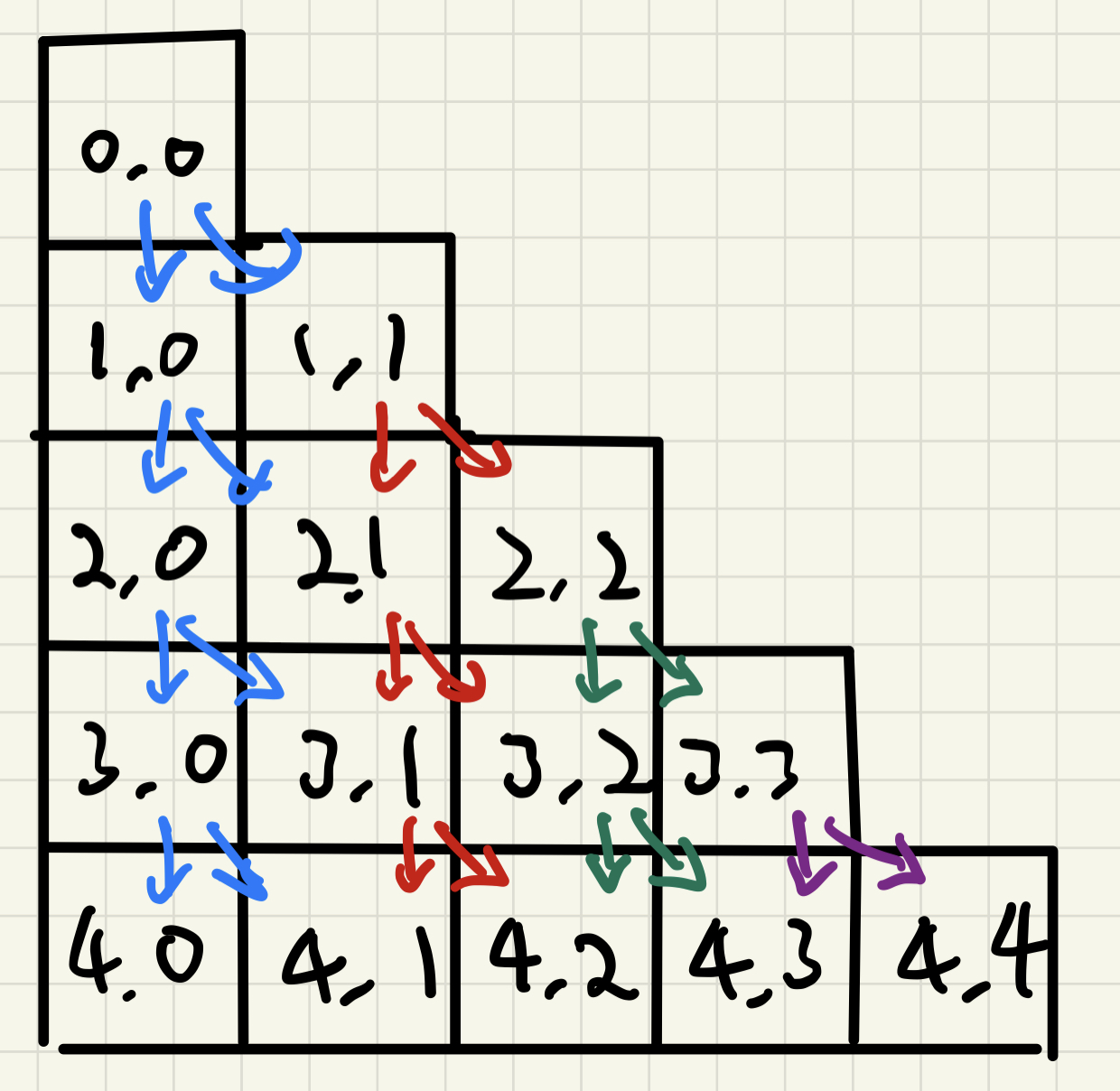
꼭대기 칸을 제외한 나머지 칸은 해당 칸으로 올 수 있는 칸이
상단 2칸 (row - 1, col - 1 || col) 있습니다.
단, col == 1 인 칸은 (row -1, col) 입니다.
각 칸에 대한 최댓값은 해당 칸 + 이전 두 칸 중 최댓값 입니다.
꼭대기부터 바닥까지 순차적으로 각 칸의 최댓값을 적어 나가기 때문에 그렇습니다.

점화식으로 각 칸에 대하여, 가질 수 있는 최댓값을 구하며 마지막 층까지 계산하면 되는 문제입니다.

DP를 사용하면, O(N^2)에 해결이 가능하게 됩니다.

private int dp(int[][] triangle, int len) {
    int[][] dp = new int[len][len];
    dp[0][0] = triangle[0][0];

    int max = Integer.MIN_VALUE;

    for (int i = 1; i < len; i++) {

        dp[i][0] = triangle[i][0] + dp[i - 1][0];

        for (int j = 1; j < i + 1; j++) {
            dp[i][j] = triangle[i][j] + Math.max(dp[i - 1][j - 1], dp[i - 1][j]);
        }
        
    }

    for (int i = 0; i < dp[dp.length - 1].length; i++) {
        max = Math.max(dp[dp.length - 1][i], max);
    }

    return max;
}

Case 3 : DP 상위 풀이

private int dp(int[][] triangle, int len) {
    for (int i = 1; i < len; i++) {
        triangle[i][0] += triangle[i - 1][0];
        triangle[i][i] += triangle[i - 1][i - 1];

        for (int j = 1; j < i; j++)
            triangle[i][j] += Math.max(triangle[i - 1][j - 1], triangle[i - 1][j]);
    }

    return Arrays.stream(triangle[len - 1]).max().getAsInt();
}

프로그래머스 상단에 있는 풀이입니다.
굉장히 직관적이고 효율적으로 깔끔한 코드 같습니다.