LCS 알고리즘은 문자열 관련 알고리즘 중 하나로 보통 최장 공통 부분 수열의 의미하나 최장 공통 문자열을 가리키기도 한다
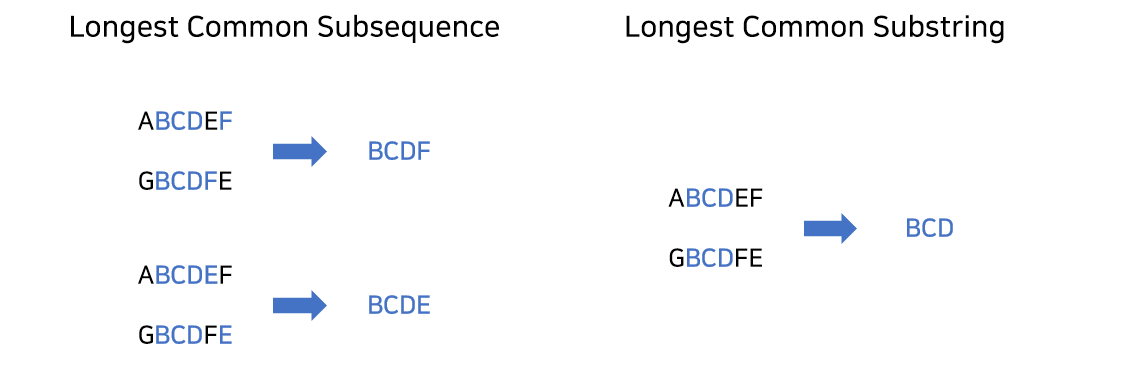
Longest Common SubSeqeunce(최장 공통 부분 수열)- 위 사진에서 최장 공통 부분수열은 BCDF, BCDE가 될 수 있다.
- 부분수열이기 때문에 문자 사이를 건너뛰어 공통되면서 가장 긴 부분 문자열을 찾으면 된다.
Longest Common SubString(최장 공통 문자열)- 위 사진에서 최장 공통 문자열은 BCD입니다.
- 부분문자열이 아니기 때문에 한번에 이어져있는 문자열만 가능하다.
알고리즘 개념은 이 글에서 매우 잘 설명해주기 때문에 해당 포스팅의 설명을 읽어보면 좋다 사실 이 포스팅보다 더 이해하기 쉽게 쓸 자신이 없다
해당 알고리즘의 기본 코드는 아래와 같다.
X = "ABCDEF"
Y = "GBCDFE"
def longest_common_subString(X, Y): # 최장 공통 문자열
dp = [[0] * (len(Y) + 1) for _ in range(len(X) + 1)]
for i in range(1, len(dp)):
for j in range(1, len(dp[0])):
if Y[i - 1] == X[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = 0
mx = 0 # dp 최댓값 찾기
for i in range(1, len(dp)):
tmp_mx = max(dp[i])
mx = max(mx, tmp_mx)
return mx
def longest_common_subSeqeunce(X, Y): # 최장 공통 부분수열
dp = [[0] * (len(Y) + 1) for _ in range(len(X) + 1)]
for i in range(1, len(dp)):
for j in range(1, len(dp[0])):
if Y[i - 1] == X[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
return dp[-1][-1]
print(longest_common_subString(X, Y))
print(longest_common_subSeqeunce(X, Y))참고로 longest_common_subSequence에서는 dp값 마지막 값을 바로 return 하면 되지만 longest_common_subString의 경우 dp 배열 내에서 최댓값을 찾는 과정을 거쳐야 함을 잊지 말자 !
+)
올해 코테에서 알고리즘 색이 짙은(?) 문제를 본 적이 거의 없어서 진짜 요즘 추세는 확실히 시뮬레이션(구현)이구나 생각했는데 최근 코테에서 통수 당했다.. 😅
유명한 알고리즘 유형들은 거의 암기하듯 손에 익혀두어야 할 것 같다 기본기에 충실하자
